Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Hà Tĩnh năm 2023. Đây là tài liệu vô cùng quan trọng giúp các em học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi sắp tới.
Chúng tôi đã tổng hợp đầy đủ các đề thi chính thức, đề thi thử từ các trường THCS trên địa bàn Hà Tĩnh, đảm bảo tính cập nhật và độ chính xác cao.
Câu 1: Rút gọn các biểu thức sau: a) \(A = \sqrt {48} - 3\sqrt 3 \). b) \(B = \left( {\frac{1}{{\sqrt x + 2}} + \frac{1}{{\sqrt x - 2}}} \right):\frac{{\sqrt x }}{{x - 4}}\) (với \(\left. {x > 0;x \ne 4} \right)\).
Câu 1: Rút gọn các biểu thức sau:
a) \(A = \sqrt {48} - 3\sqrt 3 \).
b) \(B = \left( {\frac{1}{{\sqrt x + 2}} + \frac{1}{{\sqrt x - 2}}} \right):\frac{{\sqrt x }}{{x - 4}}\) (với \(\left. {x > 0;x \ne 4} \right)\).
Câu 2:
a) Cho hai đường thẳng \(\left( {{d_1}} \right):y = (m - 3)x + 4\left( m \right.\) là tham số) và \(\left( {{d_2}} \right):y = 2x - 1\). Tìm giá trị của \(m\) để hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) song song với nhau.
b) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x - y = 3}\\{3x + 2y = 8}\end{array}} \right.\).
Câu 3: Cho phương trình \({x^2} - 2mx + {m^2} - m - 2 = 0\) (m là tham số). Tìm giá trị của m để phương trình đã cho có 2 nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(\frac{{{x_1}{x_2} + 1}}{{x_1^2 + x_2^2 + 2\left( {1 + {x_1}{x_2}} \right)}} = \frac{1}{6}.\)
Câu 4: Một phòng họp ban đầu có 96 ghế được xếp thành các dãy và số ghế trong mỗi dãy đều bằng nhau. Có một lần phòng họp phải cất bớt 2 dãy ghế và mỗi dãy còn lại xếp thêm 1 ghế (số ghế trong các dãy vẫn bằng nhau) để vừa đủ chỗ ngồi cho 110 đại biểu. Hỏi ban đầu trong phòng họp có bao nhiêu dãy ghế?
Câu 5: Cho tam giác ABC vuông tại A, đường cao AH (\(H \in BC\)). Biết độ dài đoạn \(AB = 5cm\) và \(AH = 4cm.\) Tính độ dài đoạn BH và diện tích tam giác ABC.
Câu 6: Cho tam giác ABC nhọn. Đường tròn (O) đường kính BC cắt các cạnh AB, AC lần lượt tại D và E (D khác B và E khác C). Gọi H là giao điểm của hai đường thẳng BE và CD.
a) Chứng minh ADHE là tứ giác nội tiếp.
b) Đường thẳng AH cắt BC tại F và cắt đường tròn (O) tại điểm P (P nằm giữa A và H). Đường thẳng DF cắt đường tròn (O) tại điểm K (K khác D). Gọi M là giao điểm của EK và BC, I là tâm đường tròn ngoại tiếp tam giác HDP. Chứng minh \(C{E^2} = BC.MC\) và ba điểm B, I, P thẳng hàng.
Câu 7: Cho a, b, c là các số thực khác không. Tim giá trị nhỏ nhất của biểu thức:
\(P = \frac{{{a^2}}}{{{a^2} + 2{{(b + c)}^2}}} + \frac{{{b^2}}}{{{b^2} + 2{{(c + a)}^2}}} + \frac{{{c^2}}}{{{c^2} + 2{{(a + b)}^2}}}.\)
----- HẾT -----
Câu 1: Rút gọn các biểu thức sau:
a) \(A = \sqrt {48} - 3\sqrt 3 \).
b) \(B = \left( {\frac{1}{{\sqrt x + 2}} + \frac{1}{{\sqrt x - 2}}} \right):\frac{{\sqrt x }}{{x - 4}}\) (với \(\left. {x > 0;x \ne 4} \right)\).
Câu 2:
a) Cho hai đường thẳng \(\left( {{d_1}} \right):y = (m - 3)x + 4\left( m \right.\) là tham số) và \(\left( {{d_2}} \right):y = 2x - 1\). Tìm giá trị của \(m\) để hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) song song với nhau.
b) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x - y = 3}\\{3x + 2y = 8}\end{array}} \right.\).
Câu 3: Cho phương trình \({x^2} - 2mx + {m^2} - m - 2 = 0\) (m là tham số). Tìm giá trị của m để phương trình đã cho có 2 nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(\frac{{{x_1}{x_2} + 1}}{{x_1^2 + x_2^2 + 2\left( {1 + {x_1}{x_2}} \right)}} = \frac{1}{6}.\)
Câu 4: Một phòng họp ban đầu có 96 ghế được xếp thành các dãy và số ghế trong mỗi dãy đều bằng nhau. Có một lần phòng họp phải cất bớt 2 dãy ghế và mỗi dãy còn lại xếp thêm 1 ghế (số ghế trong các dãy vẫn bằng nhau) để vừa đủ chỗ ngồi cho 110 đại biểu. Hỏi ban đầu trong phòng họp có bao nhiêu dãy ghế?
Câu 5: Cho tam giác ABC vuông tại A, đường cao AH (\(H \in BC\)). Biết độ dài đoạn \(AB = 5cm\) và \(AH = 4cm.\) Tính độ dài đoạn BH và diện tích tam giác ABC.
Câu 6: Cho tam giác ABC nhọn. Đường tròn (O) đường kính BC cắt các cạnh AB, AC lần lượt tại D và E (D khác B và E khác C). Gọi H là giao điểm của hai đường thẳng BE và CD.
a) Chứng minh ADHE là tứ giác nội tiếp.
b) Đường thẳng AH cắt BC tại F và cắt đường tròn (O) tại điểm P (P nằm giữa A và H). Đường thẳng DF cắt đường tròn (O) tại điểm K (K khác D). Gọi M là giao điểm của EK và BC, I là tâm đường tròn ngoại tiếp tam giác HDP. Chứng minh \(C{E^2} = BC.MC\) và ba điểm B, I, P thẳng hàng.
Câu 7: Cho a, b, c là các số thực khác không. Tim giá trị nhỏ nhất của biểu thức:
\(P = \frac{{{a^2}}}{{{a^2} + 2{{(b + c)}^2}}} + \frac{{{b^2}}}{{{b^2} + 2{{(c + a)}^2}}} + \frac{{{c^2}}}{{{c^2} + 2{{(a + b)}^2}}}.\)
----- HẾT -----
Câu 1 (VD):
Phương pháp:
a) Căn bậc hai của một số \(a\) là một số \(x\) sao cho \({x^2} = a\)
b) Quy đồng và rút gọn sử dụng hằng đẳng thức.
Cách giải:
a) \(A = \sqrt {48} - 3\sqrt 3 \).
Ta có: \(A = \sqrt {48} - 3\sqrt 3 = \sqrt {{{3.4}^2}} - 3\sqrt 3 = 4\sqrt 3 - 3\sqrt 3 = \sqrt 3 \)
Vậy \(A = \sqrt 3 .\)
b) \(B = \left( {\frac{1}{{\sqrt x + 2}} + \frac{1}{{\sqrt x - 2}}} \right):\frac{{\sqrt x }}{{x - 4}}\) (với \(\left. {x > 0;x \ne 4} \right)\).
Với \(x > 0;x \ne 4\) ta có:
\(\begin{array}{l}B = \left( {\frac{1}{{\sqrt x + 2}} + \frac{1}{{\sqrt x - 2}}} \right):\frac{{\sqrt x }}{{x - 4}}\\\,\,\, = \left( {\frac{{\sqrt x - 2}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} + \frac{{\sqrt x + 2}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}} \right).\frac{{x - 4}}{{\sqrt x }}\\\,\,\, = \frac{{2\sqrt x }}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}.\frac{{x - 4}}{{\sqrt x }}\\\,\,\, = \frac{{2\sqrt x }}{{x - 4}}.\frac{{x - 4}}{{\sqrt x }}\\\,\,\, = 2\end{array}\)
Vậy \(B = 2.\)
Câu 2 (VD):
Phương pháp:
a) Để hai đường thẳng song song thì hệ số góc bằng nhau.
b) Sử dụng phương pháp thế hoặc phương pháp trừ vế.
Cách giải:
Cách giải:
a) Cho hai dường thẳng \(\left( {{d_1}} \right):y = (m - 3)x + 4\left( m \right.\) là tham số) và \(\left( {{d_2}} \right):y = 2x - 1\). Tìm giá trị của \(m\) để hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) song song với nhau.
Để \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) song song với nhau thì \(\left\{ \begin{array}{l}m - 3 = 2\\4 \ne - 1\end{array} \right. \Leftrightarrow m = 5\).
Vậy với \(m = 5\) thì hai đường thẳng \(\left( {{d_1}} \right)\)và\(\left( {{d_2}} \right)\)song song với nhau.
b) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x - y = 3}\\{3x + 2y = 8}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{2x - y = 3}\\{3x + 2y = 8}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 2x - 3\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)}\\{3x + 2y = 8\,\,\,\,\,\,\,\,\,\left( 2 \right)}\end{array}} \right.\)
Thay (1) vào (2) ta có
\(\begin{array}{l}\left( 2 \right) \Leftrightarrow 3x + 2\left( {2x - 3} \right) = 8\\ \Leftrightarrow 3x + 4x - 6 = 8\\ \Leftrightarrow 7x = 14\\ \Leftrightarrow x = 2.\end{array}\)
Thay \(x = 2\)vào (1) ta được\(y = 2.2 - 3 = 1\).
Vậy hệ phương trình có nghiệm\(\left( {x;y} \right) = \left( {2;1} \right)\).
Câu 3 (VD):
Phương pháp:
Sử dụng định lí Vi – ét.
Nếu phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) có 2 nghiệm \({x_1},{x_2}\) thì
\(\left\{ {\begin{array}{*{20}{l}}{S = {X_1} + {X_2} = \frac{{ - b}}{a}}\\{P = {x_1} \cdot {X_2} = \frac{c}{a}}\end{array}} \right.\)
Cách giải:
Ta có \(\Delta ' = {m^2} - \left( {{m^2} - m - 2} \right) = {m^2} - {m^2} + m + 2 = m + 2\)
Để phương trình có 2 nghiệm phân biệt thì \(\Delta ' > 0 \Leftrightarrow m + 2 > 0 \Leftrightarrow m > - 2\)
Vậy \(m > - 2\) thì phương trình có 2 nghiệm phân biệt \({x_1},{x_2}\)
Áp dụng hệ thức Viet có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}.{x_2} = {m^2} - m - 2\end{array} \right.\)
Để \(\frac{{{x_1}{x_2} + 1}}{{x_1^2 + x_2^2 + 2\left( {1 + {x_1}{x_2}} \right)}} = \frac{1}{6}.\)
\( \Leftrightarrow \frac{{{x_1}{x_2} + 1}}{{x_1^2 + x_2^2 + 2{x_1}{x_1} + 2}} = \frac{1}{6}\)
\( \Leftrightarrow \frac{{{x_1}{x_2} + 1}}{{{{\left( {{x_1} + {x_2}} \right)}^2} + 2}} = \frac{1}{6}\)
\( \Leftrightarrow \frac{{{m^2} - m - 2 + 1}}{{{{\left( {2m} \right)}^2} + 2}} = \frac{1}{6}\)
\( \Leftrightarrow \frac{{{m^2} - m - 1}}{{4{m^2} + 2}} = \frac{1}{6}\)
\( \Leftrightarrow 6{m^2} - 6m - 6 = 4{m^2} + 2\)
\( \Leftrightarrow 2{m^2} - 6m - 8 = 0\)
\( \Leftrightarrow 2\left( {m + 1} \right)\left( {m - 4} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}m = - 1\left( {TM} \right)\\m = 4\left( {TM} \right)\end{array} \right.\)
Vậy m = -1 hoặc m = 4 thỏa mãn bài toán.
Câu 4 (VD):
Phương pháp:
Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Cách giải:
Gọi x là số dãy ghế ban đầu. \(\left( {x > 2,x \in {N^*}} \right)\).
Sau khi cất đi 2 dãy ghế, số dãy ghế còn lại là: \(x - 2\) (dãy).
Số ghế ở mỗi hàng lúc ban đầu là \(\frac{{96}}{x}\) (ghế).
Số ghế ở mỗi hàng sau khi bỏ bớt hai hàng là \(\frac{{110}}{{x - 2}}\) (ghế).
Vì khi cất bớt 2 dãy ghế và mỗi dãy còn lại xếp thêm 1 ghế nên ta có phương trình:
\(\frac{{110}}{{x - 2}} - \frac{{96}}{x} = 1\)
\( \Leftrightarrow \frac{{110x}}{{\left( {x - 2} \right)x}} - \frac{{96\left( {x - 2} \right)}}{{\left( {x - 2} \right)x}} = 1\)
\( \Leftrightarrow \frac{{110x - 96\left( {x - 2} \right)}}{{\left( {x - 2} \right)x}} = 1\)
\( \Leftrightarrow \frac{{110x - 96x + 192}}{{\left( {x - 2} \right)x}} = 1\)
\( \Leftrightarrow \frac{{14x + 192}}{{\left( {x - 2} \right)x}} = 1\)
\( \Leftrightarrow 14x + 192 = {x^2} - 2x\)
\( \Leftrightarrow {x^2} - 16x - 192 = 0\)
\( \Leftrightarrow \left( {x - 24} \right)\left( {x + 8} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 24\left( {tm} \right)\\x = - 8\left( {ktm} \right)\end{array} \right.\)
Vậy số dãy ghế lúc đầu là 24 dãy ghế.
Câu 5 (VD):
Phương pháp:
Áp dụng định lí Pytago và hệ thức lượng trong tam giác cho tam giác ABC vuông tại A đường cao AH ta được: \(A{B^2} = BH.BC\).
Cách giải:
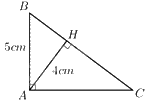
Áp dụng định lý Pytago cho tam giác ABH vuông tại H ta được: \(A{H^2} + B{H^2} = A{B^2}\)
\( \Rightarrow {4^2} + B{H^2} = {5^2}\)
\(\begin{array}{l} \Leftrightarrow 16 + B{H^2} = 25\\ \Leftrightarrow B{H^2} = 9\\ \Leftrightarrow BH = 3\end{array}\)
Áp dụng hệ thức lượng cho tam giác ABC vuông tại A đường cao AH ta được: \(A{B^2} = BH.BC\)
\( \Rightarrow BC = \frac{{A{B^2}}}{{BH}} = \frac{{{5^2}}}{3} = \frac{{25}}{3}\)
Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.4.\frac{{25}}{3} = \frac{{50}}{3}\left( {c{m^2}} \right)\)
Câu 6 (VD):
Cách giải:
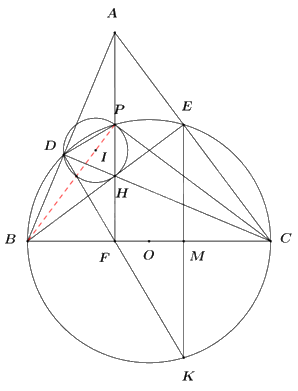
a) Chứng minh ADHE là tứ giác nội tiếp.
Ta có \(\angle BEC = \angle BDC = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \angle ADH = \angle AEH = {90^0}\).
\( \Rightarrow \angle ADH + \angle AEH = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow ADHE\) là tứ giác nội tiếp
(Tứ giác có tổng hai góc đối bằng \({180^0}\)).
b) Đường thẳng AH cắt BC tại F và cắt đường tròn (O) tại điểm P (P nằm giữa A và H). Đường thẳng DF cắt đường tròn (O) tại điểm K (K khác D). Gọi M là giao điểm của EK và BC, I là tâm đường tròn ngoại tiếp tam giác HDP. Chứng minh \(C{E^2} = BC.MC\) và ba điểm B, I, P thẳng hàng.
+) Chứng minh CE2 = BC.MC.
Xét tam giác ABC có: \(\angle BEC = \angle BDC = {90^0}\,\,\left( {cmt} \right) \Rightarrow BE \bot AC,\,\,CD \bot AB\).
Mà \(BE \cap CD = \left\{ H \right\} \Rightarrow H\) là trực tâm của tam giác ABC.
\( \Rightarrow AH \bot BC\) tại F \( \Rightarrow AF \bot BC \Rightarrow \angle BFH = {90^0}\).
Xét tứ giác BFHD có: \(\angle BFH + \angle BDH = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow BFHD\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)).
\( \Rightarrow \angle DFH = \angle DBH = \angle DBE\) (hai góc nội tiếp cùng chắn cung DH)
Mà \(\angle DBE = \angle DKE\) (hai góc nội tiếp cùng chắn cung DE)
\( \Rightarrow \angle DFH = \angle DKE\). Mà 2 góc này ở vị trí hai góc đồng vị bằng nhau.
\( \Rightarrow FP//KE \Rightarrow AF//KE\) (dhnb).
Mà \(AF \bot BC\,\,\left( {cmt} \right) \Rightarrow KE \bot BC\) tại M \( \Rightarrow EM \bot BC\).
Xét tam giác BCE vuông tại E, đường cao EM có: \(C{E^2} = BC.MC\) (hệ thức lượng trong tam giác vuông) (đpcm).
+) Chứng minh ba điểm B, I, P thẳng hàng.
Xét \(\Delta CHF\) và \(\Delta CBD\) có:
$\begin{align} \angle CFH=\angle CDB={{90}^{0}} \\ \angle BCD\,\,chung \\ \Rightarrow \Delta CHF\backsim \Delta CBD\,\,\left( g.g \right) \\ \end{align}$
\( \Rightarrow \frac{{CH}}{{CB}} = \frac{{CF}}{{CD}}\) (cặp cạnh tương ứng tỉ lệ)
\( \Rightarrow CH.CD = CB.CF\) (1)
Ta có: \(\angle CPB = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta CBP\) vuông tại P.
Xét tam giác CBP vuông tại P, đường cao PF có:
\(C{P^2} = CB.CF\) (hệ thức lượng trong tam giác vuông) (2)
Từ (1) và (2) \( \Rightarrow CH.CD = C{P^2} \Rightarrow \frac{{CH}}{{CP}} = \frac{{CP}}{{CD}}\).
Xét \(\Delta CHP\) và \(\Delta CPD\) có:
$\begin{align}\angle PCD\,\,chung \\ \frac{CH}{CP}=\frac{CP}{CD}\,\,\left( cmt \right) \\ \Rightarrow \Delta CHP\backsim \Delta CPD\,\,\left( c.g.c \right) \\ \end{align}$
\( \Rightarrow \angle HPC = \angle PDC = \angle PDH\) (2 góc tương ứng).
Ta có \(\angle HPI = \frac{{{{180}^0} - \angle HIP}}{2} = {90^0} - \frac{{\angle HIP}}{2} = {90^0} - \angle PDH\) (góc ở tâm và góc nội tiếp cùng chắn cung HP)
\( \Rightarrow \angle HIP = {90^0} - \angle HPC \Leftrightarrow \angle HIP + \angle HPC = {90^0} \Leftrightarrow \angle CPI = {90^0}\)
\( \Rightarrow IP \bot PC\) (3)
Mà \(\angle CPB = {90^0}\) (cmt) \( \Rightarrow BP \bot PC\) (4)
Từ (3) và (4) \( \Rightarrow B,\,\,I,\,\,P\) thẳng hàng (đpcm).
Câu 7 (VDC):
Phương pháp:
Áp dụng bất đẳng thức Bu-nhi-a-cốp-xki.
Cách giải:
Áp dụng bất đẳng thức Bu-nhi-a-cốp-xki ta có:
\({\left( {a + b} \right)^2} \le \left( {1 + 1} \right)\left( {{a^2} + {b^2}} \right) = 2\left( {{a^2} + {b^2}} \right)\)
\({\left( {b + c} \right)^2} \le 2\left( {{b^2} + {c^2}} \right)\)
\({\left( {c + a} \right)^2} \le 2\left( {{c^2} + {a^2}} \right)\)
Suy ra: \(P\, \ge \frac{{{a^2}}}{{{a^2} + 4({b^2} + {c^2})}} + \frac{{{b^2}}}{{{b^2} + 4({c^2} + {a^2})}} + \frac{{{c^2}}}{{{c^2} + 4({a^2} + {b^2})}}\)
\(\,\,\, = \frac{{{a^2}}}{{{a^2} + 4({b^2} + {c^2})}} + \frac{1}{3} + \frac{{{b^2}}}{{{b^2} + 4({c^2} + {a^2})}} + \frac{1}{3} + \frac{{{c^2}}}{{{c^2} + 4({a^2} + {b^2})}} + \frac{1}{3} - 1\)
\(\,\,\, = \frac{{4({a^2} + {b^2} + {c^2})}}{{3\left( {{a^2} + 4({b^2} + {c^2})} \right)}} + \frac{{4({a^2} + {b^2} + {c^2})}}{{3\left( {{b^2} + 4({c^2} + {a^2})} \right)}} + \frac{{4({a^2} + {b^2} + {c^2})}}{{3\left( {{c^2} + 4({a^2} + {b^2})} \right)}} - 1\)
\(\,\,\, = \frac{4}{3}({a^2} + {b^2} + {c^2})\left( {\frac{1}{{{a^2} + 4({b^2} + {c^2})}} + \frac{1}{{{b^2} + 4({c^2} + {a^2})}} + \frac{1}{{{c^2} + 4({a^2} + {b^2})}}} \right) - 1\)
Áp dụng bất đẳng thức cộng mẫu số ta được:
\(\frac{1}{{{a^2} + 4({b^2} + {c^2})}} + \frac{1}{{{b^2} + 4({c^2} + {a^2})}} + \frac{1}{{{c^2} + 4({a^2} + {b^2})}} \ge \frac{{{{\left( {1 + 1 + 1} \right)}^2}}}{{9\left( {{a^2} + {b^2} + {c^2}} \right)}} = \frac{1}{{{a^2} + {b^2} + {c^2}}}\)
Do đó: \(P \ge \frac{4}{3}.\left( {{a^2} + {b^2} + {c^2}} \right).\frac{1}{{{a^2} + {b^2} + {c^2}}} - 1 = \frac{4}{3} - 1 = \frac{1}{3}\)
Dấu “=” xảy ra khi và chỉ khi \(a = b = c\)
Vậy giá trị nhỏ nhất của \(P\) là \(\frac{1}{3}\) khi \(a = b = c\).
Câu 1 (VD):
Phương pháp:
a) Căn bậc hai của một số \(a\) là một số \(x\) sao cho \({x^2} = a\)
b) Quy đồng và rút gọn sử dụng hằng đẳng thức.
Cách giải:
a) \(A = \sqrt {48} - 3\sqrt 3 \).
Ta có: \(A = \sqrt {48} - 3\sqrt 3 = \sqrt {{{3.4}^2}} - 3\sqrt 3 = 4\sqrt 3 - 3\sqrt 3 = \sqrt 3 \)
Vậy \(A = \sqrt 3 .\)
b) \(B = \left( {\frac{1}{{\sqrt x + 2}} + \frac{1}{{\sqrt x - 2}}} \right):\frac{{\sqrt x }}{{x - 4}}\) (với \(\left. {x > 0;x \ne 4} \right)\).
Với \(x > 0;x \ne 4\) ta có:
\(\begin{array}{l}B = \left( {\frac{1}{{\sqrt x + 2}} + \frac{1}{{\sqrt x - 2}}} \right):\frac{{\sqrt x }}{{x - 4}}\\\,\,\, = \left( {\frac{{\sqrt x - 2}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}} + \frac{{\sqrt x + 2}}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}} \right).\frac{{x - 4}}{{\sqrt x }}\\\,\,\, = \frac{{2\sqrt x }}{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right)}}.\frac{{x - 4}}{{\sqrt x }}\\\,\,\, = \frac{{2\sqrt x }}{{x - 4}}.\frac{{x - 4}}{{\sqrt x }}\\\,\,\, = 2\end{array}\)
Vậy \(B = 2.\)
Câu 2 (VD):
Phương pháp:
a) Để hai đường thẳng song song thì hệ số góc bằng nhau.
b) Sử dụng phương pháp thế hoặc phương pháp trừ vế.
Cách giải:
Cách giải:
a) Cho hai dường thẳng \(\left( {{d_1}} \right):y = (m - 3)x + 4\left( m \right.\) là tham số) và \(\left( {{d_2}} \right):y = 2x - 1\). Tìm giá trị của \(m\) để hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) song song với nhau.
Để \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) song song với nhau thì \(\left\{ \begin{array}{l}m - 3 = 2\\4 \ne - 1\end{array} \right. \Leftrightarrow m = 5\).
Vậy với \(m = 5\) thì hai đường thẳng \(\left( {{d_1}} \right)\)và\(\left( {{d_2}} \right)\)song song với nhau.
b) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x - y = 3}\\{3x + 2y = 8}\end{array}} \right.\).
\(\left\{ {\begin{array}{*{20}{l}}{2x - y = 3}\\{3x + 2y = 8}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 2x - 3\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)}\\{3x + 2y = 8\,\,\,\,\,\,\,\,\,\left( 2 \right)}\end{array}} \right.\)
Thay (1) vào (2) ta có
\(\begin{array}{l}\left( 2 \right) \Leftrightarrow 3x + 2\left( {2x - 3} \right) = 8\\ \Leftrightarrow 3x + 4x - 6 = 8\\ \Leftrightarrow 7x = 14\\ \Leftrightarrow x = 2.\end{array}\)
Thay \(x = 2\)vào (1) ta được\(y = 2.2 - 3 = 1\).
Vậy hệ phương trình có nghiệm\(\left( {x;y} \right) = \left( {2;1} \right)\).
Câu 3 (VD):
Phương pháp:
Sử dụng định lí Vi – ét.
Nếu phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) có 2 nghiệm \({x_1},{x_2}\) thì
\(\left\{ {\begin{array}{*{20}{l}}{S = {X_1} + {X_2} = \frac{{ - b}}{a}}\\{P = {x_1} \cdot {X_2} = \frac{c}{a}}\end{array}} \right.\)
Cách giải:
Ta có \(\Delta ' = {m^2} - \left( {{m^2} - m - 2} \right) = {m^2} - {m^2} + m + 2 = m + 2\)
Để phương trình có 2 nghiệm phân biệt thì \(\Delta ' > 0 \Leftrightarrow m + 2 > 0 \Leftrightarrow m > - 2\)
Vậy \(m > - 2\) thì phương trình có 2 nghiệm phân biệt \({x_1},{x_2}\)
Áp dụng hệ thức Viet có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}.{x_2} = {m^2} - m - 2\end{array} \right.\)
Để \(\frac{{{x_1}{x_2} + 1}}{{x_1^2 + x_2^2 + 2\left( {1 + {x_1}{x_2}} \right)}} = \frac{1}{6}.\)
\( \Leftrightarrow \frac{{{x_1}{x_2} + 1}}{{x_1^2 + x_2^2 + 2{x_1}{x_1} + 2}} = \frac{1}{6}\)
\( \Leftrightarrow \frac{{{x_1}{x_2} + 1}}{{{{\left( {{x_1} + {x_2}} \right)}^2} + 2}} = \frac{1}{6}\)
\( \Leftrightarrow \frac{{{m^2} - m - 2 + 1}}{{{{\left( {2m} \right)}^2} + 2}} = \frac{1}{6}\)
\( \Leftrightarrow \frac{{{m^2} - m - 1}}{{4{m^2} + 2}} = \frac{1}{6}\)
\( \Leftrightarrow 6{m^2} - 6m - 6 = 4{m^2} + 2\)
\( \Leftrightarrow 2{m^2} - 6m - 8 = 0\)
\( \Leftrightarrow 2\left( {m + 1} \right)\left( {m - 4} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}m = - 1\left( {TM} \right)\\m = 4\left( {TM} \right)\end{array} \right.\)
Vậy m = -1 hoặc m = 4 thỏa mãn bài toán.
Câu 4 (VD):
Phương pháp:
Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Cách giải:
Gọi x là số dãy ghế ban đầu. \(\left( {x > 2,x \in {N^*}} \right)\).
Sau khi cất đi 2 dãy ghế, số dãy ghế còn lại là: \(x - 2\) (dãy).
Số ghế ở mỗi hàng lúc ban đầu là \(\frac{{96}}{x}\) (ghế).
Số ghế ở mỗi hàng sau khi bỏ bớt hai hàng là \(\frac{{110}}{{x - 2}}\) (ghế).
Vì khi cất bớt 2 dãy ghế và mỗi dãy còn lại xếp thêm 1 ghế nên ta có phương trình:
\(\frac{{110}}{{x - 2}} - \frac{{96}}{x} = 1\)
\( \Leftrightarrow \frac{{110x}}{{\left( {x - 2} \right)x}} - \frac{{96\left( {x - 2} \right)}}{{\left( {x - 2} \right)x}} = 1\)
\( \Leftrightarrow \frac{{110x - 96\left( {x - 2} \right)}}{{\left( {x - 2} \right)x}} = 1\)
\( \Leftrightarrow \frac{{110x - 96x + 192}}{{\left( {x - 2} \right)x}} = 1\)
\( \Leftrightarrow \frac{{14x + 192}}{{\left( {x - 2} \right)x}} = 1\)
\( \Leftrightarrow 14x + 192 = {x^2} - 2x\)
\( \Leftrightarrow {x^2} - 16x - 192 = 0\)
\( \Leftrightarrow \left( {x - 24} \right)\left( {x + 8} \right) = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}x = 24\left( {tm} \right)\\x = - 8\left( {ktm} \right)\end{array} \right.\)
Vậy số dãy ghế lúc đầu là 24 dãy ghế.
Câu 5 (VD):
Phương pháp:
Áp dụng định lí Pytago và hệ thức lượng trong tam giác cho tam giác ABC vuông tại A đường cao AH ta được: \(A{B^2} = BH.BC\).
Cách giải:
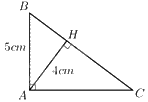
Áp dụng định lý Pytago cho tam giác ABH vuông tại H ta được: \(A{H^2} + B{H^2} = A{B^2}\)
\( \Rightarrow {4^2} + B{H^2} = {5^2}\)
\(\begin{array}{l} \Leftrightarrow 16 + B{H^2} = 25\\ \Leftrightarrow B{H^2} = 9\\ \Leftrightarrow BH = 3\end{array}\)
Áp dụng hệ thức lượng cho tam giác ABC vuông tại A đường cao AH ta được: \(A{B^2} = BH.BC\)
\( \Rightarrow BC = \frac{{A{B^2}}}{{BH}} = \frac{{{5^2}}}{3} = \frac{{25}}{3}\)
Diện tích tam giác ABC là: \({S_{ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.4.\frac{{25}}{3} = \frac{{50}}{3}\left( {c{m^2}} \right)\)
Câu 6 (VD):
Cách giải:
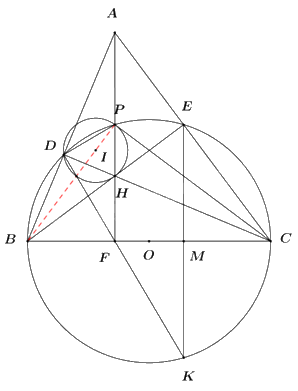
a) Chứng minh ADHE là tứ giác nội tiếp.
Ta có \(\angle BEC = \angle BDC = {90^0}\) (góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow \angle ADH = \angle AEH = {90^0}\).
\( \Rightarrow \angle ADH + \angle AEH = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow ADHE\) là tứ giác nội tiếp
(Tứ giác có tổng hai góc đối bằng \({180^0}\)).
b) Đường thẳng AH cắt BC tại F và cắt đường tròn (O) tại điểm P (P nằm giữa A và H). Đường thẳng DF cắt đường tròn (O) tại điểm K (K khác D). Gọi M là giao điểm của EK và BC, I là tâm đường tròn ngoại tiếp tam giác HDP. Chứng minh \(C{E^2} = BC.MC\) và ba điểm B, I, P thẳng hàng.
+) Chứng minh CE2 = BC.MC.
Xét tam giác ABC có: \(\angle BEC = \angle BDC = {90^0}\,\,\left( {cmt} \right) \Rightarrow BE \bot AC,\,\,CD \bot AB\).
Mà \(BE \cap CD = \left\{ H \right\} \Rightarrow H\) là trực tâm của tam giác ABC.
\( \Rightarrow AH \bot BC\) tại F \( \Rightarrow AF \bot BC \Rightarrow \angle BFH = {90^0}\).
Xét tứ giác BFHD có: \(\angle BFH + \angle BDH = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow BFHD\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)).
\( \Rightarrow \angle DFH = \angle DBH = \angle DBE\) (hai góc nội tiếp cùng chắn cung DH)
Mà \(\angle DBE = \angle DKE\) (hai góc nội tiếp cùng chắn cung DE)
\( \Rightarrow \angle DFH = \angle DKE\). Mà 2 góc này ở vị trí hai góc đồng vị bằng nhau.
\( \Rightarrow FP//KE \Rightarrow AF//KE\) (dhnb).
Mà \(AF \bot BC\,\,\left( {cmt} \right) \Rightarrow KE \bot BC\) tại M \( \Rightarrow EM \bot BC\).
Xét tam giác BCE vuông tại E, đường cao EM có: \(C{E^2} = BC.MC\) (hệ thức lượng trong tam giác vuông) (đpcm).
+) Chứng minh ba điểm B, I, P thẳng hàng.
Xét \(\Delta CHF\) và \(\Delta CBD\) có:
$\begin{align} \angle CFH=\angle CDB={{90}^{0}} \\ \angle BCD\,\,chung \\ \Rightarrow \Delta CHF\backsim \Delta CBD\,\,\left( g.g \right) \\ \end{align}$
\( \Rightarrow \frac{{CH}}{{CB}} = \frac{{CF}}{{CD}}\) (cặp cạnh tương ứng tỉ lệ)
\( \Rightarrow CH.CD = CB.CF\) (1)
Ta có: \(\angle CPB = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta CBP\) vuông tại P.
Xét tam giác CBP vuông tại P, đường cao PF có:
\(C{P^2} = CB.CF\) (hệ thức lượng trong tam giác vuông) (2)
Từ (1) và (2) \( \Rightarrow CH.CD = C{P^2} \Rightarrow \frac{{CH}}{{CP}} = \frac{{CP}}{{CD}}\).
Xét \(\Delta CHP\) và \(\Delta CPD\) có:
$\begin{align}\angle PCD\,\,chung \\ \frac{CH}{CP}=\frac{CP}{CD}\,\,\left( cmt \right) \\ \Rightarrow \Delta CHP\backsim \Delta CPD\,\,\left( c.g.c \right) \\ \end{align}$
\( \Rightarrow \angle HPC = \angle PDC = \angle PDH\) (2 góc tương ứng).
Ta có \(\angle HPI = \frac{{{{180}^0} - \angle HIP}}{2} = {90^0} - \frac{{\angle HIP}}{2} = {90^0} - \angle PDH\) (góc ở tâm và góc nội tiếp cùng chắn cung HP)
\( \Rightarrow \angle HIP = {90^0} - \angle HPC \Leftrightarrow \angle HIP + \angle HPC = {90^0} \Leftrightarrow \angle CPI = {90^0}\)
\( \Rightarrow IP \bot PC\) (3)
Mà \(\angle CPB = {90^0}\) (cmt) \( \Rightarrow BP \bot PC\) (4)
Từ (3) và (4) \( \Rightarrow B,\,\,I,\,\,P\) thẳng hàng (đpcm).
Câu 7 (VDC):
Phương pháp:
Áp dụng bất đẳng thức Bu-nhi-a-cốp-xki.
Cách giải:
Áp dụng bất đẳng thức Bu-nhi-a-cốp-xki ta có:
\({\left( {a + b} \right)^2} \le \left( {1 + 1} \right)\left( {{a^2} + {b^2}} \right) = 2\left( {{a^2} + {b^2}} \right)\)
\({\left( {b + c} \right)^2} \le 2\left( {{b^2} + {c^2}} \right)\)
\({\left( {c + a} \right)^2} \le 2\left( {{c^2} + {a^2}} \right)\)
Suy ra: \(P\, \ge \frac{{{a^2}}}{{{a^2} + 4({b^2} + {c^2})}} + \frac{{{b^2}}}{{{b^2} + 4({c^2} + {a^2})}} + \frac{{{c^2}}}{{{c^2} + 4({a^2} + {b^2})}}\)
\(\,\,\, = \frac{{{a^2}}}{{{a^2} + 4({b^2} + {c^2})}} + \frac{1}{3} + \frac{{{b^2}}}{{{b^2} + 4({c^2} + {a^2})}} + \frac{1}{3} + \frac{{{c^2}}}{{{c^2} + 4({a^2} + {b^2})}} + \frac{1}{3} - 1\)
\(\,\,\, = \frac{{4({a^2} + {b^2} + {c^2})}}{{3\left( {{a^2} + 4({b^2} + {c^2})} \right)}} + \frac{{4({a^2} + {b^2} + {c^2})}}{{3\left( {{b^2} + 4({c^2} + {a^2})} \right)}} + \frac{{4({a^2} + {b^2} + {c^2})}}{{3\left( {{c^2} + 4({a^2} + {b^2})} \right)}} - 1\)
\(\,\,\, = \frac{4}{3}({a^2} + {b^2} + {c^2})\left( {\frac{1}{{{a^2} + 4({b^2} + {c^2})}} + \frac{1}{{{b^2} + 4({c^2} + {a^2})}} + \frac{1}{{{c^2} + 4({a^2} + {b^2})}}} \right) - 1\)
Áp dụng bất đẳng thức cộng mẫu số ta được:
\(\frac{1}{{{a^2} + 4({b^2} + {c^2})}} + \frac{1}{{{b^2} + 4({c^2} + {a^2})}} + \frac{1}{{{c^2} + 4({a^2} + {b^2})}} \ge \frac{{{{\left( {1 + 1 + 1} \right)}^2}}}{{9\left( {{a^2} + {b^2} + {c^2}} \right)}} = \frac{1}{{{a^2} + {b^2} + {c^2}}}\)
Do đó: \(P \ge \frac{4}{3}.\left( {{a^2} + {b^2} + {c^2}} \right).\frac{1}{{{a^2} + {b^2} + {c^2}}} - 1 = \frac{4}{3} - 1 = \frac{1}{3}\)
Dấu “=” xảy ra khi và chỉ khi \(a = b = c\)
Vậy giá trị nhỏ nhất của \(P\) là \(\frac{1}{3}\) khi \(a = b = c\).
Kỳ thi tuyển sinh vào lớp 10 tại Hà Tĩnh luôn là một cột mốc quan trọng trong quá trình học tập của học sinh THCS. Môn Toán, với vai trò then chốt, đòi hỏi học sinh phải có sự chuẩn bị kỹ lưỡng về kiến thức và kỹ năng. Đề thi vào 10 môn Toán Hà Tĩnh năm 2023 tiếp tục duy trì cấu trúc đề thi truyền thống, tập trung vào các chủ đề chính như Đại số, Hình học và một số kiến thức tích hợp. Tuy nhiên, đề thi cũng có những điểm mới, đòi hỏi học sinh phải có khả năng vận dụng kiến thức linh hoạt và sáng tạo.
Thông thường, đề thi vào 10 môn Toán Hà Tĩnh năm 2023 có thời gian làm bài khoảng 120 phút. Đề thi thường bao gồm các dạng câu hỏi sau:
Để đạt kết quả tốt trong kỳ thi vào 10 môn Toán Hà Tĩnh năm 2023, học sinh cần nắm vững các chủ đề kiến thức sau:
Để luyện thi vào 10 môn Toán Hà Tĩnh năm 2023 hiệu quả, học sinh cần có một kế hoạch học tập khoa học và hợp lý. Dưới đây là một số gợi ý:
Ngoài bộ đề thi do giaitoan.edu.vn cung cấp, học sinh có thể tham khảo thêm các tài liệu ôn thi sau:
Trước khi bước vào phòng thi, hãy đảm bảo bạn đã chuẩn bị đầy đủ các dụng cụ cần thiết như bút, thước, máy tính bỏ túi. Trong quá trình làm bài, hãy đọc kỹ đề bài, phân tích đề bài và lập kế hoạch giải bài một cách hợp lý. Hãy tự tin vào khả năng của mình và cố gắng hết sức để đạt kết quả tốt nhất.
Giaitoan.edu.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục tri thức. Chúng tôi hy vọng bộ đề thi vào 10 môn Toán Hà Tĩnh năm 2023 này sẽ là một công cụ hữu ích giúp các em đạt được kết quả tốt nhất trong kỳ thi sắp tới. Chúc các em thành công!