Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp các đề thi thử vào lớp 10 môn Toán chất lượng cao. Đề số 35 là một trong những đề thi được thiết kế để giúp học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin bước vào kỳ thi quan trọng.
Đề thi này bao gồm các dạng bài tập đa dạng, từ trắc nghiệm đến tự luận, bao phủ đầy đủ các kiến thức trọng tâm của chương trình Toán lớp 9.
Đề thi vào lớp 10 môn Toán - Đề số 35 có đáp án và lời giải chi tiết
Đề bài
Bài 1 (1 điểm): Các đẳng thức sau đúng hay sai, giải thích?
a) \(\sqrt {{{\left( { - 3} \right)}^2}} = - 3.\)
b) \(\dfrac{{x - y}}{{\sqrt x + \sqrt y }} = \sqrt x - \sqrt y \) với \(x > 0,\;\;y > 0.\)
Bài 2 (2,0 điểm): Giải phương trình và hệ phương trình sau:
\(a)\;\;2{x^2} - 5x + 2 = 0.\)
\(b)\;\left\{ \begin{array}{l}2x + y = 1\\3x - 2y = 5\end{array} \right..\)
Bài 3 (1,5 điểm):
Cho hai hàm số \(\left( P \right):\;\;y = {x^2}\) và \(d:\;\;y = x + 2m + 10,\) với \(m\) là tham số.
a) Vẽ đồ thị \(\left( P \right)\) trên hệ trục tọa độ \(Oxy.\)
b) Tìm giá trị của tham số \(m\) biết \(d\) cắt \(\left( P \right)\) tại điểm có hoành độ bằng \(5.\)
Bài 4 (2,0 điểm):
Đua ghe ngo là một trong những nét văn hóa truyền thống độc đáo của đồng bào dân tộc Khmer Nam Bộ. Cuộc đua luôn thu hút hàng trăm ngàn người tham dự vào dịp lễ hội Ok-om-bok hàng năm (rằm tháng 10 âm lịch). Đua ghe ngo là dịp để các đội ghe đến tham gia tranh tài, qua đó nhằm tôn vinh, nâng cao ý thức bảo tồn di sản văn hóa truyền thống của địa phương, thể hiện tinh thần đoàn kết dân tộc, khơi dậy niềm tự hào, tinh thần yêu quê hương đất nước

Tại lễ hội đua ghe ngo Sóc Trăng, có 56 đội ghe trong và ngoài đăng ký tham gia. Lúc đầu ban tổ chức dự kiến chia 56 đội thành các bảng đấu với số đội ở mỗi bảng bằng nhau. Tuy nhiên, đến ngày bốc thăm chia bảng thì có 1 đội không tham dự được, vì vậy ban tổ chức quyết định tăng ở mỗi bảng thêm 1 đội, do đó tổng số bảng đấu giảm đi 3 bảng. Hỏi số bảng đấu dự kiến lúc đầu là bao nhiêu?
Bài 5 (3,5 điểm): Cho tam giác \(ABC\) có ba góc nhọn, nội tiếp đường tròn \(\left( O \right),\;\;AB > AC\) và các đường cao \(AD,\;\;BE,\;\;CF\) cắt nhau tại \(H.\)
a) Gọi \(I\) là trung điểm của \(AH,\) chứng minh \(AEHF\) nội tiếp đường tròn \(\left( I \right).\)
b) Chứng minh \(DB.DC = DA.DH.\)
c) Gọi \(K\) là giao điểm khác \(A\) của hai đường tròn \(\left( O \right)\) và \(\left( I \right).\) Chứng minh \(OI//HK.\)
Lời giải chi tiết
Bài 1:
Các đẳng thức sau đúng hay sai, giải thích?
a) \(\sqrt {{{\left( { - 3} \right)}^2}} = - 3.\)
b) \(\dfrac{{x - y}}{{\sqrt x + \sqrt y }} = \sqrt x - \sqrt y \) với \(x > 0,\;\;y > 0.\)
a) Ta có: \(\sqrt {{{\left( { - 3} \right)}^2}} = \left| { - 3} \right| = 3 \Rightarrow \) biểu thức \(\sqrt {{{\left( { - 3} \right)}^2}} = - 3\) sai.
b) \(\dfrac{{x - y}}{{\sqrt x + \sqrt y }} = \dfrac{{\left( {\sqrt x - \sqrt y } \right)\left( {\sqrt x + \sqrt y } \right)}}{{\sqrt x + \sqrt y }} \)\(\,= \sqrt x - \sqrt y .\,\,\left( {x > 0;y > 0} \right)\)
\( \Rightarrow \) Biểu thức \(\dfrac{{x - y}}{{\sqrt x + \sqrt y }} = \sqrt x - \sqrt y \) đúng.
Bài 2:
Giải phương trình và hệ phương trình sau:
\(a)\;\;2{x^2} - 5x + 2 = 0.\)
Ta có: \(\Delta = {b^2} - 4ac = {\left( { - 5} \right)^2} - 4.2.2 = 9 > 0\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = \dfrac{{5 + \sqrt 9 }}{{2.2}} = 2\\{x_2} = \dfrac{{5 - \sqrt 9 }}{{2.2}} = \dfrac{1}{2}\end{array} \right..\)
Vậy phương trình có tập nghiệm: \(S = \left\{ {\dfrac{1}{2};\;\;2} \right\}.\)
\(b)\;\;\left\{ \begin{array}{l}2x + y = 1\\3x - 2y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x + 2y = 2\\3x - 2y = 5\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}7x = 7\\y = 1 - 2x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 1\end{array} \right..\)
Vậy hệ phương trình có nghiệm duy nhất: \(\left( {x;\;y} \right) = \left( {1; - 1} \right).\)
Bài 3:
Cho hai hàm số \(\left( P \right):\;\;y = {x^2}\) và \(d:\;\;y = x + 2m + 10,\) với \(m\) là tham số.
a) Vẽ đồ thị \(\left( P \right)\) trên hệ trục tọa độ \(Oxy.\)
Ta có bảng giá trị:
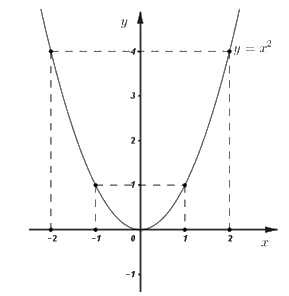
\(x\) | \( - 2\) | \( - 1\) | \(0\) | \(1\) | \(2\) |
\(y = {x^2}\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |
Đồ thị hàm số \(\left( P \right):\;\;y = {x^2}\) là paraol đi qua các điểm \(\left( { - 2;\;4} \right),\;\left( { - 1;\;1} \right),\;\left( {0;\;0} \right),\;\left( {1;\;1} \right),\;\left( {2;\;4} \right).\)
b) Tìm giá trị của tham số \(m\) biết \(d\) cắt \(\left( P \right)\) tại điểm có hoành độ bằng \(5.\)
Phương trình hoành độ giao điểm của \(d\) và \(\left( P \right)\) là: \({x^2} = x + 2m + 10 \Leftrightarrow {x^2} - x - 2m - 10 = 0.\;\;\left( * \right)\)
\(d\) cắt \(\left( P \right) \Leftrightarrow \left( * \right)\) có nghiệm \( \Leftrightarrow \Delta \ge 0 \Leftrightarrow 1 + 4\left( {2m + 10} \right) \ge 0 \Leftrightarrow m \ge - \dfrac{{41}}{8}.\)
\(d\) cắt \(\left( P \right)\) tại điểm có hoành độ bằng \(5 \Rightarrow x = 5\) là nghiệm của phương trình (*).
\( \Rightarrow \left( * \right) \Leftrightarrow {5^2} - 5 - 2m - 10 = 0\)
\(\Leftrightarrow 2m = 10 \Leftrightarrow m = 5.\;\;\left( {tm} \right)\)
Vậy \(m = 5\) thỏa mãn yêu cầu bài toán.
Bài 4:
Tại lễ hội đua ghe ngo Sóc Trăng, có 56 đội ghe trong và ngoài đăng ký tham gia. Lúc đầu ban tổ chức dự kiến chia 56 đội thành các bảng đấu với số đội ở mỗi bảng bằng nhau. Tuy nhiên, đến ngày bốc thăm chia bảng thì có 1 đội không tham dự được, vì vậy ban tổ chức quyết định tăng ở mỗi bảng thêm 1 đội, do đó tổng số bảng đấu giảm đi 3 bảng. Hỏi số bảng đấu dự kiến lúc đầu là bao nhiêu?
Gọi số đội trong mỗi bảng ban đầu là \(x\) (đội), \(\left( {0 < x < 56,\;\;x \in N} \right).\)
Gọi số bảng được chia ban đầu là \(y\) (bảng), \(\left( {3 < y < 56,\;\;y \in N} \right).\)
Khi đó ta có phương trình:\(xy = 56\;\;\;\left( 1 \right)\)
Có 1 đội không tham dự được nên có \(56 - 1 = 55\) đội tham dự được.
Mỗi bảng thêm 1 đội nên số đội trong mỗi bảng lúc này là: \(x + 1\) (đội).
Tổng số bảng đấu giảm đi 3 nên số bảng đấu lúc này là: \(y - 3\) (bảng).
Theo đề bài ta có phương trình:
\(\left( {x + 1} \right)\left( {y - 3} \right) = 55\\ \Leftrightarrow y - 3x - 3 + xy = 55 \\\Leftrightarrow y - 3x = 58 - xy\\ \Leftrightarrow y - 3x = 2\;\;\;\;\left( 2 \right).\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) ta có hệ phương trình:
\(\left\{ \begin{array}{l}xy = 56\\y - 3x = 2\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}y = 2 + 3x\\x\left( {2 + 3x} \right) = 56\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}y = 3x + 2\\3{x^2} + 2x - 56 = 0\end{array} \right.\)
\(\Leftrightarrow \left\{ \begin{array}{l}y = 3x + 2\\\left( {x - 4} \right)\left( {3x + 14} \right) = 0\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}y = 3x + 2\\\left[ \begin{array}{l}x = 4\;\;\left( {tm} \right)\\x = - \dfrac{{14}}{3}\;\;\;\left( {ktm} \right)\end{array} \right.\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 14\;\;\left( {tm} \right)\end{array} \right..\)
Vậy số bảng đấu dự kiến lúc đầu là 14 bảng đấu.
Bài 5:
Cho tam giác \(ABC\) có ba góc nhọn, nội tiếp đường tròn \(\left( O \right),\;\;AB > AC\) và các đường cao \(AD,\;\;BE,\;\;CF\) cắt nhau tại \(H.\)
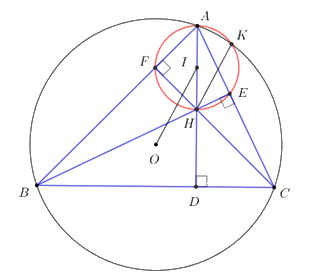
a) Gọi \(I\) là trung điểm của \(AH,\) chứng minh \(AEHF\) nội tiếp đường tròn \(\left( I \right).\)
Xét tứ giác \(AEHF\) ta có: \(\angle AFH = \angle AEH = {90^0}\) (gt) \( \Rightarrow \angle AFH + \angle AEH = {180^0}\).
\( \Rightarrow AEHF\) nội tiếp đường tròn đường kính AH (Tứ giác có tổng hai góc đối bằng 1800).
\(\angle AFH,\;\angle AEH = {90^0} \Rightarrow \angle AFH,\;\angle AEH\) cùng nhìn đoạn \(AH\) dưới góc \({90^0}.\)
Mà I là trung điểm của AH.
Vậy tứ giác AEHF nội tiếp đường tròn \(\left( I \right)\) đườn kính AH.
b) Chứng minh \(DB.DC = DA.DH.\)
Ta có: \(\angle AHF + \angle FAH = {90^0}\) (\(\Delta AFH\) vuông tại \(F\)).
\(\angle ABD + \angle DAB = {90^0}\) (\(\Delta ABD\) vuông tại \(D\)).
\( \Rightarrow \angle AHF = \angle ABD\) (cùng phụ với \(\angle FAH\))
Mà \(\angle DHC = \angle AHF\) (hai góc đối đỉnh).
\( \Rightarrow \angle ABD = \angle DHC\;\;\left( { = \angle AHF} \right).\)
Xét \(\Delta ABD\) và \(\Delta CHD\) ta có:
\(\begin{array}{l}\angle ADB = \angle HDC = {90^0}\\\angle ABD = \angle DHC\;\;\left( {cmt} \right)\\ \Rightarrow \Delta ABD \sim \Delta CHD\;\;\left( {g - g} \right)\\ \Rightarrow \dfrac{{DB}}{{DH}} = \dfrac{{DA}}{{DC}} \Leftrightarrow DB.DC = DA.DH.\;\;\left( {dpcm} \right).\end{array}\)
c) Gọi \(K\) là giao điểm khác \(A\) của hai đường tròn \(\left( O \right)\) và \(\left( I \right).\) Chứng minh \(OI//HK.\)
Ta có:
\(A;K \in \left( I \right) \Rightarrow IA = IK \Rightarrow I\) thuộc trung trực của AK;
\(A;K \in \left( O \right) \Rightarrow OA = OK \Rightarrow O\) thuộc trung trực của AK;
\( \Rightarrow OI\) là trung trực của AK \( \Rightarrow OI \bot AK\).
Lại có \(\angle AKH\) là góc nội tiếp chắn nửa đường tròn \(\left( I \right) \Rightarrow \angle AKH = {90^0} \Rightarrow HK \bot AK\).
\( \Rightarrow OI//HK\) (cùng vuông góc với AK) (đpcm).
Đề thi vào lớp 10 môn Toán là một kỳ thi quan trọng đánh giá năng lực học tập của học sinh sau nhiều năm học tập. Để đạt kết quả tốt, việc luyện tập thường xuyên với các đề thi thử là vô cùng cần thiết. Đề số 35 mà giaitoan.edu.vn cung cấp được xây dựng dựa trên cấu trúc đề thi chính thức, giúp học sinh làm quen với áp lực thời gian và các dạng bài tập thường gặp.
Đề thi Đề số 35 bao gồm các phần chính sau:
Câu 1 (Trắc nghiệm): Câu hỏi về phép biến đổi biểu thức đại số. Yêu cầu học sinh phải nắm vững các quy tắc biến đổi và tính toán chính xác.
Câu 2 (Trắc nghiệm): Câu hỏi về hình học, liên quan đến các tính chất của tam giác, đường tròn hoặc các hình khối không gian.
Câu 3 (Trắc nghiệm): Câu hỏi về số học, tập trung vào các khái niệm như ước số, bội số, phân số và các phép toán trên số.
Câu 4 (Trắc nghiệm): Câu hỏi về các khái niệm toán học thường dùng, như hàm số, phương trình, bất phương trình.
Câu 5 (Trắc nghiệm): Câu hỏi tổng hợp, đòi hỏi học sinh phải kết hợp kiến thức từ nhiều lĩnh vực khác nhau để giải quyết.
Câu 1 (Tự luận): Bài toán về giải phương trình bậc hai. Yêu cầu học sinh phải sử dụng các công thức và phương pháp giải phương trình đã học.
Câu 2 (Tự luận): Bài toán về chứng minh đẳng thức hình học. Yêu cầu học sinh phải nắm vững các định lý và tính chất hình học để chứng minh.
Câu 3 (Tự luận): Bài toán về giải bài toán thực tế ứng dụng kiến thức toán học. Yêu cầu học sinh phải phân tích đề bài, xây dựng mô hình toán học và giải quyết.
Câu 4 (Tự luận): Bài toán về tìm giá trị lớn nhất hoặc nhỏ nhất của một biểu thức. Yêu cầu học sinh phải sử dụng các phương pháp tối ưu hóa để giải quyết.
Câu 5 (Tự luận): Bài toán tổng hợp, đòi hỏi học sinh phải vận dụng kiến thức từ nhiều lĩnh vực khác nhau để giải quyết.
giaitoan.edu.vn cung cấp đáp án chi tiết và hướng dẫn giải cho từng câu hỏi trong đề thi Đề số 35. Học sinh có thể tham khảo để tự kiểm tra kết quả và hiểu rõ hơn về cách giải các bài toán.
giaitoan.edu.vn hy vọng rằng đề thi Đề số 35 sẽ là một công cụ hữu ích giúp các em học sinh ôn tập và chuẩn bị tốt nhất cho kỳ thi vào lớp 10 môn Toán. Chúc các em thành công!