Giaitoan.edu.vn xin giới thiệu bộ đề thi tuyển sinh vào lớp 10 môn Toán tỉnh Bình Phước năm 2019 chính thức. Đây là tài liệu vô cùng hữu ích cho các em học sinh đang chuẩn bị cho kỳ thi quan trọng này.
Đề thi được biên soạn theo cấu trúc đề thi chính thức, giúp các em làm quen với dạng đề và rèn luyện kỹ năng giải toán. Bên cạnh đó, chúng tôi còn cung cấp đáp án chi tiết và lời giải bài tập để các em có thể tự học và kiểm tra kiến thức.
Câu 1 (2 điểm): 1) Tính giá trị các biểu thức sau:
Câu 1 (2 điểm):
1) Tính giá trị các biểu thức sau: \(A = 3\sqrt {49} - \sqrt {25} \)
2) Cho biểu thức: \(P = \left( {\dfrac{{\sqrt x }}{{\sqrt {x - 1} }} + \dfrac{{\sqrt x }}{{x - \sqrt x }}} \right):\dfrac{{\sqrt x + 1}}{3}\) với \(x > 0;\,\,x \ne 1\)
a) Rút gọn biểu thức \(P.\) b) Tìm giá trị của \(x\) để \(P = 1\)
Câu 2 (2,0 điểm):
1) Cho parabol \(\left( P \right)\) và đường thẳng \(\left( d \right):\,y = x + 2\)
a) Vẽ parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng một hệ trục tọa độ \(Oxy\)
b) Viết phương trình đường thẳng \(\left( {{d_1}} \right):\,y = ax + b\) song song với \(\left( d \right)\) và cắt \(\left( P \right)\) tại điểm \(A\) có hoành độ bằng \( - 2\) .
2) Không sử dụng máy tính, giải hệ phương trình: \(\left\{ \begin{array}{l}2x + y = 5\\x + 2y = 4\end{array} \right.\)
Câu 3 (2,5 điểm):
1) Cho phương trình: \({x^2} - \left( {m + 2} \right)x + m + 8 = 0\,\,\,\,\left( 1 \right)\) Với \(m\) là tham số.
a) Giải phương trình \(\left( 1 \right)\) khi \(m = - 8\)
b) Tìm các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm dương phân biệt \({x_1},\,{x_2}\) thỏa mãn hệ thức: \(x_1^3 - {x_2} = 0.\)
2) Nông trường cao su Minh Hưng phải khai thác 260 tấn mủ trong một thời gian nhất định. Trên thực tế, mỗi ngày nông trường đề khai thác vượt định mức 3 tấn. Do đó, nông trường đã khai thác được 26 tấn và xong trước thời hạn 1 ngày. Hỏi theo kế hoạch mỗi ngày nông trường khai thác được bao nhiêu tấn mủ cao su.
Câu 4 (1,0 điểm):
Cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\)và đường trung tuyến \(AM\). Biết \(AH = 3cm;\,HB = 4cm.\) Hãy tính \(AB,AC,AM\) và diện tích tam giác \(ABC.\)
Câu 5 (2,5 điểm):
Cho đường tròn tâm \(O\) đường kính \(AB = 2R.\) Gọi \(C\) là trung điểm của \(OA,\) qua \(C\) kẻ đường thẳng vuông góc với \(OA\) cắt đường tròn \(\left( O \right)\) tại hai điểm phân biệt \(M\) và \(N\) . Trên cung nhỏ \(BM\) lấy điểm \(K\) (\(K\) khác \(B\) và \(M\)). Gọi \(H\) là giao điểm của \(AK\) và \(MN.\)
a) Chứng minh tứ giác \(BCHK\) nội tiếp đường tròn.
b) Chứng minh \(AK.AH = {R^2}.\)
c) Trên tia \(KN\) lấy điểm \(I\) sao cho \(KI = KM.\) Chứng minh \(NI = BK.\)
Câu 1:
Phương pháp:
1) Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,A < 0\end{array} \right..\)
2) a) Quy đồng, rút gọn biểu thức.
b) Nhân chéo, giải tìm \(x\).
Cách giải:
1) Tính giá trị các biểu thức sau:
\(\begin{array}{l}A = 3\sqrt {49} - \sqrt {25} = 3\sqrt {{7^2}} - \sqrt {{5^2}} = 3.7 - 5 = 21 - 5 = 16\\B = \sqrt {{{\left( {3 - 2\sqrt 5 } \right)}^2}} - \sqrt {20} = \left| {3 - 2\sqrt 5 } \right| - \sqrt {{2^2}.5} = 2\sqrt 5 - 3 - 2\sqrt 5 = - 3\end{array}\)
2) Cho biểu thức \(P = \left( {\dfrac{{\sqrt x }}{{\sqrt x - 1}} + \dfrac{{\sqrt x }}{{x - \sqrt x }}} \right):\dfrac{{\sqrt x + 1}}{3}\) với \(x > 0,\,\,x \ne 1\).
a) Rút gọn biểu thức \(P\).
\(\begin{array}{l}P = \left( {\dfrac{{\sqrt x }}{{\sqrt x - 1}} + \dfrac{{\sqrt x }}{{x - \sqrt x }}} \right):\dfrac{{\sqrt x + 1}}{3} = \left( {\dfrac{{\sqrt x }}{{\sqrt x - 1}} + \dfrac{{\sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}}} \right):\dfrac{{\sqrt x + 1}}{3}\\\,\,\,\, = \dfrac{{x + \sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}}.\dfrac{3}{{\sqrt x + 1}} = \dfrac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\sqrt x \left( {\sqrt x - 1} \right)}}.\dfrac{3}{{\sqrt x + 1}}\\\,\,\,\, = \dfrac{3}{{\sqrt x - 1}}.\end{array}\)
Vậy \(P = \dfrac{3}{{\sqrt x - 1}}\).
b) Tìm giá trị của \(x\) để \(P = 1\).
\(P = 1 \Leftrightarrow \dfrac{3}{{\sqrt x - 1}} = 1 \Leftrightarrow \sqrt x - 1 = 3 \Leftrightarrow \sqrt x = 4 \Leftrightarrow x = 16\,\,\left( {tm} \right)\).
Vậy để \(P = 1\) thì \(x = 16\).
Câu 2:
Phương pháp:
Phương pháp:
1) a) Lập bảng giá trị, xác định các điểm đồ thị hàm số \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\) đi qua và vẽ đồ thị hàm số.
b) Đường thẳng \({d_1}:\,\,y = {a_1}x + {b_1}\) và \({d_2}:\,\,y = {a_2}x + {b_2}\) là hai đường thẳng song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\)
Tìm tọa độ giao điểm A của hai đồ thị hàm số \(\left( {{d_1}} \right)\) và \(\left( P \right)\) rồi thay vào phương trình \(\left( {{d_1}} \right)\) tìm \(b.\)
2) Giải hệ phương trình bằng phương pháp thế hoặc phương pháp cộng đại số.
Cách giải:
1) a) Vẽ parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng một hệ trục tọa độ \(Oxy.\)
Ta có bảng giá trị:
+) Vẽ đồ thị hàm số \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\)
\(x\) | \( - 4\) | \( - 2\) | \(0\) | \(2\) | \(4\) |
\(y = \dfrac{1}{2}{x^2}\) | \(8\) | \(2\) | \(0\) | \(2\) | \(8\) |
Vậy đồ thị hàm số\(\left( P \right):\,\,\,y = \dfrac{1}{2}{x^2}\) là đường cong đi qua các điểm \(\left( { - 4;\,\,8} \right),\,\,\,\left( { - 2;\,\,2} \right),\,\,\,\left( {0;\,\,0} \right),\,\,\,\left( {2;\,\,2} \right),\,\,\,\left( {4;\,\,8} \right).\)
+) Vẽ đồ thị hàm số \(\left( d \right):\,\,\,y = x + 2:\)
\(x\) | \(0\) | \( - 2\) |
\(y = x + 2\) | \(2\) | \(0\) |
Đồ thị hàm số \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\) và \(\left( d \right):\,\,\,y = x + 2:\)
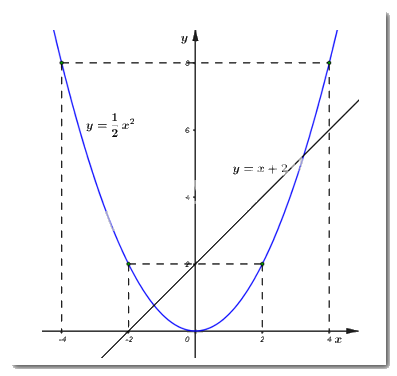
b) Viết phương trình đường thẳng \(\left( {{d_1}} \right):\,\,y = ax + b\) song song với \(\left( d \right)\) và cắt \(\left( P \right)\) tại điểm \(A\) có hoành độ bằng \( - 2.\)
Ta có đường thẳng \(\left( {{d_1}} \right):\,\,y = ax + b\) song song với đường thẳng \(\left( d \right):\,\,\,y = x + 2 \Rightarrow \left\{ \begin{array}{l}a = 1\\b \ne 2\end{array} \right..\)
\( \Rightarrow \left( {{d_1}} \right):\,\,\,y = x + b.\)
Gọi \(A\left( { - 2;\,\,{y_A}} \right)\) là giao điểm của đường thẳng \(\left( {{d_1}} \right)\) và đồ thị \(\left( P \right) \Rightarrow A \in \left( P \right)\)
\( \Rightarrow {y_A} = \dfrac{1}{2}.{\left( { - 2} \right)^2} = 2 \Rightarrow A\left( { - 2;\,\,2} \right).\)
Lại có \(A \in \left( {{d_1}} \right)\) nên thay \(x = - 2;y = 2\) vào phương trình đường thẳng \(\left( {{d_1}} \right):\,\,\,y = x + b\) ta được
\(2 = - 2 + b \Leftrightarrow b = 4\,\,\left( {tm} \right)\)
Vậy đường thẳng \(\left( {{d_1}} \right)\) có phương trình: \(y = x + 4.\)
2) Không sử dụng máy tính, giải hệ phương trình: \(\left\{ \begin{array}{l}2x + y = 5\\x + 2y = 4\end{array} \right..\)
\(\begin{array}{l}\left\{ \begin{array}{l}2x + y = 5\\x + 2y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 5 - 2x\\x + 2\left( {5 - 2x} \right) = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 5 - 2x\\x + 10 - 4x = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 5 - 2x\\3x = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 5 - 2.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right..\end{array}\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;\,\,y} \right) = \left( {2;\,\,1} \right).\)
Câu 3:
Phương pháp:
1) a) Thay \(m\) và phương trình và giải phương trình bậc hai ẩn \(x\).
b) + Phương trình \(\left( 1 \right)\) có hai nghiệm dương phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta > 0\\S > 0\\P > 0\end{array} \right.\)
+ Rút \({x_2} = x_1^2\) thay vào điều kiện \({x_1}{x_2} = \dfrac{c}{a}\) tìm nghiệm \({x_1},{x_2}\).
+ Thay \({x_1},{x_2}\) tìm được ở trên vào \({x_1} + {x_2} = - \dfrac{b}{a}\) tìm \(m\).
2) Giải bài toán bằng cách lập phương trình
Bước 1: Chọn ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết. Lập phương trình
Bước 3: Giải phương trình rồi so sánh với điều kiện để chọn ra các giá trị thích hợp và kết luận.
Cách giải:
1) a) Thay \(m = - 8\) vào phương trình \(\left( 1 \right)\) ta được:
\({x^2} - \left( { - 8 + 2} \right)x + \left( { - 8} \right) + 8 = 0 \Leftrightarrow {x^2} + 6x = 0 \Leftrightarrow x\left( {x + 6} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 6\end{array} \right.\).
Vậy với \(m = - 8\) thì phương trình có tập nghiệm \(S = \left\{ {0; - 6} \right\}.\)
b) Phương trình \(\left( 1 \right)\) có hai nghiệm dương phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}a = 1 \ne 0\\\Delta > 0\\S > 0\\P > 0\end{array} \right.\)
Có \(\Delta {\rm{ = }}{\left( {m + 2} \right)^2} - 4\left( {m + 8} \right) = {m^2} + 4m + 4 - 4m - 32 > 0 \Leftrightarrow {m^2} - 28 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 2\sqrt 7 \\m < - 2\sqrt 7 \end{array} \right.\,\,\,\,\,\,\left( 1 \right)\).
\(S = - \dfrac{b}{a} = m + 2 > 0 \Leftrightarrow m > - 2\,\,\,\,\,\,\left( 2 \right)\).
\(P = \dfrac{c}{a} = m + 8 > 0 \Leftrightarrow m > - 8\,\,\,\,\,\left( 3 \right)\).
Kết hợp các điều kiện (1), (2), (3) ta được \(\left[ \begin{array}{l}m > 2\sqrt 7 \\ - 8 < m < 2\sqrt 7 \end{array} \right..\)
Theo bài ra ta có:
\(\begin{array}{l}x_1^3 - {x_2} = 0 \Leftrightarrow x_1^3 = {x_2} \Leftrightarrow {x_1}{x_2} = x_1^4 = m + 8 \Leftrightarrow {x_1} = \sqrt[4]{{m + 8}} \Rightarrow {x_2} = \sqrt[4]{{{{\left( {m + 8} \right)}^3}}}\\ \Rightarrow {x_1} + {x_2} = m + 2 \Leftrightarrow \sqrt[4]{{m + 8}} + \sqrt[4]{{{{\left( {m + 8} \right)}^3}}} = m + 8 - 6\end{array}\)
Đặt \(\sqrt[4]{{m + 8}} = t\,\,\left( {t \ge 0} \right)\), ta có
\(\begin{array}{l}\,\,\,\,\,\,\,t + {t^3} = {t^4} - 6\\ \Leftrightarrow {t^4} - {t^3} - t - 6 = 0\\ \Leftrightarrow {t^4} - 16 - \left( {{t^3} + t - 10} \right) = 0\\ \Leftrightarrow \left( {{t^2} - 4} \right)\left( {{t^2} + 4} \right) - \left( {{t^3} - 8 + t - 2} \right) = 0\\ \Leftrightarrow \left( {t - 2} \right)\left( {t + 2} \right)\left( {{t^2} + 4} \right) - \left[ {\left( {t - 2} \right)\left( {{t^2} + 2t + 4} \right) + \left( {t - 2} \right)} \right] = 0\\ \Leftrightarrow \left( {t - 2} \right)\left( {t + 2} \right)\left( {{t^2} + 4} \right) - \left( {t - 2} \right)\left( {{t^2} + 2t + 5} \right) = 0\\ \Leftrightarrow \left( {t - 2} \right)\left( {{t^3} + 2{t^2} + 4t + 8 - {t^2} - 2t - 5} \right) = 0\\ \Leftrightarrow \left( {t - 2} \right)\left( {{t^3} + {t^2} + 2t + 3} \right) = 0\\ \Leftrightarrow t = 2\,\,\left( {Do\,\,\,t \ge 0 \Rightarrow {t^3} + {t^2} + 2t + 3 > 0} \right)\end{array}\)
\( \Rightarrow \sqrt[4]{{m + 8}} = 2 \Leftrightarrow m + 8 = {2^4} = 16 \Leftrightarrow m = 8\,\,\left( {tm} \right)\).
Vậy \(m = 8\).
2) Gọi số tấn mủ cao su mỗi ngày nông trường khai thác được là \(x\) tấn \(\left( {0 < x < 260} \right)\)
\( \Rightarrow \) Thời gian theo dự định khai thác mủ cao su của nông trường là \(\dfrac{{260}}{x}\) (ngày)
Theo thực tế mỗi ngày nông trường khai thác được số tấn mủ cao su là: \(x + 3\) (tấn)
\( \Rightarrow \) Thời gian theo thực tế khai thác mủ cao su của nông trường là \(\dfrac{{261}}{{x + 3}}\) (ngày)
Vì nông trường khai thác xong trước thời hạn 1 ngày nên ta có phương trình
\(\begin{array}{l}\dfrac{{261}}{{x + 3}} + 1 = \dfrac{{260}}{x} \Rightarrow 261x + x\left( {x + 3} \right) = 260\left( {x + 3} \right)\\ \Leftrightarrow 261x + {x^2} + 3x = 260x + 780\\ \Leftrightarrow {x^2} + 4x - 780 = 0\\ \Leftrightarrow {x^2} - 26x + 30x - 780 = 0\\ \Leftrightarrow x\left( {x - 26} \right) + 30\left( {x - 26} \right) = 0\\ \Leftrightarrow \left( {x - 26} \right)\left( {x + 30} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 26 = 0\\x + 30 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 26\,\,\,\left( {tm} \right)\\x = - 30\,\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy theo kế hoạch mỗi ngày nông trường khai thác \(26\) tấn mủ cao su.
Câu 4:
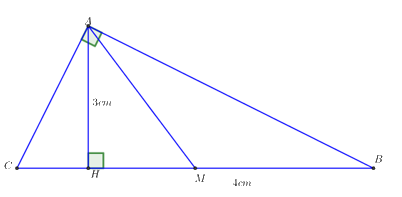
Cách giải:
+) Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
\(\,\,\,\,\,\,\,A{B^2} = A{H^2} + H{B^2} = {3^2} + {4^2} = 25 \Rightarrow AB = 5\,\,\,\left( {cm} \right)\).
+) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ABC với AH là đường cao ta có:
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} \Leftrightarrow \dfrac{1}{{A{C^2}}} = \dfrac{1}{{A{H^2}}} - \dfrac{1}{{A{B^2}}} \Leftrightarrow \dfrac{1}{{A{C^2}}} = \dfrac{1}{{{3^2}}} - \dfrac{1}{{{5^2}}} = \dfrac{{16}}{{225}} \Rightarrow AC = \dfrac{{15}}{4}\left( {cm} \right)\)
+) Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có:
\(B{C^2} = A{B^2} + A{C^2} = {5^2} + {\left( {\dfrac{{15}}{4}} \right)^2} = \dfrac{{625}}{{16}} \Rightarrow BC = \dfrac{{25}}{4}\left( {cm} \right)\).
+) Tam giác ABC vuông tại A có trung tuyến AM nên ta có: \(AM = \dfrac{1}{2}BC = \dfrac{{25}}{8}\,\,\,\left( {cm} \right)\)
+) Diện tích tam giác ABC với AH là đường cao ta có: \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.3.\dfrac{{25}}{4} = \dfrac{{75}}{8}\,\,\left( {c{m^2}} \right)\).
Vậy \(AB = 5cm,\,\,AC = \dfrac{{15}}{4}cm,\,\,AM = \dfrac{{25}}{8}cm,\,\,{S_{\Delta ABC}} = \dfrac{{75}}{8}\,\,c{m^2}\)
Câu 5:
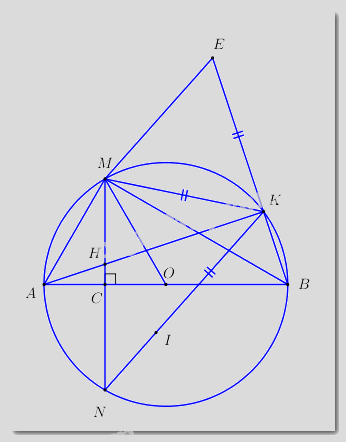
1) Chứng minh tứ giác \(BCHK\) là tứ giác nội tiếp.
Ta có: \(\angle AKB = {90^0}\) (góc nội tiếp chắn nửa đường tròn (O)) \( \Rightarrow \angle HKB = {90^0}\).
Có \(\angle ACH = \angle HCB = {90^0}\) (\(MN \bot AB;H;C \in MN\) )
Xét tứ giác \(BCHK\)có \(\angle HCB + \angle HKB = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(BCHK\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)).
2) Chứng minh \(AK.AH = {R^2}\).
Xét tam giác \(ACH\) và tam giác \(AKB\) có:
\(\angle BAK\) chung;
\(\angle ACH = \angle AKB = {90^0}\)(cmt)
.
3) Trên tia \(KN\) lấy điểm \(I\) sao cho \(KI = KM\). Chứng minh \(NI = BK\).
Trên tia đối của \(KB\) lấy điểm \(E\) sao cho \(KE = KM = KI\).
Xét tam giác \(OAM\) có đường cao \(MC\) đồng thời là trung tuyến \( \Rightarrow \Delta OAM\) cân tại \(M \Rightarrow OM = AM\).
Lại có \(OA = OM\,\, \Rightarrow \Delta OAM\) đều \( \Rightarrow \angle OAM = {60^0}\).
Ta có: \(\angle AMB = {90^0}\) (góc nội tiếp chắn nửa đường tròn). Do đó tam giác AMB vuông tại M
\( \Rightarrow \angle ABM = {30^0}\)
Xét tam giác vuông \(BCM\) có: \(\angle BMC = {90^0} - \angle ABM = {90^0} - {30^0} = {60^0} \Rightarrow \angle BMN = {60^0}\,\,\,\left( 1 \right)\)
Tứ giác \(ABKM\) là tứ giác nội tiếp \( \Rightarrow \angle EKM = \angle MAB = {60^0}\) (góc ngoài và góc trong tại đỉnh đối diện)
Lại có \(KE = KM\) (theo cách dựng) \( \Rightarrow \Delta MKE\) đều \( \Rightarrow \angle KME = {60^0}\,\,\left( 2 \right)\)
Từ (1) và (2)
\(\begin{array}{l} \Rightarrow \angle BMN = \angle KME = {60^0}\\ \Rightarrow \angle BMN + \angle BMK = \angle KME + \angle BMK\\ \Rightarrow \angle NMK = \angle BME\end{array}\)
Xét tam giác vuông \(BCM\) có: \(\sin \angle CBM = \sin {30^0} = \dfrac{{CM}}{{BM}} = \dfrac{1}{2} \Leftrightarrow BM = 2CM\).
Lại có \(OA \bot MN\) tại \(C \Rightarrow C\) là trung điểm của \(MN\) (quan hệ vuông góc giữa đường kíhn và dây cung)
\( \Rightarrow MN = 2CM\).
\( \Rightarrow MN = BM\,\,\left( { = 2CM} \right)\).
Xét tam giác \(MNK\) và tam giác \(BME\) có:
\(\angle MNK = \angle MBE\) (hai góc nội tiếp cùng chắn cung \(MK\));
\(\begin{array}{l}MN = BM\,\,\left( {cmt} \right);\\\angle NMK = \angle BME\,\,\left( {cmt} \right);\end{array}\)
\( \Rightarrow \Delta MNK = \Delta BME\,\,\left( {g.c.g} \right) \Rightarrow NK = BE\) (2 cạnh tương ứng).
\( \Rightarrow IN + IK = BK + KE\).
Mà \(IK = KE\) (theo cách vẽ) \( \Rightarrow IN = BK\,\,\left( {dpcm} \right)\).
Câu 1 (2 điểm):
1) Tính giá trị các biểu thức sau: \(A = 3\sqrt {49} - \sqrt {25} \)
2) Cho biểu thức: \(P = \left( {\dfrac{{\sqrt x }}{{\sqrt {x - 1} }} + \dfrac{{\sqrt x }}{{x - \sqrt x }}} \right):\dfrac{{\sqrt x + 1}}{3}\) với \(x > 0;\,\,x \ne 1\)
a) Rút gọn biểu thức \(P.\) b) Tìm giá trị của \(x\) để \(P = 1\)
Câu 2 (2,0 điểm):
1) Cho parabol \(\left( P \right)\) và đường thẳng \(\left( d \right):\,y = x + 2\)
a) Vẽ parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng một hệ trục tọa độ \(Oxy\)
b) Viết phương trình đường thẳng \(\left( {{d_1}} \right):\,y = ax + b\) song song với \(\left( d \right)\) và cắt \(\left( P \right)\) tại điểm \(A\) có hoành độ bằng \( - 2\) .
2) Không sử dụng máy tính, giải hệ phương trình: \(\left\{ \begin{array}{l}2x + y = 5\\x + 2y = 4\end{array} \right.\)
Câu 3 (2,5 điểm):
1) Cho phương trình: \({x^2} - \left( {m + 2} \right)x + m + 8 = 0\,\,\,\,\left( 1 \right)\) Với \(m\) là tham số.
a) Giải phương trình \(\left( 1 \right)\) khi \(m = - 8\)
b) Tìm các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm dương phân biệt \({x_1},\,{x_2}\) thỏa mãn hệ thức: \(x_1^3 - {x_2} = 0.\)
2) Nông trường cao su Minh Hưng phải khai thác 260 tấn mủ trong một thời gian nhất định. Trên thực tế, mỗi ngày nông trường đề khai thác vượt định mức 3 tấn. Do đó, nông trường đã khai thác được 26 tấn và xong trước thời hạn 1 ngày. Hỏi theo kế hoạch mỗi ngày nông trường khai thác được bao nhiêu tấn mủ cao su.
Câu 4 (1,0 điểm):
Cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\)và đường trung tuyến \(AM\). Biết \(AH = 3cm;\,HB = 4cm.\) Hãy tính \(AB,AC,AM\) và diện tích tam giác \(ABC.\)
Câu 5 (2,5 điểm):
Cho đường tròn tâm \(O\) đường kính \(AB = 2R.\) Gọi \(C\) là trung điểm của \(OA,\) qua \(C\) kẻ đường thẳng vuông góc với \(OA\) cắt đường tròn \(\left( O \right)\) tại hai điểm phân biệt \(M\) và \(N\) . Trên cung nhỏ \(BM\) lấy điểm \(K\) (\(K\) khác \(B\) và \(M\)). Gọi \(H\) là giao điểm của \(AK\) và \(MN.\)
a) Chứng minh tứ giác \(BCHK\) nội tiếp đường tròn.
b) Chứng minh \(AK.AH = {R^2}.\)
c) Trên tia \(KN\) lấy điểm \(I\) sao cho \(KI = KM.\) Chứng minh \(NI = BK.\)
Câu 1:
Phương pháp:
1) Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,A < 0\end{array} \right..\)
2) a) Quy đồng, rút gọn biểu thức.
b) Nhân chéo, giải tìm \(x\).
Cách giải:
1) Tính giá trị các biểu thức sau:
\(\begin{array}{l}A = 3\sqrt {49} - \sqrt {25} = 3\sqrt {{7^2}} - \sqrt {{5^2}} = 3.7 - 5 = 21 - 5 = 16\\B = \sqrt {{{\left( {3 - 2\sqrt 5 } \right)}^2}} - \sqrt {20} = \left| {3 - 2\sqrt 5 } \right| - \sqrt {{2^2}.5} = 2\sqrt 5 - 3 - 2\sqrt 5 = - 3\end{array}\)
2) Cho biểu thức \(P = \left( {\dfrac{{\sqrt x }}{{\sqrt x - 1}} + \dfrac{{\sqrt x }}{{x - \sqrt x }}} \right):\dfrac{{\sqrt x + 1}}{3}\) với \(x > 0,\,\,x \ne 1\).
a) Rút gọn biểu thức \(P\).
\(\begin{array}{l}P = \left( {\dfrac{{\sqrt x }}{{\sqrt x - 1}} + \dfrac{{\sqrt x }}{{x - \sqrt x }}} \right):\dfrac{{\sqrt x + 1}}{3} = \left( {\dfrac{{\sqrt x }}{{\sqrt x - 1}} + \dfrac{{\sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}}} \right):\dfrac{{\sqrt x + 1}}{3}\\\,\,\,\, = \dfrac{{x + \sqrt x }}{{\sqrt x \left( {\sqrt x - 1} \right)}}.\dfrac{3}{{\sqrt x + 1}} = \dfrac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\sqrt x \left( {\sqrt x - 1} \right)}}.\dfrac{3}{{\sqrt x + 1}}\\\,\,\,\, = \dfrac{3}{{\sqrt x - 1}}.\end{array}\)
Vậy \(P = \dfrac{3}{{\sqrt x - 1}}\).
b) Tìm giá trị của \(x\) để \(P = 1\).
\(P = 1 \Leftrightarrow \dfrac{3}{{\sqrt x - 1}} = 1 \Leftrightarrow \sqrt x - 1 = 3 \Leftrightarrow \sqrt x = 4 \Leftrightarrow x = 16\,\,\left( {tm} \right)\).
Vậy để \(P = 1\) thì \(x = 16\).
Câu 2:
Phương pháp:
Phương pháp:
1) a) Lập bảng giá trị, xác định các điểm đồ thị hàm số \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\) đi qua và vẽ đồ thị hàm số.
b) Đường thẳng \({d_1}:\,\,y = {a_1}x + {b_1}\) và \({d_2}:\,\,y = {a_2}x + {b_2}\) là hai đường thẳng song song với nhau \( \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\)
Tìm tọa độ giao điểm A của hai đồ thị hàm số \(\left( {{d_1}} \right)\) và \(\left( P \right)\) rồi thay vào phương trình \(\left( {{d_1}} \right)\) tìm \(b.\)
2) Giải hệ phương trình bằng phương pháp thế hoặc phương pháp cộng đại số.
Cách giải:
1) a) Vẽ parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) trên cùng một hệ trục tọa độ \(Oxy.\)
Ta có bảng giá trị:
+) Vẽ đồ thị hàm số \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\)
\(x\) | \( - 4\) | \( - 2\) | \(0\) | \(2\) | \(4\) |
\(y = \dfrac{1}{2}{x^2}\) | \(8\) | \(2\) | \(0\) | \(2\) | \(8\) |
Vậy đồ thị hàm số\(\left( P \right):\,\,\,y = \dfrac{1}{2}{x^2}\) là đường cong đi qua các điểm \(\left( { - 4;\,\,8} \right),\,\,\,\left( { - 2;\,\,2} \right),\,\,\,\left( {0;\,\,0} \right),\,\,\,\left( {2;\,\,2} \right),\,\,\,\left( {4;\,\,8} \right).\)
+) Vẽ đồ thị hàm số \(\left( d \right):\,\,\,y = x + 2:\)
\(x\) | \(0\) | \( - 2\) |
\(y = x + 2\) | \(2\) | \(0\) |
Đồ thị hàm số \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\) và \(\left( d \right):\,\,\,y = x + 2:\)
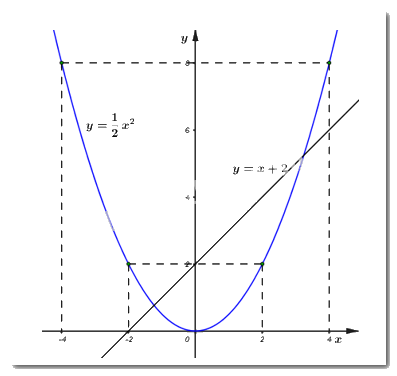
b) Viết phương trình đường thẳng \(\left( {{d_1}} \right):\,\,y = ax + b\) song song với \(\left( d \right)\) và cắt \(\left( P \right)\) tại điểm \(A\) có hoành độ bằng \( - 2.\)
Ta có đường thẳng \(\left( {{d_1}} \right):\,\,y = ax + b\) song song với đường thẳng \(\left( d \right):\,\,\,y = x + 2 \Rightarrow \left\{ \begin{array}{l}a = 1\\b \ne 2\end{array} \right..\)
\( \Rightarrow \left( {{d_1}} \right):\,\,\,y = x + b.\)
Gọi \(A\left( { - 2;\,\,{y_A}} \right)\) là giao điểm của đường thẳng \(\left( {{d_1}} \right)\) và đồ thị \(\left( P \right) \Rightarrow A \in \left( P \right)\)
\( \Rightarrow {y_A} = \dfrac{1}{2}.{\left( { - 2} \right)^2} = 2 \Rightarrow A\left( { - 2;\,\,2} \right).\)
Lại có \(A \in \left( {{d_1}} \right)\) nên thay \(x = - 2;y = 2\) vào phương trình đường thẳng \(\left( {{d_1}} \right):\,\,\,y = x + b\) ta được
\(2 = - 2 + b \Leftrightarrow b = 4\,\,\left( {tm} \right)\)
Vậy đường thẳng \(\left( {{d_1}} \right)\) có phương trình: \(y = x + 4.\)
2) Không sử dụng máy tính, giải hệ phương trình: \(\left\{ \begin{array}{l}2x + y = 5\\x + 2y = 4\end{array} \right..\)
\(\begin{array}{l}\left\{ \begin{array}{l}2x + y = 5\\x + 2y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 5 - 2x\\x + 2\left( {5 - 2x} \right) = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 5 - 2x\\x + 10 - 4x = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 5 - 2x\\3x = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 5 - 2.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right..\end{array}\)
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;\,\,y} \right) = \left( {2;\,\,1} \right).\)
Câu 3:
Phương pháp:
1) a) Thay \(m\) và phương trình và giải phương trình bậc hai ẩn \(x\).
b) + Phương trình \(\left( 1 \right)\) có hai nghiệm dương phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta > 0\\S > 0\\P > 0\end{array} \right.\)
+ Rút \({x_2} = x_1^2\) thay vào điều kiện \({x_1}{x_2} = \dfrac{c}{a}\) tìm nghiệm \({x_1},{x_2}\).
+ Thay \({x_1},{x_2}\) tìm được ở trên vào \({x_1} + {x_2} = - \dfrac{b}{a}\) tìm \(m\).
2) Giải bài toán bằng cách lập phương trình
Bước 1: Chọn ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết. Lập phương trình
Bước 3: Giải phương trình rồi so sánh với điều kiện để chọn ra các giá trị thích hợp và kết luận.
Cách giải:
1) a) Thay \(m = - 8\) vào phương trình \(\left( 1 \right)\) ta được:
\({x^2} - \left( { - 8 + 2} \right)x + \left( { - 8} \right) + 8 = 0 \Leftrightarrow {x^2} + 6x = 0 \Leftrightarrow x\left( {x + 6} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 6\end{array} \right.\).
Vậy với \(m = - 8\) thì phương trình có tập nghiệm \(S = \left\{ {0; - 6} \right\}.\)
b) Phương trình \(\left( 1 \right)\) có hai nghiệm dương phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}a = 1 \ne 0\\\Delta > 0\\S > 0\\P > 0\end{array} \right.\)
Có \(\Delta {\rm{ = }}{\left( {m + 2} \right)^2} - 4\left( {m + 8} \right) = {m^2} + 4m + 4 - 4m - 32 > 0 \Leftrightarrow {m^2} - 28 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 2\sqrt 7 \\m < - 2\sqrt 7 \end{array} \right.\,\,\,\,\,\,\left( 1 \right)\).
\(S = - \dfrac{b}{a} = m + 2 > 0 \Leftrightarrow m > - 2\,\,\,\,\,\,\left( 2 \right)\).
\(P = \dfrac{c}{a} = m + 8 > 0 \Leftrightarrow m > - 8\,\,\,\,\,\left( 3 \right)\).
Kết hợp các điều kiện (1), (2), (3) ta được \(\left[ \begin{array}{l}m > 2\sqrt 7 \\ - 8 < m < 2\sqrt 7 \end{array} \right..\)
Theo bài ra ta có:
\(\begin{array}{l}x_1^3 - {x_2} = 0 \Leftrightarrow x_1^3 = {x_2} \Leftrightarrow {x_1}{x_2} = x_1^4 = m + 8 \Leftrightarrow {x_1} = \sqrt[4]{{m + 8}} \Rightarrow {x_2} = \sqrt[4]{{{{\left( {m + 8} \right)}^3}}}\\ \Rightarrow {x_1} + {x_2} = m + 2 \Leftrightarrow \sqrt[4]{{m + 8}} + \sqrt[4]{{{{\left( {m + 8} \right)}^3}}} = m + 8 - 6\end{array}\)
Đặt \(\sqrt[4]{{m + 8}} = t\,\,\left( {t \ge 0} \right)\), ta có
\(\begin{array}{l}\,\,\,\,\,\,\,t + {t^3} = {t^4} - 6\\ \Leftrightarrow {t^4} - {t^3} - t - 6 = 0\\ \Leftrightarrow {t^4} - 16 - \left( {{t^3} + t - 10} \right) = 0\\ \Leftrightarrow \left( {{t^2} - 4} \right)\left( {{t^2} + 4} \right) - \left( {{t^3} - 8 + t - 2} \right) = 0\\ \Leftrightarrow \left( {t - 2} \right)\left( {t + 2} \right)\left( {{t^2} + 4} \right) - \left[ {\left( {t - 2} \right)\left( {{t^2} + 2t + 4} \right) + \left( {t - 2} \right)} \right] = 0\\ \Leftrightarrow \left( {t - 2} \right)\left( {t + 2} \right)\left( {{t^2} + 4} \right) - \left( {t - 2} \right)\left( {{t^2} + 2t + 5} \right) = 0\\ \Leftrightarrow \left( {t - 2} \right)\left( {{t^3} + 2{t^2} + 4t + 8 - {t^2} - 2t - 5} \right) = 0\\ \Leftrightarrow \left( {t - 2} \right)\left( {{t^3} + {t^2} + 2t + 3} \right) = 0\\ \Leftrightarrow t = 2\,\,\left( {Do\,\,\,t \ge 0 \Rightarrow {t^3} + {t^2} + 2t + 3 > 0} \right)\end{array}\)
\( \Rightarrow \sqrt[4]{{m + 8}} = 2 \Leftrightarrow m + 8 = {2^4} = 16 \Leftrightarrow m = 8\,\,\left( {tm} \right)\).
Vậy \(m = 8\).
2) Gọi số tấn mủ cao su mỗi ngày nông trường khai thác được là \(x\) tấn \(\left( {0 < x < 260} \right)\)
\( \Rightarrow \) Thời gian theo dự định khai thác mủ cao su của nông trường là \(\dfrac{{260}}{x}\) (ngày)
Theo thực tế mỗi ngày nông trường khai thác được số tấn mủ cao su là: \(x + 3\) (tấn)
\( \Rightarrow \) Thời gian theo thực tế khai thác mủ cao su của nông trường là \(\dfrac{{261}}{{x + 3}}\) (ngày)
Vì nông trường khai thác xong trước thời hạn 1 ngày nên ta có phương trình
\(\begin{array}{l}\dfrac{{261}}{{x + 3}} + 1 = \dfrac{{260}}{x} \Rightarrow 261x + x\left( {x + 3} \right) = 260\left( {x + 3} \right)\\ \Leftrightarrow 261x + {x^2} + 3x = 260x + 780\\ \Leftrightarrow {x^2} + 4x - 780 = 0\\ \Leftrightarrow {x^2} - 26x + 30x - 780 = 0\\ \Leftrightarrow x\left( {x - 26} \right) + 30\left( {x - 26} \right) = 0\\ \Leftrightarrow \left( {x - 26} \right)\left( {x + 30} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 26 = 0\\x + 30 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 26\,\,\,\left( {tm} \right)\\x = - 30\,\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy theo kế hoạch mỗi ngày nông trường khai thác \(26\) tấn mủ cao su.
Câu 4:
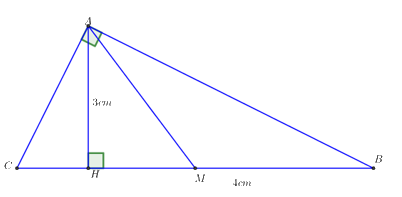
Cách giải:
+) Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
\(\,\,\,\,\,\,\,A{B^2} = A{H^2} + H{B^2} = {3^2} + {4^2} = 25 \Rightarrow AB = 5\,\,\,\left( {cm} \right)\).
+) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ABC với AH là đường cao ta có:
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} \Leftrightarrow \dfrac{1}{{A{C^2}}} = \dfrac{1}{{A{H^2}}} - \dfrac{1}{{A{B^2}}} \Leftrightarrow \dfrac{1}{{A{C^2}}} = \dfrac{1}{{{3^2}}} - \dfrac{1}{{{5^2}}} = \dfrac{{16}}{{225}} \Rightarrow AC = \dfrac{{15}}{4}\left( {cm} \right)\)
+) Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có:
\(B{C^2} = A{B^2} + A{C^2} = {5^2} + {\left( {\dfrac{{15}}{4}} \right)^2} = \dfrac{{625}}{{16}} \Rightarrow BC = \dfrac{{25}}{4}\left( {cm} \right)\).
+) Tam giác ABC vuông tại A có trung tuyến AM nên ta có: \(AM = \dfrac{1}{2}BC = \dfrac{{25}}{8}\,\,\,\left( {cm} \right)\)
+) Diện tích tam giác ABC với AH là đường cao ta có: \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.3.\dfrac{{25}}{4} = \dfrac{{75}}{8}\,\,\left( {c{m^2}} \right)\).
Vậy \(AB = 5cm,\,\,AC = \dfrac{{15}}{4}cm,\,\,AM = \dfrac{{25}}{8}cm,\,\,{S_{\Delta ABC}} = \dfrac{{75}}{8}\,\,c{m^2}\)
Câu 5:
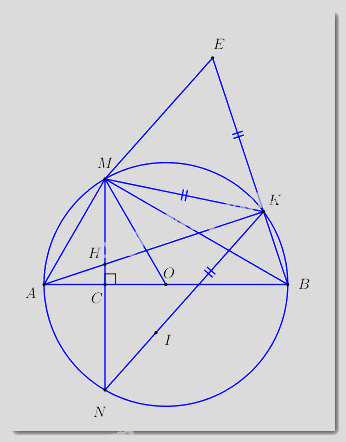
1) Chứng minh tứ giác \(BCHK\) là tứ giác nội tiếp.
Ta có: \(\angle AKB = {90^0}\) (góc nội tiếp chắn nửa đường tròn (O)) \( \Rightarrow \angle HKB = {90^0}\).
Có \(\angle ACH = \angle HCB = {90^0}\) (\(MN \bot AB;H;C \in MN\) )
Xét tứ giác \(BCHK\)có \(\angle HCB + \angle HKB = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(BCHK\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)).
2) Chứng minh \(AK.AH = {R^2}\).
Xét tam giác \(ACH\) và tam giác \(AKB\) có:
\(\angle BAK\) chung;
\(\angle ACH = \angle AKB = {90^0}\)(cmt)
.
3) Trên tia \(KN\) lấy điểm \(I\) sao cho \(KI = KM\). Chứng minh \(NI = BK\).
Trên tia đối của \(KB\) lấy điểm \(E\) sao cho \(KE = KM = KI\).
Xét tam giác \(OAM\) có đường cao \(MC\) đồng thời là trung tuyến \( \Rightarrow \Delta OAM\) cân tại \(M \Rightarrow OM = AM\).
Lại có \(OA = OM\,\, \Rightarrow \Delta OAM\) đều \( \Rightarrow \angle OAM = {60^0}\).
Ta có: \(\angle AMB = {90^0}\) (góc nội tiếp chắn nửa đường tròn). Do đó tam giác AMB vuông tại M
\( \Rightarrow \angle ABM = {30^0}\)
Xét tam giác vuông \(BCM\) có: \(\angle BMC = {90^0} - \angle ABM = {90^0} - {30^0} = {60^0} \Rightarrow \angle BMN = {60^0}\,\,\,\left( 1 \right)\)
Tứ giác \(ABKM\) là tứ giác nội tiếp \( \Rightarrow \angle EKM = \angle MAB = {60^0}\) (góc ngoài và góc trong tại đỉnh đối diện)
Lại có \(KE = KM\) (theo cách dựng) \( \Rightarrow \Delta MKE\) đều \( \Rightarrow \angle KME = {60^0}\,\,\left( 2 \right)\)
Từ (1) và (2)
\(\begin{array}{l} \Rightarrow \angle BMN = \angle KME = {60^0}\\ \Rightarrow \angle BMN + \angle BMK = \angle KME + \angle BMK\\ \Rightarrow \angle NMK = \angle BME\end{array}\)
Xét tam giác vuông \(BCM\) có: \(\sin \angle CBM = \sin {30^0} = \dfrac{{CM}}{{BM}} = \dfrac{1}{2} \Leftrightarrow BM = 2CM\).
Lại có \(OA \bot MN\) tại \(C \Rightarrow C\) là trung điểm của \(MN\) (quan hệ vuông góc giữa đường kíhn và dây cung)
\( \Rightarrow MN = 2CM\).
\( \Rightarrow MN = BM\,\,\left( { = 2CM} \right)\).
Xét tam giác \(MNK\) và tam giác \(BME\) có:
\(\angle MNK = \angle MBE\) (hai góc nội tiếp cùng chắn cung \(MK\));
\(\begin{array}{l}MN = BM\,\,\left( {cmt} \right);\\\angle NMK = \angle BME\,\,\left( {cmt} \right);\end{array}\)
\( \Rightarrow \Delta MNK = \Delta BME\,\,\left( {g.c.g} \right) \Rightarrow NK = BE\) (2 cạnh tương ứng).
\( \Rightarrow IN + IK = BK + KE\).
Mà \(IK = KE\) (theo cách vẽ) \( \Rightarrow IN = BK\,\,\left( {dpcm} \right)\).
Kỳ thi tuyển sinh vào lớp 10 là một bước ngoặt quan trọng trong quá trình học tập của mỗi học sinh. Để đạt kết quả tốt nhất, việc chuẩn bị kỹ lưỡng là vô cùng cần thiết. Đề thi vào 10 môn Toán Bình Phước năm 2019 là một nguồn tài liệu quý giá để các em học sinh có thể làm quen với cấu trúc đề thi, dạng bài tập và rèn luyện kỹ năng giải toán.
Đề thi vào 10 môn Toán Bình Phước năm 2019 thường bao gồm các dạng bài tập sau:
Phương trình bậc hai là một trong những dạng bài tập cơ bản và thường xuyên xuất hiện trong đề thi vào 10. Để giải phương trình bậc hai, các em có thể sử dụng các phương pháp sau:
Các bài toán chứng minh đẳng thức hình học đòi hỏi các em phải nắm vững các định lý và tính chất hình học cơ bản. Để chứng minh đẳng thức hình học, các em có thể sử dụng các phương pháp sau:
Để đạt kết quả tốt nhất trong kỳ thi vào 10 môn Toán, các em nên:
Giaitoan.edu.vn là một nền tảng học toán online uy tín, cung cấp các khóa học chất lượng cao, bài giảng chi tiết, và đề thi thử đa dạng. Chúng tôi cam kết đồng hành cùng bạn trên con đường chinh phục kiến thức và đạt được thành công trong kỳ thi vào 10 môn Toán Bình Phước năm 2019.
Ngoài đề thi vào 10 môn Toán Bình Phước năm 2019, các em có thể tham khảo thêm các tài liệu sau:
Đề thi vào 10 môn Toán Bình Phước năm 2019 là một tài liệu quan trọng để các em học sinh có thể chuẩn bị cho kỳ thi tuyển sinh vào lớp 10. Hy vọng rằng với những phân tích và hướng dẫn giải chi tiết trong bài viết này, các em sẽ tự tin hơn và đạt kết quả tốt nhất trong kỳ thi sắp tới.