Chào mừng các em học sinh đến với đề tham khảo thi vào 10 môn Toán TP Hồ Chí Minh năm 2025 - Đề số 2 của giaitoan.edu.vn. Đề thi này được biên soạn dựa trên cấu trúc đề thi tuyển sinh vào 10 của các trường THPT chuyên và không chuyên tại TP.HCM, giúp các em làm quen với dạng đề và rèn luyện kỹ năng giải toán.
Đề thi bao gồm các câu hỏi trắc nghiệm và tự luận, tập trung vào các kiến thức trọng tâm của chương trình Toán lớp 9.
Câu 1 (1,5 điểm): Cho hàm số (left( P right):y = - frac{{{x^2}}}{4}). a) Vẽ đồ thị (left( P right)) của hàm số trên. b) Tìm trên (left( P right)) những điểm có tung độ gấp (3) lần hoành độ.
Câu 1 (1,5 điểm): Cho hàm số \(\left( P \right):y = - \frac{{{x^2}}}{4}\).
a) Vẽ đồ thị \(\left( P \right)\) của hàm số trên.
b) Tìm trên \(\left( P \right)\) những điểm có tung độ gấp \(3\) lần hoành độ.
Câu 2 (1 điểm): Cho phương trình \(4{x^2} + 4x - 3 = 0\)
a) Không giải phương trình, chứng minh phương trình luôn có hai nghiệm phân biệt.
b) Tính giá trị biểu thức \(A = {x_1}\left( {4 + \frac{1}{3}{x_2}} \right) + 4{x_2}\).
Câu 3 (1,5 điểm): Biểu đồ cột kép dưới đây biểu diễn lượng mưa trung bình (đơn vị: mm) của các tháng trong một năm ở Hà Nội và Thành phố Hồ Chí Minh.
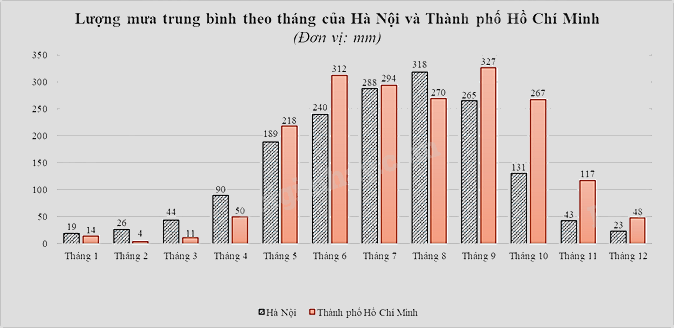
a) Tính lượng mưa chênh lệch trung bình ở hai địa điểm Hà Nội và Thành phố Hồ Chí Minh.
b) Chọn ngẫu nhiên một tháng trong năm, tính xác suất của các biến cố sau:
\(P\): “Lượng mưa trung bình của Thành phố Hồ Chí Minh lớn hơn \(200\)mm”
\(Q\): “Lượng mưa chênh lệch của Hà Nội và Thành phố Hồ Chí Minh không vượt quá \(40\)mm”
Câu 4 (1 điểm): Ông An có một mảnh đất hình chữ nhật có chiều rộng là 8 m và chiều dài là 20 m. Nhà nước làm một con đường đi ngang qua mảnh đất của ông An và thu hồi một phần đất của ông An (phần hình tam giác). Phần đất không bị thu hồi có kích thước như hình vẽ dưới (phần tô đậm).
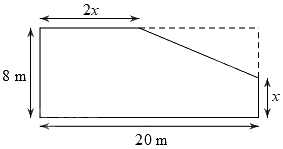
a) Viết biểu thức (thu gọn) T biểu thị theo \(x\) (với \(0 < x < 8\)) diện tích đất bị thu hồi của nhà ông An.
b) Ông An được đền bù số tiền 455 triệu đồng cho diện tích đất bị thu hồi. Tìm giá trị \(x\)(m) biết giá đền bù đất bị thu hồi là 13 triệu đồng\(/{m^2}\).
Câu 5 (1 điểm): Hiện nay, người ta thường dùng chất liệu PVC (polyvinylchloride) để chế tạo vỏ quả bóng cao su dùng trong bóng đá. Một quả bóng hình cầu thường sử dụng từ hai đến bốn lớp vải lót để làm vỏ bóng và một quả bóng đá thường có chu vi đường tròn lớn từ \(58 - 71\)cm tuỳ vào kích thước bóng để phù hợp cho từng lứa tuổi. Bác Minh có một quả bóng đá size số 7 có chu vi \(70\)cm và vỏ quả bóng được tạo thành từ 4 lớp vải lót có độ dày \(2,5\)mm (xem hình ảnh minh hoạ).

a) Tính thể tích không khí tối đa bên trong quả bóng khi quả bóng căng tròn.
b) Sau một thời gian sử dụng, quả bóng không còn chất lượng như ban đầu nên bác Minh cắt quả bóng theo mặt cắt là một đường tròn để tái chế quả bóng thành một chậu cây có dạng như ảnh minh hoạ. Bác Minh dùng dụng cụ xúc đất như hình trên để xúc đất vào quả bóng, biết thể tích dụng cụ xúc đất bằng \(70\% \) thể tích hình trụ có cùng bán kính đáy, chiều cao. Thể tích đất bác Minh cần bỏ vào quả bóng bằng \(\frac{4}{5}\) thể tích quả bóng ban đầu. Hỏi bác Minh cần xúc ít nhất bao nhiêu lần, biết mỗi lần xúc được một thể tích đất bằng thể tích dụng cụ xúc?

(Lấy \(\pi \approx 3,14\), làm tròn kết quả đến hàng phần trăm)
Câu 6 (1 điểm): Cách Tết Trung thu 1 tháng, bà Hoa nhập 100 cái bánh dẻo đậu xanh và 150 cái bánh nướng thập cẩm hết 10 230 000 đồng. Thấy bán được, bà Hoa nhập thêm 400 cái bánh dẻo đậu xanh và 200 cái bánh nướng thập cẩm (cùng giá nhập đợt đầu) hết 22 920 000 đồng.
a) Hỏi giá nhập của mỗi chiếc bánh dẻo đậu xanh và bánh nướng thập cẩm là bao nhiêu?
b) Trước Tết Trung thu 3 ngày, bà Hoa đã bán hết bánh nướng thập cẩm nhưng vẫn còn 100 cái bánh dẻo đậu xanh. Để nhanh chóng bán hết số bánh đã nhập về, bà Hoa thực hiện chương trình khuyến mại như sau: mua cái bánh thứ nhất bằng giá niêm yết, cái bánh thứ hai giảm 30% so với giá niêm yết, cái bánh thứ ba trở đi giảm 60% so với giá niêm yết. Bạn Mai đến cửa hàng bà Hoa mua 5 cái bánh dẻo đậu xanh phải trả 145 000 đồng. Hỏi giá niêm yết của mỗi cái bánh dẻo đậu xanh là bao nhiêu?
Câu 7 (3 điểm): Cho đường tròn tâm \(O\) đường kính \(BC\), điểm \(A\) nằm ngoài đường tròn sao cho \(\widehat {BAC} < 90^\circ \). Gọi \(M,\,N\) là giao điểm của \(AB\) và \(AC\) với đường tròn \(\left( O \right)\) (\(M\) khác \(B\), \(N\) khác \(C\)). Hai đường thẳng \(BN\) và \(CM\) cắt nhau tại \(I\).
a) Chứng minh \(AI \bot BC\) và tứ giác \(MANI\) là tứ giác nội tiếp.
b) Gọi \(D\) là điểm trên cung nhỏ \(MN\) sao cho $\overset\frown{MD}=\overset\frown{ND}$, \(P\) là giao điểm của \(BD\) và \(CM\), \(Q\) là giao điểm của \(CD\) và \(BN\). Chứng minh rằng \(DQ.CD = BD.DP\) và \(\widehat {IPD} = \widehat {IQD}\).
c) Giả sử \(\widehat {BAC} = 60^\circ \) và \(BC = 10\)cm. Tính độ dài \(MN\) và chu vi đường tròn ngoại tiếp \(\Delta MIN\). (lấy \(\pi \approx 3,14\))
-------- HẾT --------
Tải về
Câu 1 (1,5 điểm): Cho hàm số \(\left( P \right):y = - \frac{{{x^2}}}{4}\).
a) Vẽ đồ thị \(\left( P \right)\) của hàm số trên.
b) Tìm trên \(\left( P \right)\) những điểm có tung độ gấp \(3\) lần hoành độ.
Câu 2 (1 điểm): Cho phương trình \(4{x^2} + 4x - 3 = 0\)
a) Không giải phương trình, chứng minh phương trình luôn có hai nghiệm phân biệt.
b) Tính giá trị biểu thức \(A = {x_1}\left( {4 + \frac{1}{3}{x_2}} \right) + 4{x_2}\).
Câu 3 (1,5 điểm): Biểu đồ cột kép dưới đây biểu diễn lượng mưa trung bình (đơn vị: mm) của các tháng trong một năm ở Hà Nội và Thành phố Hồ Chí Minh.
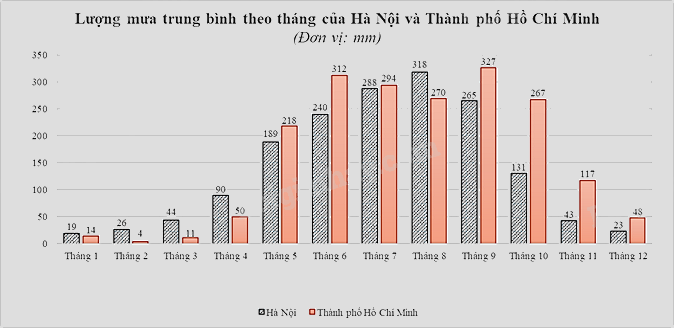
a) Tính lượng mưa chênh lệch trung bình ở hai địa điểm Hà Nội và Thành phố Hồ Chí Minh.
b) Chọn ngẫu nhiên một tháng trong năm, tính xác suất của các biến cố sau:
\(P\): “Lượng mưa trung bình của Thành phố Hồ Chí Minh lớn hơn \(200\)mm”
\(Q\): “Lượng mưa chênh lệch của Hà Nội và Thành phố Hồ Chí Minh không vượt quá \(40\)mm”
Câu 4 (1 điểm): Ông An có một mảnh đất hình chữ nhật có chiều rộng là 8 m và chiều dài là 20 m. Nhà nước làm một con đường đi ngang qua mảnh đất của ông An và thu hồi một phần đất của ông An (phần hình tam giác). Phần đất không bị thu hồi có kích thước như hình vẽ dưới (phần tô đậm).
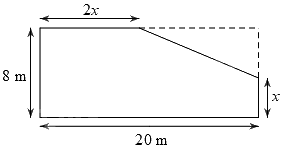
a) Viết biểu thức (thu gọn) T biểu thị theo \(x\) (với \(0 < x < 8\)) diện tích đất bị thu hồi của nhà ông An.
b) Ông An được đền bù số tiền 455 triệu đồng cho diện tích đất bị thu hồi. Tìm giá trị \(x\)(m) biết giá đền bù đất bị thu hồi là 13 triệu đồng\(/{m^2}\).
Câu 5 (1 điểm): Hiện nay, người ta thường dùng chất liệu PVC (polyvinylchloride) để chế tạo vỏ quả bóng cao su dùng trong bóng đá. Một quả bóng hình cầu thường sử dụng từ hai đến bốn lớp vải lót để làm vỏ bóng và một quả bóng đá thường có chu vi đường tròn lớn từ \(58 - 71\)cm tuỳ vào kích thước bóng để phù hợp cho từng lứa tuổi. Bác Minh có một quả bóng đá size số 7 có chu vi \(70\)cm và vỏ quả bóng được tạo thành từ 4 lớp vải lót có độ dày \(2,5\)mm (xem hình ảnh minh hoạ).

a) Tính thể tích không khí tối đa bên trong quả bóng khi quả bóng căng tròn.
b) Sau một thời gian sử dụng, quả bóng không còn chất lượng như ban đầu nên bác Minh cắt quả bóng theo mặt cắt là một đường tròn để tái chế quả bóng thành một chậu cây có dạng như ảnh minh hoạ. Bác Minh dùng dụng cụ xúc đất như hình trên để xúc đất vào quả bóng, biết thể tích dụng cụ xúc đất bằng \(70\% \) thể tích hình trụ có cùng bán kính đáy, chiều cao. Thể tích đất bác Minh cần bỏ vào quả bóng bằng \(\frac{4}{5}\) thể tích quả bóng ban đầu. Hỏi bác Minh cần xúc ít nhất bao nhiêu lần, biết mỗi lần xúc được một thể tích đất bằng thể tích dụng cụ xúc?

(Lấy \(\pi \approx 3,14\), làm tròn kết quả đến hàng phần trăm)
Câu 6 (1 điểm): Cách Tết Trung thu 1 tháng, bà Hoa nhập 100 cái bánh dẻo đậu xanh và 150 cái bánh nướng thập cẩm hết 10 230 000 đồng. Thấy bán được, bà Hoa nhập thêm 400 cái bánh dẻo đậu xanh và 200 cái bánh nướng thập cẩm (cùng giá nhập đợt đầu) hết 22 920 000 đồng.
a) Hỏi giá nhập của mỗi chiếc bánh dẻo đậu xanh và bánh nướng thập cẩm là bao nhiêu?
b) Trước Tết Trung thu 3 ngày, bà Hoa đã bán hết bánh nướng thập cẩm nhưng vẫn còn 100 cái bánh dẻo đậu xanh. Để nhanh chóng bán hết số bánh đã nhập về, bà Hoa thực hiện chương trình khuyến mại như sau: mua cái bánh thứ nhất bằng giá niêm yết, cái bánh thứ hai giảm 30% so với giá niêm yết, cái bánh thứ ba trở đi giảm 60% so với giá niêm yết. Bạn Mai đến cửa hàng bà Hoa mua 5 cái bánh dẻo đậu xanh phải trả 145 000 đồng. Hỏi giá niêm yết của mỗi cái bánh dẻo đậu xanh là bao nhiêu?
Câu 7 (3 điểm): Cho đường tròn tâm \(O\) đường kính \(BC\), điểm \(A\) nằm ngoài đường tròn sao cho \(\widehat {BAC} < 90^\circ \). Gọi \(M,\,N\) là giao điểm của \(AB\) và \(AC\) với đường tròn \(\left( O \right)\) (\(M\) khác \(B\), \(N\) khác \(C\)). Hai đường thẳng \(BN\) và \(CM\) cắt nhau tại \(I\).
a) Chứng minh \(AI \bot BC\) và tứ giác \(MANI\) là tứ giác nội tiếp.
b) Gọi \(D\) là điểm trên cung nhỏ \(MN\) sao cho $\overset\frown{MD}=\overset\frown{ND}$, \(P\) là giao điểm của \(BD\) và \(CM\), \(Q\) là giao điểm của \(CD\) và \(BN\). Chứng minh rằng \(DQ.CD = BD.DP\) và \(\widehat {IPD} = \widehat {IQD}\).
c) Giả sử \(\widehat {BAC} = 60^\circ \) và \(BC = 10\)cm. Tính độ dài \(MN\) và chu vi đường tròn ngoại tiếp \(\Delta MIN\). (lấy \(\pi \approx 3,14\))
-------- HẾT --------
Câu 1 (1,5 điểm): Cho hàm số \(\left( P \right):y = - \frac{{{x^2}}}{4}\).
a) Vẽ đồ thị \(\left( P \right)\) của hàm số trên.
b) Tìm trên \(\left( P \right)\) những điểm có tung độ gấp \(3\) lần hoành độ.
Phương pháp
a) Lập bảng giá trị, vẽ đồ thị hàm số trên hệ trục tọa độ.
b) Gọi điểm thuộc \(\left( P \right)\) có tung độ gấp \(3\) lần hoành độ có toạ độ là \(\left( {{x_0};3{x_0}} \right)\).
Thay \({y_0} = 3{x_0}\) vào hàm số và giải phương trình đưa về phương trình tích.
Lời giải
a) Ta có bảng giá trị:

Đồ thị \(\left( P \right)\) của hàm số là đường cong parabol đi qua các điểm
\(O\,\left( {0;0} \right);A\left( { - 2; - 1} \right);B\left( { - 1; - \frac{1}{4}} \right);\,\,C\left( {1; - \frac{1}{4}} \right);\,\,D\left( {2; - 1} \right)\)
Ta vẽ được đồ thị hàm số \(y = - \frac{{{x^2}}}{4}\) như sau:
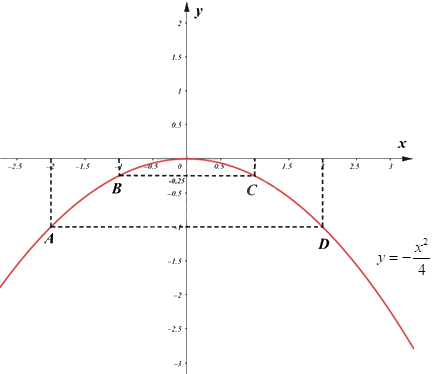
b) Gọi điểm thuộc \(\left( P \right)\) có tung độ gấp \(3\) lần hoành độ có toạ độ là \(\left( {{x_0};3{x_0}} \right)\).
Vì điểm nằm trên đồ thị của hàm số \(y = - \frac{{{x^2}}}{4}\) nên ta có:
\(\begin{array}{l}3{x_0} = - \frac{{x_0^2}}{4}\\12{x_0} = - x_0^2\\x_0^2 + 12{x_0} = 0\\{x_0}\left( {{x_0} + 12} \right) = 0\end{array}\)
Suy ra \({x_0} = 0\) hoặc \({x_0} = - 12\).
Vậy những điểm có tung độ gấp \(3\) lần hoành độ trên \(\left( P \right)\) là \(\left( {0;0} \right)\) và \(\left( { - 12; - 36} \right)\).
Câu 2 (1 điểm): Cho phương trình \(4{x^2} + 4x - 3 = 0\)
a) Không giải phương trình, chứng minh phương trình luôn có hai nghiệm phân biệt.
b) Tính giá trị biểu thức \(A = {x_1}\left( {4 + \frac{1}{3}{x_2}} \right) + 4{x_2}\).
Phương pháp
a) Kiểm tra nghiệm của phương trình theo \(a.c\).
b) Áp dụng định lí Viète và biến đổi.
Định lí Viète: \({x_1} + {x_2} = \frac{{ - b}}{a};{x_1}{x_2} = \frac{c}{a}\)
Lời giải
a) Phương trình \(4{x^2} + 4x - 3 = 0\) có:
\(a.c = 4.\left( { - 3} \right) = - 12 < 0\) nên phương trình có hai nghiệm phân biệt \({x_1},{x_2}\).
b) Áp dụng định lí Viète, ta có:
\(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - 4}}{4} = - 1}\\{{x_1}{x_2} = \frac{{ - 3}}{4}}\end{array}} \right.\)
Ta có: \(A = {x_1}\left( {4 + \frac{1}{3}{x_2}} \right) + 4{x_2}\)
\(\begin{array}{l} = 4{x_1} + \frac{1}{3}{x_1}{x_2} + 4{x_2}\\ = 4({x_1} + {x_2}) + \frac{1}{3}{x_1}{x_2}\\ = 4.( - 1) + \frac{1}{3}.\left( { - \frac{3}{4}} \right)\\ = - \frac{{17}}{4}\end{array}\)
Vậy \(A = - \frac{{17}}{4}\).
Câu 3 (1,5 điểm): Biểu đồ cột kép dưới đây biểu diễn lượng mưa trung bình (đơn vị: mm) của các tháng trong một năm ở Hà Nội và Thành phố Hồ Chí Minh.
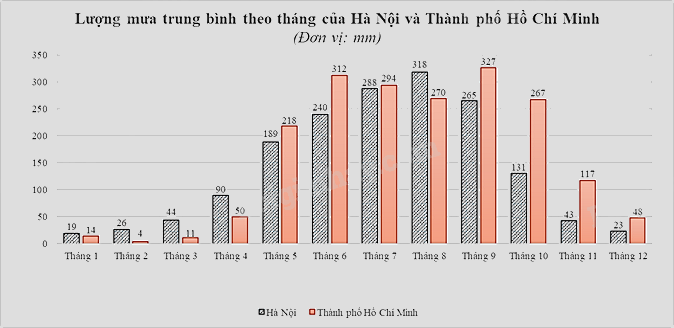
a) Tính lượng mưa chênh lệch trung bình ở hai địa điểm Hà Nội và Thành phố Hồ Chí Minh.
b) Chọn ngẫu nhiên một tháng trong năm, tính xác suất của các biến cố sau:
\(P\): “Lượng mưa trung bình của Thành phố Hồ Chí Minh lớn hơn \(200\)mm”
\(Q\): “Lượng mưa chênh lệch của Hà Nội và Thành phố Hồ Chí Minh không vượt quá \(40\)mm”
Phương pháp
a) Quan sát biểu đồ, xác định lượng mưa chênh lệch ở hai địa điểm Hà Nội và Thành phố Hồ Chí Minh theo từng tháng = giá trị lớn hơn – giá trị nhỏ hơn.
Lượng mưa chênh lệch trung bình = tổng lượng lượng mưa chênh lệch của 12 tháng : 12 tháng.
b) Xác định số phần tử của không gian mẫu, biến cố P và Q, từ đó tính xác suất của biến cố = số phần tử của biến cố : số phần tử của không gian mẫu.
Lời giải
a)Lượng mưa chênh lệch ở hai địa điểm Hà Nội và Thành phố Hồ Chí Minh theo từng tháng là:
Tháng 1: \(19 - 14 = 5\)
Tháng 2: \(26 - 4 = 22\)
Tháng 3: \(44 - 11 = 33\)
Tháng 4: \(90 - 50 = 40\)
Tháng 5: \(218 - 189 = 29\)
Tháng 6: \(312 - 240 = 72\)
Tháng 7: \(294 - 288 = 6\)
Tháng 8: \(318 - 270 = 48\)
Tháng 9: \(327 - 265 = 62\)
Tháng 10: \(267 - 131 = 136\)
Tháng 11: \(117 - 43 = 74\)
Tháng 12: \(48 - 23 = 25\)
Lượng mưa chênh lệch trung bình là:
\(\frac{{5 + 22 + 33 + 40 + 29 + 72 + 6 + 48 + 62 + 136 + 74 + 25}}{{12}} = 46\)(mm)
b) Không gian mẫu có số phần tử là 12.
Xét biến cố \(P\): “Lượng mưa trung bình của Thành phố Hồ Chí Minh lớn hơn \(200\)mm”.
Số tháng được chọn có lượng mưa trung bình của Thành phố Hồ Chí Minh lớn hơn \(200\)mm là \(6\) tháng: tháng 5, 6, 7, 8, 9, 10.
Suy ra số phần tử của biến cố \(P\) là 6.
Vậy xác suất của biến cố \(P\) là: \(p\left( P \right)=\frac{6}{12}=\frac{1}{2}\).
Xét biến cố \(Q\): “Lượng mưa chênh lệch của Hà Nội và Thành phố Hồ Chí Minh không vượt quá \(40\)mm”.
Số tháng được chọn có lượng mưa chênh lệch của Hà Nội và Thành phố Hồ Chí Minh không vượt quá \(40\)mm là \(7\) tháng: tháng 1; 2; 3; 4; 5; 7; 12.
Suy ra số phần tử của biến cố \(Q\) là \(7\).
Vậy xác suất của biến cố \(Q\) là: \(p\left( Q \right)=\frac{7}{12}\).
Câu 4 (1 điểm): Ông An có một mảnh đất hình chữ nhật có chiều rộng là 8 m và chiều dài là 20 m. Nhà nước làm một con đường đi ngang qua mảnh đất của ông An và thu hồi một phần đất của ông An (phần hình tam giác). Phần đất không bị thu hồi có kích thước như hình vẽ dưới (phần tô đậm).
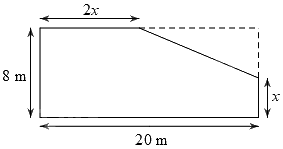
a) Viết biểu thức (thu gọn) T biểu thị theo \(x\) (với \(0 < x < 8\)) diện tích đất bị thu hồi của nhà ông An.
b) Ông An được đền bù số tiền 455 triệu đồng cho diện tích đất bị thu hồi. Tìm giá trị \(x\)(m) biết giá đền bù đất bị thu hồi là 13 triệu đồng\(/{m^2}\).
Phương pháp
a) Phần đất bị cắt đi có hình tam giác vuông.
Sử dụng công thức tính diện tích tam giác để viết biểu diễn diện tích đất bị thu hồi của nhà ông An.
b) Từ T lập phương trình bậc hai một ẩn \(x\) biểu diễn số tiền ông An được đền bù.
Giải phương trình để tìm \(x\).
Lời giải
a) Độ dài hai cạnh góc vuông của phần đất hình tam giác bị cắt đi là: \(20 - 2x\) (m) và \(8 - x\) (m).
Biểu thức T biểu thị theo \(x\) diện tích đất bị thu hồi của nhà ông Thành là
\(T = \frac{1}{2}\left( {20 - 2x} \right)\left( {8 - x} \right) = {x^2} - 18x + 80\left( {{m^2}} \right)\,\) với \(0 < x < 8\).
b) Vì ông Thành được đền bù số tiền 455 triệu đồng cho diện tích đất bị thu hồi nên ta có phương trình:
\(\left( {{x^2} - 18x + 80} \right) \cdot 13 = 455\)
\({x^2} - 18x + 80 = 455:13\)
\({x^2} - 18x + 80 = 35\)
\({x^2} - 18x + 45 = 0\).
Giải phương trình, ta được \(x = 15\) (KTM) hoặc \(x = 3\) (TM).
Vậy \(x = 3\) m.
Câu 5 (1 điểm): Hiện nay, người ta thường dùng chất liệu PVC (polyvinylchloride) để chế tạo vỏ quả bóng cao su dùng trong bóng đá. Một quả bóng hình cầu thường sử dụng từ hai đến bốn lớp vải lót để làm vỏ bóng và một quả bóng đá thường có chu vi đường tròn lớn từ \(58 - 71\)cm tuỳ vào kích thước bóng để phù hợp cho từng lứa tuổi. Bác Minh có một quả bóng đá size số 7 có chu vi \(70\)cm và vỏ quả bóng được tạo thành từ 4 lớp vải lót có độ dày \(2,5\)mm (xem hình ảnh minh hoạ).

a) Tính thể tích không khí tối đa bên trong quả bóng khi quả bóng căng tròn.
b) Sau một thời gian sử dụng, quả bóng không còn chất lượng như ban đầu nên bác Minh cắt quả bóng theo mặt cắt là một đường tròn để tái chế quả bóng thành một chậu cây có dạng như ảnh minh hoạ. Bác Minh dùng dụng cụ xúc đất như hình trên để xúc đất vào quả bóng, biết thể tích dụng cụ xúc đất bằng \(70\% \) thể tích hình trụ có cùng bán kính đáy, chiều cao. Thể tích đất bác Minh cần bỏ vào quả bóng bằng \(\frac{4}{5}\) thể tích quả bóng ban đầu. Hỏi bác Minh cần xúc ít nhất bao nhiêu lần, biết mỗi lần xúc được một thể tích đất bằng thể tích dụng cụ xúc?

(Lấy \(\pi \approx 3,14\), làm tròn kết quả đến hàng phần trăm)
Phương pháp
a) Đổi về cùng đơn vị.
Sử dụng công thức tính chu vi đường tròn \(C = 2\pi R\) để tính bán kính đường tròn lớn.
Từ đó tính được bán kính phần trong của quả bóng.
Tính thể tích phần không khí bên trong khi quả bóng căng tròn bằng công thức tính thể tích hình cầu \(V = \frac{4}{3}\pi {r^3}\).
b) Tính thể tích của phần đất: \({V_{\rm{d}}} = \frac{4}{5}.V\).
Tính thể tích đất thu được sau mỗi lần xúc là: \({V_{{\rm{dc}}}} = 70\% .\pi .{R_{{\rm{dc}}}}^2.{h_{{\rm{dc}}}}\) (dc: dụng cụ)
Tính tỉ số \(\frac{{{V_{\rm{d}}}}}{{{V_{{\rm{dc}}}}}}\). Khi đó ta tính được số lần xúc.
Lời giải
a) Đổi 2,5mm = 0,25cm.
Vì chu vi đường tròn lớn của quả bóng là \(70\)cm nên ta có:
\(2\pi R = 70\) hay \(R = \frac{{70}}{{2\pi }} \approx \frac{{70}}{{2.3,14}} \approx 11,15\) (cm)
Bán kính phần trong của quả bóng là: \(r = R - 0,25 \approx 11,15 - 0,25 = 10,9\) (cm).
Vậy thể tích phần không khí bên trong khi quả bóng căng tròn là:
\(V = \frac{4}{3}\pi {r^3} \approx \frac{4}{3}.3,14.{\left( {10,9} \right)^3} \approx 5421,85\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
b) Thể tích của phần đất là:
\({V_{\rm{d}}} = \frac{4}{5}.V \approx \frac{4}{5}.5421,85 = 4337,48\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Thể tích đất thu được sau mỗi lần xúc là:
\({V_{{\rm{dc}}}} = 70\% .\pi .{R_{{\rm{dc}}}}^2.{h_{{\rm{dc}}}} = 70\% .3,{14.3^2}.15 = 296,73\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Ta có: \(\frac{{{V_{\rm{d}}}}}{{{V_{{\rm{dc}}}}}} = \frac{{4337,48}}{{296,73}} \approx 14,62\)
Do số lần xúc là số tự nhiên nên bác Minh cần xúc ít nhất \(15\) lần để được thể tích đất cần thiết.
Câu 6 (1 điểm): Cách Tết Trung thu 1 tháng, bà Hoa nhập 100 cái bánh dẻo đậu xanh và 150 cái bánh nướng thập cẩm hết 10 230 000 đồng. Thấy bán được, bà Hoa nhập thêm 400 cái bánh dẻo đậu xanh và 200 cái bánh nướng thập cẩm (cùng giá nhập đợt đầu) hết 22 920 000 đồng.
a) Hỏi giá nhập của mỗi chiếc bánh dẻo đậu xanh và bánh nướng thập cẩm là bao nhiêu?
b) Trước Tết Trung thu 3 ngày, bà Hoa đã bán hết bánh nướng thập cẩm nhưng vẫn còn 100 cái bánh dẻo đậu xanh. Để nhanh chóng bán hết số bánh đã nhập về, bà Hoa thực hiện chương trình khuyến mại như sau: mua cái bánh thứ nhất bằng giá niêm yết, cái bánh thứ hai giảm 30% so với giá niêm yết, cái bánh thứ ba trở đi giảm 60% so với giá niêm yết. Bạn Mai đến cửa hàng bà Hoa mua 5 cái bánh dẻo đậu xanh phải trả 145 000 đồng. Hỏi giá niêm yết của mỗi cái bánh dẻo đậu xanh là bao nhiêu?
Phương pháp
a) Gọi giá nhập của mỗi chiếc bánh dẻo đậu xanh và bánh nướng thập cẩm là \(x\) (đồng) và \(y\) (đồng). Điều kiện: \(x,y \in {\mathbb{N}^*}\).
Viết phương trình biểu diễn tiền nhập bánh lần 1 và lần 2 theo \(x,y\).
Giải hệ phương trình vừa lập.
Kiểm tra lại điều kiện và kết luận.
b) Gọi giá niêm yết của mỗi cái bánh dẻo đậu xanh là \(a\) (đồng). Điều kiện : \(a \in {\mathbb{N}^*}\).
Vì bạn Mai đến cửa hàng bà Hoa mua 5 cái bánh dẻo đậu xanh phải trả 145 000 đồng nên ta viết được phương trình.
Giải phương trình.
Kiểm tra lại điều kiện và kết luận.
Lời giải
a) Gọi giá nhập của mỗi chiếc bánh dẻo đậu xanh và bánh nướng thập cẩm là \(x\) (đồng) và \(y\) (đồng). Điều kiện: \(x,y \in {\mathbb{N}^*}\).
Vì bà Hoa nhập 100 cái bánh dẻo đậu xanh và 150 cái bánh nướng thập cẩm hết 10 230 000 đồng nên ta có phương trình:
\(100x + 150y = 10\;230\;000\) (1)
Vì bà Hoa nhập 400 cái bánh dẻo đậu xanh và 200 cái bánh nướng thập cẩm hết 22 920 000 đồng nên ta có phương trình:
\(400x + 200y = 22\;920\;000\) (2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{100x + 150y = 10\;230\;000}\\{400x + 200y = 22\;920\;000.}\end{array}} \right.\)
Giải hệ phương trình ta được \(\left\{ {\begin{array}{*{20}{c}}{x = 34\;800}\\{y = 45\;000}\end{array}} \right.\) (thỏa mãn điều kiện).
Vậy giá nhập của mỗi chiếc bánh dẻo đậu xanh và bánh nướng thập cẩm là 34 800 (đồng) và 45 000 (đồng).
b) Gọi giá niêm yết của mỗi cái bánh dẻo đậu xanh là \(a\) (đồng). Điều kiện : \(a \in {\mathbb{N}^*}\).
Vì bạn Mai đến cửa hàng bà Hoa mua 5 cái bánh dẻo đậu xanh phải trả 145 000 đồng nên ta có phương trình:
\(\begin{array}{l}x + x \cdot \left( {100\% - 30\% } \right) + 3x \cdot \left( {100\% - 60\% } \right) = 145\;000\\x + 0,7x + 1,2x = 145\,000\\2,9x = 145\,000\\x = 50\,000\end{array}\)
Giải phương trình ta được \(x = 50\;000\) (thỏa mãn điều kiện).
Vậy giá niêm yết của mỗi cái bánh dẻo đậu xanh là 50 000 đồng.
Câu 7 (3 điểm): Cho đường tròn tâm \(O\) đường kính \(BC\), điểm \(A\) nằm ngoài đường tròn sao cho \(\widehat {BAC} < 90^\circ \). Gọi \(M,\,N\) là giao điểm của \(AB\) và \(AC\) với đường tròn \(\left( O \right)\) (\(M\) khác \(B\), \(N\) khác \(C\)). Hai đường thẳng \(BN\) và \(CM\) cắt nhau tại \(I\).
a) Chứng minh \(AI \bot BC\) và tứ giác \(MANI\) là tứ giác nội tiếp.
b) Gọi \(D\) là điểm trên cung nhỏ \(MN\) sao cho $\overset\frown{MD}=\overset\frown{ND}$, \(P\) là giao điểm của \(BD\) và \(CM\), \(Q\) là giao điểm của \(CD\) và \(BN\). Chứng minh rằng \(DQ.CD = BD.DP\) và \(\widehat {IPD} = \widehat {IQD}\).
c) Giả sử \(\widehat {BAC} = 60^\circ \) và \(BC = 10\)cm. Tính độ dài \(MN\) và chu vi đường tròn ngoại tiếp \(\Delta MIN\). (lấy \(\pi \approx 3,14\))
Phương pháp
a) Chứng minh \(AI \bot BC\)
Chứng minh \(BN\) và \(CM\) là hai đường cao của tam giác \(ABC\) và cắt nhau tại \(I\) nên \(I\) là trực tâm của tam giác \(ABC\).
Suy ra \(AI \bot BC\).
Chứng minhtứ giác \(MANI\) là tứ giác nội tiếp
Chứng minh \(\Delta AMI\) và \(\Delta ANI\) nội tiếp đường tròn đường kính \(AI\).
Do đó bốn điểm \(A,N,I,M\) thuộc đường tròn đường kính \(AI\) hay tứ giác \(MANI\) là tứ giác nội tiếp.
b) Chứng minh \(DQ.CD = BD.DP\)
Chứng minh \(\Delta DQB\backsim \Delta DPC\) (g-g) suy ra \(DQ.DC = DP.DP\) (đpcm).
Chứng minh \(\widehat {IPD} = \widehat {IQD}\)
Từ \(\Delta DQB\backsim \Delta DPC\) suy ra \(\widehat {IPD} = \widehat {IQD}\).
c) Tính \(MN\)
Chứng minh \(\Delta BAN\backsim \Delta CAM\) (g-g), suy ra \(\frac{AN}{AB}=\frac{AM}{AC}\)
Chứng minh \(\Delta AMN\backsim \Delta ACB\)(c-g-c), suy ra \(\frac{{MN}}{{CB}} = \frac{{AN}}{{AB}} = \cos A\).
Do đó \(MN = CB.\cos A\).
Tính chu vi đường tròn ngoại tiếp tam giác \(MIN\)
Chứng minh \(\widehat {NAI} = \widehat {NBC}\).
Chứng minh \(\Delta ANI\backsim \Delta BNC\) (g-g), suy ra \(\frac{{AI}}{{BC}} = \frac{{NI}}{{NC}} = \cos \widehat {NIC}\).
Chứng minh \(\widehat {NIC} = \widehat {MAN} = 60^\circ \) suy ra \(AI = \cos 60^\circ .BC\).
Đường tròn ngoại tiếp tam giác \(MIN\) có đường kính là \(AI\) nên ta có chu vi của đường tròn đó là:
\(C = \pi .AI\).
Lời giải
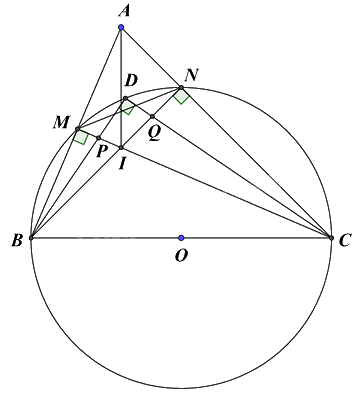
a) Chứng minh \(AI \bot BC\)
Do \(\widehat {BMC}\) và \(\widehat {BNC}\) là hai góc nội tiếp chắn nửa đường tròn nên \(\widehat {BMC} = \widehat {BNC} = 90^\circ \).
Suy ra \(BN\) và \(CM\) là hai đường cao của tam giác \(ABC\).
Mà \(BN\) và \(CM\) cắt nhau tại \(I\) nên \(I\) là trực tâm của tam giác \(ABC\).
Do đó \(AI \bot BC\).
Chứng minhtứ giác \(MANI\) là tứ giác nội tiếp
Vì \(\widehat {AMI} = 90^\circ \) nên \(\Delta AMI\) nội tiếp đường tròn đường kính \(AI\).
Vì \(\widehat {ANI} = 90^\circ \) nên \(\Delta ANI\) nội tiếp đường tròn đường kính \(AI\).
Do đó bốn điểm \(A,N,I,M\) thuộc đường tròn đường kính \(AI\) hay tứ giác \(MANI\) là tứ giác nội tiếp.
b) Chứng minh \(DQ.CD = BD.DP\)
Xét \(\Delta DQB\) và \(\Delta DPC\), ta có:
\(\widehat {BDQ}\) chung
\(\widehat {DBQ} = \widehat {DCQ}\) (là hai góc nội tiếp chắn cung \(DN\), \(DM\) và \(\text{sđ}\overset\frown{DN}=\text{sđ}\overset\frown{DM}\))
Suy ra \(\Delta DQB\backsim \Delta DPC\) (g-g)
Do đó \(\frac{{DQ}}{{DP}} = \frac{{DB}}{{DC}}\) hay \(DQ.DC = DP.DP\) (đpcm).
Chứng minh \(\widehat {IPD} = \widehat {IQD}\)
Vì \(\Delta DQB\backsim \Delta DPC\) nên \(\widehat {IQD} = \widehat {CPD}\) hay \(\widehat {IPD} = \widehat {IQD}\).
c) Tính \(MN\)
Xét \(\Delta BAN\) và \(\Delta CAM\), ta có:
\(\widehat {BAN}\) chung
\(\widehat {BNA} = \widehat {CMA} = {90^0}\)
Suy ra \(\Delta BAN\backsim \Delta CAM\) (g-g), suy ra \(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\)
Xét \(\Delta AMN\) và \(\Delta ACB\), ta có
\(\widehat {BAC}\) chung
\(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\) (cmt)
Suy ra \(\Delta AMN\backsim \Delta ACB\)(c-g-c), suy ra \(\frac{{MN}}{{CB}} = \frac{{AN}}{{AB}} = \cos A = \cos 60^\circ = \frac{1}{2}\).
Do đó, \(MN = CB.\frac{1}{2} = 10.\frac{1}{2} = 5\left( {{\rm{cm}}} \right)\).
Tính chu vi đường tròn ngoại tiếp tam giác \(MIN\)
Ta có: \(\widehat {NAI} = \widehat {NMI}\) (tứ giác \(MANI\) nội tiếp và \(\widehat {NAI}\) và \(\widehat {NMI}\) là góc nội tiếp chắn \(\overset\frown{NI}\))
Và \(\widehat {NMI} = \widehat {NBC}\) (góc nội tiếp chắn \(\overset\frown{NC}\)).
Suy ra \(\widehat {NAI} = \widehat {NBC}\).
Xét \(\Delta ANI\) và \(\Delta BNC\) có:
\(\widehat {ANI} = \widehat {BNC} = 90^\circ \)
\(\widehat {NAI} = \widehat {NBC}\) (cmt)
Suy ra \(\Delta ANI\backsim \Delta BNC\) (g-g), suy ra \(\frac{{AI}}{{BC}} = \frac{{NI}}{{NC}} = \cos \widehat {NIC}\).
Mà \(\widehat {NIC} = \widehat {MAN} = 60^\circ \) (vì \(\widehat {NIC}\) và \(\widehat {MAN}\) cùng bù với \(\widehat {MIN}\))
Suy ra \(\frac{{AI}}{{BC}} = \cos {60^0} = \frac{1}{2}\), do đó \(AI = \frac{1}{2}.BC = \frac{1}{2}.10 = 5\left( {{\rm{cm}}} \right)\).
Mà đường tròn ngoại tiếp tam giác \(MIN\) có đường kính là \(AI\) nên ta có chu vi của đường tròn đó là:
\(C = \pi .AI = 3,14.5 \approx 15,7\left( {{\rm{cm}}} \right)\).
Câu 1 (1,5 điểm): Cho hàm số \(\left( P \right):y = - \frac{{{x^2}}}{4}\).
a) Vẽ đồ thị \(\left( P \right)\) của hàm số trên.
b) Tìm trên \(\left( P \right)\) những điểm có tung độ gấp \(3\) lần hoành độ.
Phương pháp
a) Lập bảng giá trị, vẽ đồ thị hàm số trên hệ trục tọa độ.
b) Gọi điểm thuộc \(\left( P \right)\) có tung độ gấp \(3\) lần hoành độ có toạ độ là \(\left( {{x_0};3{x_0}} \right)\).
Thay \({y_0} = 3{x_0}\) vào hàm số và giải phương trình đưa về phương trình tích.
Lời giải
a) Ta có bảng giá trị:

Đồ thị \(\left( P \right)\) của hàm số là đường cong parabol đi qua các điểm
\(O\,\left( {0;0} \right);A\left( { - 2; - 1} \right);B\left( { - 1; - \frac{1}{4}} \right);\,\,C\left( {1; - \frac{1}{4}} \right);\,\,D\left( {2; - 1} \right)\)
Ta vẽ được đồ thị hàm số \(y = - \frac{{{x^2}}}{4}\) như sau:
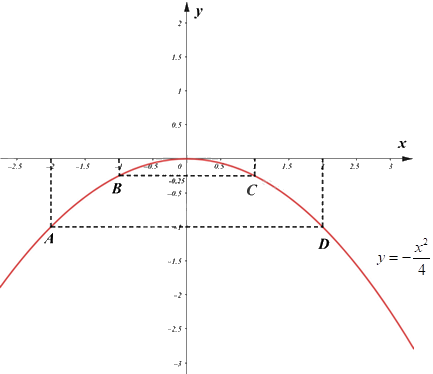
b) Gọi điểm thuộc \(\left( P \right)\) có tung độ gấp \(3\) lần hoành độ có toạ độ là \(\left( {{x_0};3{x_0}} \right)\).
Vì điểm nằm trên đồ thị của hàm số \(y = - \frac{{{x^2}}}{4}\) nên ta có:
\(\begin{array}{l}3{x_0} = - \frac{{x_0^2}}{4}\\12{x_0} = - x_0^2\\x_0^2 + 12{x_0} = 0\\{x_0}\left( {{x_0} + 12} \right) = 0\end{array}\)
Suy ra \({x_0} = 0\) hoặc \({x_0} = - 12\).
Vậy những điểm có tung độ gấp \(3\) lần hoành độ trên \(\left( P \right)\) là \(\left( {0;0} \right)\) và \(\left( { - 12; - 36} \right)\).
Câu 2 (1 điểm): Cho phương trình \(4{x^2} + 4x - 3 = 0\)
a) Không giải phương trình, chứng minh phương trình luôn có hai nghiệm phân biệt.
b) Tính giá trị biểu thức \(A = {x_1}\left( {4 + \frac{1}{3}{x_2}} \right) + 4{x_2}\).
Phương pháp
a) Kiểm tra nghiệm của phương trình theo \(a.c\).
b) Áp dụng định lí Viète và biến đổi.
Định lí Viète: \({x_1} + {x_2} = \frac{{ - b}}{a};{x_1}{x_2} = \frac{c}{a}\)
Lời giải
a) Phương trình \(4{x^2} + 4x - 3 = 0\) có:
\(a.c = 4.\left( { - 3} \right) = - 12 < 0\) nên phương trình có hai nghiệm phân biệt \({x_1},{x_2}\).
b) Áp dụng định lí Viète, ta có:
\(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - 4}}{4} = - 1}\\{{x_1}{x_2} = \frac{{ - 3}}{4}}\end{array}} \right.\)
Ta có: \(A = {x_1}\left( {4 + \frac{1}{3}{x_2}} \right) + 4{x_2}\)
\(\begin{array}{l} = 4{x_1} + \frac{1}{3}{x_1}{x_2} + 4{x_2}\\ = 4({x_1} + {x_2}) + \frac{1}{3}{x_1}{x_2}\\ = 4.( - 1) + \frac{1}{3}.\left( { - \frac{3}{4}} \right)\\ = - \frac{{17}}{4}\end{array}\)
Vậy \(A = - \frac{{17}}{4}\).
Câu 3 (1,5 điểm): Biểu đồ cột kép dưới đây biểu diễn lượng mưa trung bình (đơn vị: mm) của các tháng trong một năm ở Hà Nội và Thành phố Hồ Chí Minh.
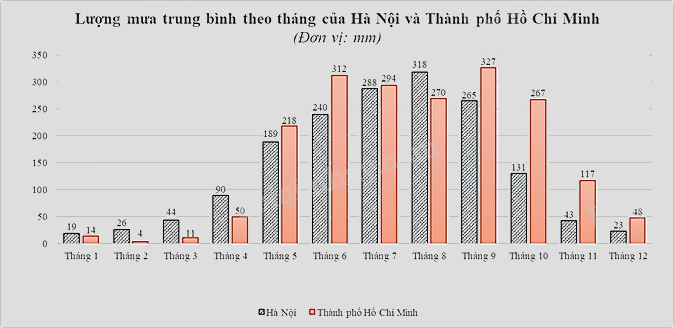
a) Tính lượng mưa chênh lệch trung bình ở hai địa điểm Hà Nội và Thành phố Hồ Chí Minh.
b) Chọn ngẫu nhiên một tháng trong năm, tính xác suất của các biến cố sau:
\(P\): “Lượng mưa trung bình của Thành phố Hồ Chí Minh lớn hơn \(200\)mm”
\(Q\): “Lượng mưa chênh lệch của Hà Nội và Thành phố Hồ Chí Minh không vượt quá \(40\)mm”
Phương pháp
a) Quan sát biểu đồ, xác định lượng mưa chênh lệch ở hai địa điểm Hà Nội và Thành phố Hồ Chí Minh theo từng tháng = giá trị lớn hơn – giá trị nhỏ hơn.
Lượng mưa chênh lệch trung bình = tổng lượng lượng mưa chênh lệch của 12 tháng : 12 tháng.
b) Xác định số phần tử của không gian mẫu, biến cố P và Q, từ đó tính xác suất của biến cố = số phần tử của biến cố : số phần tử của không gian mẫu.
Lời giải
a)Lượng mưa chênh lệch ở hai địa điểm Hà Nội và Thành phố Hồ Chí Minh theo từng tháng là:
Tháng 1: \(19 - 14 = 5\)
Tháng 2: \(26 - 4 = 22\)
Tháng 3: \(44 - 11 = 33\)
Tháng 4: \(90 - 50 = 40\)
Tháng 5: \(218 - 189 = 29\)
Tháng 6: \(312 - 240 = 72\)
Tháng 7: \(294 - 288 = 6\)
Tháng 8: \(318 - 270 = 48\)
Tháng 9: \(327 - 265 = 62\)
Tháng 10: \(267 - 131 = 136\)
Tháng 11: \(117 - 43 = 74\)
Tháng 12: \(48 - 23 = 25\)
Lượng mưa chênh lệch trung bình là:
\(\frac{{5 + 22 + 33 + 40 + 29 + 72 + 6 + 48 + 62 + 136 + 74 + 25}}{{12}} = 46\)(mm)
b) Không gian mẫu có số phần tử là 12.
Xét biến cố \(P\): “Lượng mưa trung bình của Thành phố Hồ Chí Minh lớn hơn \(200\)mm”.
Số tháng được chọn có lượng mưa trung bình của Thành phố Hồ Chí Minh lớn hơn \(200\)mm là \(6\) tháng: tháng 5, 6, 7, 8, 9, 10.
Suy ra số phần tử của biến cố \(P\) là 6.
Vậy xác suất của biến cố \(P\) là: \(p\left( P \right)=\frac{6}{12}=\frac{1}{2}\).
Xét biến cố \(Q\): “Lượng mưa chênh lệch của Hà Nội và Thành phố Hồ Chí Minh không vượt quá \(40\)mm”.
Số tháng được chọn có lượng mưa chênh lệch của Hà Nội và Thành phố Hồ Chí Minh không vượt quá \(40\)mm là \(7\) tháng: tháng 1; 2; 3; 4; 5; 7; 12.
Suy ra số phần tử của biến cố \(Q\) là \(7\).
Vậy xác suất của biến cố \(Q\) là: \(p\left( Q \right)=\frac{7}{12}\).
Câu 4 (1 điểm): Ông An có một mảnh đất hình chữ nhật có chiều rộng là 8 m và chiều dài là 20 m. Nhà nước làm một con đường đi ngang qua mảnh đất của ông An và thu hồi một phần đất của ông An (phần hình tam giác). Phần đất không bị thu hồi có kích thước như hình vẽ dưới (phần tô đậm).
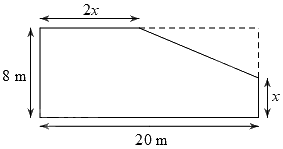
a) Viết biểu thức (thu gọn) T biểu thị theo \(x\) (với \(0 < x < 8\)) diện tích đất bị thu hồi của nhà ông An.
b) Ông An được đền bù số tiền 455 triệu đồng cho diện tích đất bị thu hồi. Tìm giá trị \(x\)(m) biết giá đền bù đất bị thu hồi là 13 triệu đồng\(/{m^2}\).
Phương pháp
a) Phần đất bị cắt đi có hình tam giác vuông.
Sử dụng công thức tính diện tích tam giác để viết biểu diễn diện tích đất bị thu hồi của nhà ông An.
b) Từ T lập phương trình bậc hai một ẩn \(x\) biểu diễn số tiền ông An được đền bù.
Giải phương trình để tìm \(x\).
Lời giải
a) Độ dài hai cạnh góc vuông của phần đất hình tam giác bị cắt đi là: \(20 - 2x\) (m) và \(8 - x\) (m).
Biểu thức T biểu thị theo \(x\) diện tích đất bị thu hồi của nhà ông Thành là
\(T = \frac{1}{2}\left( {20 - 2x} \right)\left( {8 - x} \right) = {x^2} - 18x + 80\left( {{m^2}} \right)\,\) với \(0 < x < 8\).
b) Vì ông Thành được đền bù số tiền 455 triệu đồng cho diện tích đất bị thu hồi nên ta có phương trình:
\(\left( {{x^2} - 18x + 80} \right) \cdot 13 = 455\)
\({x^2} - 18x + 80 = 455:13\)
\({x^2} - 18x + 80 = 35\)
\({x^2} - 18x + 45 = 0\).
Giải phương trình, ta được \(x = 15\) (KTM) hoặc \(x = 3\) (TM).
Vậy \(x = 3\) m.
Câu 5 (1 điểm): Hiện nay, người ta thường dùng chất liệu PVC (polyvinylchloride) để chế tạo vỏ quả bóng cao su dùng trong bóng đá. Một quả bóng hình cầu thường sử dụng từ hai đến bốn lớp vải lót để làm vỏ bóng và một quả bóng đá thường có chu vi đường tròn lớn từ \(58 - 71\)cm tuỳ vào kích thước bóng để phù hợp cho từng lứa tuổi. Bác Minh có một quả bóng đá size số 7 có chu vi \(70\)cm và vỏ quả bóng được tạo thành từ 4 lớp vải lót có độ dày \(2,5\)mm (xem hình ảnh minh hoạ).

a) Tính thể tích không khí tối đa bên trong quả bóng khi quả bóng căng tròn.
b) Sau một thời gian sử dụng, quả bóng không còn chất lượng như ban đầu nên bác Minh cắt quả bóng theo mặt cắt là một đường tròn để tái chế quả bóng thành một chậu cây có dạng như ảnh minh hoạ. Bác Minh dùng dụng cụ xúc đất như hình trên để xúc đất vào quả bóng, biết thể tích dụng cụ xúc đất bằng \(70\% \) thể tích hình trụ có cùng bán kính đáy, chiều cao. Thể tích đất bác Minh cần bỏ vào quả bóng bằng \(\frac{4}{5}\) thể tích quả bóng ban đầu. Hỏi bác Minh cần xúc ít nhất bao nhiêu lần, biết mỗi lần xúc được một thể tích đất bằng thể tích dụng cụ xúc?

(Lấy \(\pi \approx 3,14\), làm tròn kết quả đến hàng phần trăm)
Phương pháp
a) Đổi về cùng đơn vị.
Sử dụng công thức tính chu vi đường tròn \(C = 2\pi R\) để tính bán kính đường tròn lớn.
Từ đó tính được bán kính phần trong của quả bóng.
Tính thể tích phần không khí bên trong khi quả bóng căng tròn bằng công thức tính thể tích hình cầu \(V = \frac{4}{3}\pi {r^3}\).
b) Tính thể tích của phần đất: \({V_{\rm{d}}} = \frac{4}{5}.V\).
Tính thể tích đất thu được sau mỗi lần xúc là: \({V_{{\rm{dc}}}} = 70\% .\pi .{R_{{\rm{dc}}}}^2.{h_{{\rm{dc}}}}\) (dc: dụng cụ)
Tính tỉ số \(\frac{{{V_{\rm{d}}}}}{{{V_{{\rm{dc}}}}}}\). Khi đó ta tính được số lần xúc.
Lời giải
a) Đổi 2,5mm = 0,25cm.
Vì chu vi đường tròn lớn của quả bóng là \(70\)cm nên ta có:
\(2\pi R = 70\) hay \(R = \frac{{70}}{{2\pi }} \approx \frac{{70}}{{2.3,14}} \approx 11,15\) (cm)
Bán kính phần trong của quả bóng là: \(r = R - 0,25 \approx 11,15 - 0,25 = 10,9\) (cm).
Vậy thể tích phần không khí bên trong khi quả bóng căng tròn là:
\(V = \frac{4}{3}\pi {r^3} \approx \frac{4}{3}.3,14.{\left( {10,9} \right)^3} \approx 5421,85\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
b) Thể tích của phần đất là:
\({V_{\rm{d}}} = \frac{4}{5}.V \approx \frac{4}{5}.5421,85 = 4337,48\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Thể tích đất thu được sau mỗi lần xúc là:
\({V_{{\rm{dc}}}} = 70\% .\pi .{R_{{\rm{dc}}}}^2.{h_{{\rm{dc}}}} = 70\% .3,{14.3^2}.15 = 296,73\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)
Ta có: \(\frac{{{V_{\rm{d}}}}}{{{V_{{\rm{dc}}}}}} = \frac{{4337,48}}{{296,73}} \approx 14,62\)
Do số lần xúc là số tự nhiên nên bác Minh cần xúc ít nhất \(15\) lần để được thể tích đất cần thiết.
Câu 6 (1 điểm): Cách Tết Trung thu 1 tháng, bà Hoa nhập 100 cái bánh dẻo đậu xanh và 150 cái bánh nướng thập cẩm hết 10 230 000 đồng. Thấy bán được, bà Hoa nhập thêm 400 cái bánh dẻo đậu xanh và 200 cái bánh nướng thập cẩm (cùng giá nhập đợt đầu) hết 22 920 000 đồng.
a) Hỏi giá nhập của mỗi chiếc bánh dẻo đậu xanh và bánh nướng thập cẩm là bao nhiêu?
b) Trước Tết Trung thu 3 ngày, bà Hoa đã bán hết bánh nướng thập cẩm nhưng vẫn còn 100 cái bánh dẻo đậu xanh. Để nhanh chóng bán hết số bánh đã nhập về, bà Hoa thực hiện chương trình khuyến mại như sau: mua cái bánh thứ nhất bằng giá niêm yết, cái bánh thứ hai giảm 30% so với giá niêm yết, cái bánh thứ ba trở đi giảm 60% so với giá niêm yết. Bạn Mai đến cửa hàng bà Hoa mua 5 cái bánh dẻo đậu xanh phải trả 145 000 đồng. Hỏi giá niêm yết của mỗi cái bánh dẻo đậu xanh là bao nhiêu?
Phương pháp
a) Gọi giá nhập của mỗi chiếc bánh dẻo đậu xanh và bánh nướng thập cẩm là \(x\) (đồng) và \(y\) (đồng). Điều kiện: \(x,y \in {\mathbb{N}^*}\).
Viết phương trình biểu diễn tiền nhập bánh lần 1 và lần 2 theo \(x,y\).
Giải hệ phương trình vừa lập.
Kiểm tra lại điều kiện và kết luận.
b) Gọi giá niêm yết của mỗi cái bánh dẻo đậu xanh là \(a\) (đồng). Điều kiện : \(a \in {\mathbb{N}^*}\).
Vì bạn Mai đến cửa hàng bà Hoa mua 5 cái bánh dẻo đậu xanh phải trả 145 000 đồng nên ta viết được phương trình.
Giải phương trình.
Kiểm tra lại điều kiện và kết luận.
Lời giải
a) Gọi giá nhập của mỗi chiếc bánh dẻo đậu xanh và bánh nướng thập cẩm là \(x\) (đồng) và \(y\) (đồng). Điều kiện: \(x,y \in {\mathbb{N}^*}\).
Vì bà Hoa nhập 100 cái bánh dẻo đậu xanh và 150 cái bánh nướng thập cẩm hết 10 230 000 đồng nên ta có phương trình:
\(100x + 150y = 10\;230\;000\) (1)
Vì bà Hoa nhập 400 cái bánh dẻo đậu xanh và 200 cái bánh nướng thập cẩm hết 22 920 000 đồng nên ta có phương trình:
\(400x + 200y = 22\;920\;000\) (2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{100x + 150y = 10\;230\;000}\\{400x + 200y = 22\;920\;000.}\end{array}} \right.\)
Giải hệ phương trình ta được \(\left\{ {\begin{array}{*{20}{c}}{x = 34\;800}\\{y = 45\;000}\end{array}} \right.\) (thỏa mãn điều kiện).
Vậy giá nhập của mỗi chiếc bánh dẻo đậu xanh và bánh nướng thập cẩm là 34 800 (đồng) và 45 000 (đồng).
b) Gọi giá niêm yết của mỗi cái bánh dẻo đậu xanh là \(a\) (đồng). Điều kiện : \(a \in {\mathbb{N}^*}\).
Vì bạn Mai đến cửa hàng bà Hoa mua 5 cái bánh dẻo đậu xanh phải trả 145 000 đồng nên ta có phương trình:
\(\begin{array}{l}x + x \cdot \left( {100\% - 30\% } \right) + 3x \cdot \left( {100\% - 60\% } \right) = 145\;000\\x + 0,7x + 1,2x = 145\,000\\2,9x = 145\,000\\x = 50\,000\end{array}\)
Giải phương trình ta được \(x = 50\;000\) (thỏa mãn điều kiện).
Vậy giá niêm yết của mỗi cái bánh dẻo đậu xanh là 50 000 đồng.
Câu 7 (3 điểm): Cho đường tròn tâm \(O\) đường kính \(BC\), điểm \(A\) nằm ngoài đường tròn sao cho \(\widehat {BAC} < 90^\circ \). Gọi \(M,\,N\) là giao điểm của \(AB\) và \(AC\) với đường tròn \(\left( O \right)\) (\(M\) khác \(B\), \(N\) khác \(C\)). Hai đường thẳng \(BN\) và \(CM\) cắt nhau tại \(I\).
a) Chứng minh \(AI \bot BC\) và tứ giác \(MANI\) là tứ giác nội tiếp.
b) Gọi \(D\) là điểm trên cung nhỏ \(MN\) sao cho $\overset\frown{MD}=\overset\frown{ND}$, \(P\) là giao điểm của \(BD\) và \(CM\), \(Q\) là giao điểm của \(CD\) và \(BN\). Chứng minh rằng \(DQ.CD = BD.DP\) và \(\widehat {IPD} = \widehat {IQD}\).
c) Giả sử \(\widehat {BAC} = 60^\circ \) và \(BC = 10\)cm. Tính độ dài \(MN\) và chu vi đường tròn ngoại tiếp \(\Delta MIN\). (lấy \(\pi \approx 3,14\))
Phương pháp
a) Chứng minh \(AI \bot BC\)
Chứng minh \(BN\) và \(CM\) là hai đường cao của tam giác \(ABC\) và cắt nhau tại \(I\) nên \(I\) là trực tâm của tam giác \(ABC\).
Suy ra \(AI \bot BC\).
Chứng minhtứ giác \(MANI\) là tứ giác nội tiếp
Chứng minh \(\Delta AMI\) và \(\Delta ANI\) nội tiếp đường tròn đường kính \(AI\).
Do đó bốn điểm \(A,N,I,M\) thuộc đường tròn đường kính \(AI\) hay tứ giác \(MANI\) là tứ giác nội tiếp.
b) Chứng minh \(DQ.CD = BD.DP\)
Chứng minh \(\Delta DQB\backsim \Delta DPC\) (g-g) suy ra \(DQ.DC = DP.DP\) (đpcm).
Chứng minh \(\widehat {IPD} = \widehat {IQD}\)
Từ \(\Delta DQB\backsim \Delta DPC\) suy ra \(\widehat {IPD} = \widehat {IQD}\).
c) Tính \(MN\)
Chứng minh \(\Delta BAN\backsim \Delta CAM\) (g-g), suy ra \(\frac{AN}{AB}=\frac{AM}{AC}\)
Chứng minh \(\Delta AMN\backsim \Delta ACB\)(c-g-c), suy ra \(\frac{{MN}}{{CB}} = \frac{{AN}}{{AB}} = \cos A\).
Do đó \(MN = CB.\cos A\).
Tính chu vi đường tròn ngoại tiếp tam giác \(MIN\)
Chứng minh \(\widehat {NAI} = \widehat {NBC}\).
Chứng minh \(\Delta ANI\backsim \Delta BNC\) (g-g), suy ra \(\frac{{AI}}{{BC}} = \frac{{NI}}{{NC}} = \cos \widehat {NIC}\).
Chứng minh \(\widehat {NIC} = \widehat {MAN} = 60^\circ \) suy ra \(AI = \cos 60^\circ .BC\).
Đường tròn ngoại tiếp tam giác \(MIN\) có đường kính là \(AI\) nên ta có chu vi của đường tròn đó là:
\(C = \pi .AI\).
Lời giải
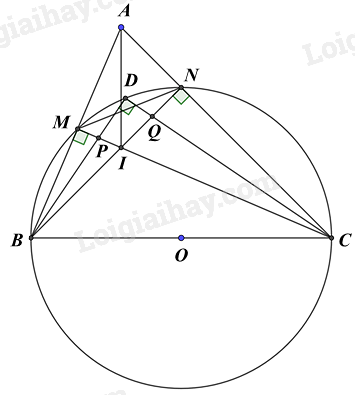
a) Chứng minh \(AI \bot BC\)
Do \(\widehat {BMC}\) và \(\widehat {BNC}\) là hai góc nội tiếp chắn nửa đường tròn nên \(\widehat {BMC} = \widehat {BNC} = 90^\circ \).
Suy ra \(BN\) và \(CM\) là hai đường cao của tam giác \(ABC\).
Mà \(BN\) và \(CM\) cắt nhau tại \(I\) nên \(I\) là trực tâm của tam giác \(ABC\).
Do đó \(AI \bot BC\).
Chứng minhtứ giác \(MANI\) là tứ giác nội tiếp
Vì \(\widehat {AMI} = 90^\circ \) nên \(\Delta AMI\) nội tiếp đường tròn đường kính \(AI\).
Vì \(\widehat {ANI} = 90^\circ \) nên \(\Delta ANI\) nội tiếp đường tròn đường kính \(AI\).
Do đó bốn điểm \(A,N,I,M\) thuộc đường tròn đường kính \(AI\) hay tứ giác \(MANI\) là tứ giác nội tiếp.
b) Chứng minh \(DQ.CD = BD.DP\)
Xét \(\Delta DQB\) và \(\Delta DPC\), ta có:
\(\widehat {BDQ}\) chung
\(\widehat {DBQ} = \widehat {DCQ}\) (là hai góc nội tiếp chắn cung \(DN\), \(DM\) và \(\text{sđ}\overset\frown{DN}=\text{sđ}\overset\frown{DM}\))
Suy ra \(\Delta DQB\backsim \Delta DPC\) (g-g)
Do đó \(\frac{{DQ}}{{DP}} = \frac{{DB}}{{DC}}\) hay \(DQ.DC = DP.DP\) (đpcm).
Chứng minh \(\widehat {IPD} = \widehat {IQD}\)
Vì \(\Delta DQB\backsim \Delta DPC\) nên \(\widehat {IQD} = \widehat {CPD}\) hay \(\widehat {IPD} = \widehat {IQD}\).
c) Tính \(MN\)
Xét \(\Delta BAN\) và \(\Delta CAM\), ta có:
\(\widehat {BAN}\) chung
\(\widehat {BNA} = \widehat {CMA} = {90^0}\)
Suy ra \(\Delta BAN\backsim \Delta CAM\) (g-g), suy ra \(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\)
Xét \(\Delta AMN\) và \(\Delta ACB\), ta có
\(\widehat {BAC}\) chung
\(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\) (cmt)
Suy ra \(\Delta AMN\backsim \Delta ACB\)(c-g-c), suy ra \(\frac{{MN}}{{CB}} = \frac{{AN}}{{AB}} = \cos A = \cos 60^\circ = \frac{1}{2}\).
Do đó, \(MN = CB.\frac{1}{2} = 10.\frac{1}{2} = 5\left( {{\rm{cm}}} \right)\).
Tính chu vi đường tròn ngoại tiếp tam giác \(MIN\)
Ta có: \(\widehat {NAI} = \widehat {NMI}\) (tứ giác \(MANI\) nội tiếp và \(\widehat {NAI}\) và \(\widehat {NMI}\) là góc nội tiếp chắn \(\overset\frown{NI}\))
Và \(\widehat {NMI} = \widehat {NBC}\) (góc nội tiếp chắn \(\overset\frown{NC}\)).
Suy ra \(\widehat {NAI} = \widehat {NBC}\).
Xét \(\Delta ANI\) và \(\Delta BNC\) có:
\(\widehat {ANI} = \widehat {BNC} = 90^\circ \)
\(\widehat {NAI} = \widehat {NBC}\) (cmt)
Suy ra \(\Delta ANI\backsim \Delta BNC\) (g-g), suy ra \(\frac{{AI}}{{BC}} = \frac{{NI}}{{NC}} = \cos \widehat {NIC}\).
Mà \(\widehat {NIC} = \widehat {MAN} = 60^\circ \) (vì \(\widehat {NIC}\) và \(\widehat {MAN}\) cùng bù với \(\widehat {MIN}\))
Suy ra \(\frac{{AI}}{{BC}} = \cos {60^0} = \frac{1}{2}\), do đó \(AI = \frac{1}{2}.BC = \frac{1}{2}.10 = 5\left( {{\rm{cm}}} \right)\).
Mà đường tròn ngoại tiếp tam giác \(MIN\) có đường kính là \(AI\) nên ta có chu vi của đường tròn đó là:
\(C = \pi .AI = 3,14.5 \approx 15,7\left( {{\rm{cm}}} \right)\).
Kỳ thi tuyển sinh vào lớp 10 tại TP. Hồ Chí Minh là một bước ngoặt quan trọng trong sự nghiệp học tập của mỗi học sinh. Để đạt được kết quả tốt nhất, việc luyện tập với các đề tham khảo là vô cùng cần thiết. Đề tham khảo thi vào 10 môn Toán TP Hồ Chí Minh năm 2025 - Đề số 2 của giaitoan.edu.vn được thiết kế để giúp học sinh làm quen với cấu trúc đề thi, rèn luyện kỹ năng giải toán và tự tin hơn trong kỳ thi chính thức.
Đề thi này bao gồm hai phần chính: trắc nghiệm và tự luận. Phần trắc nghiệm chiếm khoảng 40% tổng số điểm, tập trung vào các kiến thức cơ bản và khả năng vận dụng nhanh của học sinh. Phần tự luận chiếm 60% tổng số điểm, đòi hỏi học sinh phải có khả năng phân tích, suy luận và trình bày lời giải một cách logic và chính xác.
Nội dung đề thi bao gồm các chủ đề chính sau:
Sau mỗi câu hỏi, chúng tôi cung cấp hướng dẫn giải chi tiết, giúp học sinh hiểu rõ phương pháp giải và tránh những sai lầm thường gặp. Các lời giải được trình bày một cách dễ hiểu, dễ theo dõi, phù hợp với trình độ của học sinh lớp 9.
Ngoài đề tham khảo số 2 này, giaitoan.edu.vn còn cung cấp nhiều đề tham khảo khác với các mức độ khó khác nhau. Hãy luyện tập với nhiều đề khác nhau để nâng cao khả năng giải toán và chuẩn bị tốt nhất cho kỳ thi tuyển sinh vào 10.
| Đề Số | Mức Độ Khó | Thời Gian Giải |
|---|---|---|
| Đề 1 | Dễ | 60 phút |
| Đề 2 | Trung Bình | 90 phút |
| Đề 3 | Khó | 120 phút |
Chúc các em học sinh ôn tập tốt và đạt kết quả cao trong kỳ thi tuyển sinh vào lớp 10!