Chào mừng các em học sinh đến với Đề số 5 - Đề thi vào lớp 10 môn Toán tại giaitoan.edu.vn. Đây là một trong những đề thi thử quan trọng giúp các em làm quen với cấu trúc đề thi tuyển sinh vào lớp 10 và rèn luyện kỹ năng giải toán.
Đề thi này được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm, bám sát chương trình học và có độ khó tương đương với các đề thi chính thức.
Cùng giaitoan.edu.vn chinh phục kỳ thi vào lớp 10 môn Toán nhé!
Đề thi vào lớp 10 môn Toán - Đề số 5 có đáp án và lời giải chi tiết
Đề bài
Câu 1. (2,5 điểm)
1. Thực hiện phép tính \(\dfrac{{\sqrt {27} }}{{\sqrt 3 }}\)
2. Rút gọn biểu thức \(P = \left( {\dfrac{{\sqrt x }}{{3 + \sqrt x }} + \dfrac{{9 + x}}{{9 - x}}} \right).\left( {3\sqrt x - x} \right)\) với \(x \ge 0\) và \(x \ne 9\)
3. Xác định các hệ số a, b để đồ thị hàm số \(y = ax + b\) đi qua hai điểm \(A\left( {2; - 2} \right)\) và \(B\left( { - 3;2} \right)\)
Câu 2. (1.5 điểm)
1. Giải phương trình \({x^2} - 4x + 4 = 0\)
2. Tìm giá trị của m để phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3 = 0\) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(\left| {{x_1}} \right| + \left| {{x_2}} \right| = 10.\)
Câu 3. (2 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một xe ô tô đi từ A đến B theo đường quốc lộ cũ dài 156 km với vận tốc không đổi. Khi từ B về A, xe đi đường cao tốc mới nên quãng đường giảm được 36 km so với lúc đi và vận tốc tăng so với lúc đi là 32 km/h. Tính vận tốc ô tô khi đi từ A đến B, biết thời gian đi nhiều hơn thời gian về là 1 giờ 45 phút.
Câu 4. (3,5 điểm)
Cho đường tròn tâm O, đường kính AB = 2R. Trên đường tròn (O) lấy điểm C bất kì (C không trùng với A và B). Tiếp tuyến của đường tròn (O) tại A cắt tia BC ở điểm D. Gọi H là hình chiếu của A trên đường thẳng DO. Tia AH cắt đường tròn (O) tại điểm F (không trùng với A). Chứng minh
a) \(D{A^2} = DC.DB\)
b) Tứ giác AHCD nội tiếp.
c) \(CH \bot CF\)
d) \(\dfrac{{BH.BC}}{{BF}} = 2R\)
Câu 5 (0,5 điểm)
Cho x, y là các số thực dương thỏa mãn \(xy + 1 \le x\). Tìm giá trị nhỏ nhất của biểu thức \(Q = \dfrac{{x + y}}{{\sqrt {3{x^2} - xy + {y^2}} }}\)
Lời giải chi tiết
Câu 1.
1. Thực hiện phép tính \(\dfrac{{\sqrt {27} }}{{\sqrt 3 }}\)
\(\dfrac{{\sqrt {27} }}{{\sqrt 3 }} = \sqrt {\dfrac{{27}}{3}} = \sqrt 9 = 3.\)
2. Rút gọn biểu thức \(P = \left( {\dfrac{{\sqrt x }}{{3 + \sqrt x }} + \dfrac{{9 + x}}{{9 - x}}} \right).\left( {3\sqrt x - x} \right)\) với \(x \ge 0\) và \(x \ne 9\)
Điều kiện: \(x \ge 0,\;\;x \ne 9.\)
\(\begin{array}{l}P = \left( {\dfrac{{\sqrt x }}{{3 + \sqrt x }} + \dfrac{{9 + x}}{{9 - x}}} \right).\left( {3\sqrt x - x} \right)\\\;\;\; = \left( {\dfrac{{\sqrt x .\left( {3 - \sqrt x } \right)}}{{\left( {3 - \sqrt x } \right)\left( {3 + \sqrt x } \right)}} + \dfrac{{9 + x}}{{\left( {3 - \sqrt x } \right)\left( {3 + \sqrt x } \right)}}} \right).\left( {3\sqrt x - x} \right)\\\;\;\; = \dfrac{{9 + 3\sqrt x }}{{\left( {3 - \sqrt x } \right)\left( {3 + \sqrt x } \right)}}.\left( {3\sqrt x - x} \right)\\\;\;\; = \dfrac{{3\left( {3 + \sqrt x } \right)}}{{3 + \sqrt x }}.\sqrt x \\\;\;\; = 3\sqrt x .\end{array}\)
3. Xác định các hệ số a, b để đồ thị hàm số \(y = ax + b\) đi qua hai điểm \(A\left( {2; - 2} \right)\) và \(B\left( { - 3;2} \right)\)
Đồ thị hàm số \(y = ax + b\) đi qua hai điểm \(A\left( {2; - 2} \right)\) và \(B\left( { - 3;2} \right)\) nên ta có hệ phương trình:
\(\left\{ \begin{array}{l}2a + b = - 2\\ - 3a + b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5a = - 4\\b = 2 + 3a\end{array} \right. \)
\(\Leftrightarrow \left\{ \begin{array}{l}a = - \dfrac{4}{5}\\b = - \dfrac{2}{5}\end{array} \right.\)
Vậy ta có \(a = - \dfrac{4}{5};\;\;b = - \dfrac{2}{5}.\)
Câu 2.
1. Giải phương trình \({x^2} - 4x + 4 = 0\)
\({x^2} - 4x + 4 = 0\)
\(\Leftrightarrow {\left( {x - 2} \right)^2} = 0 \Leftrightarrow x = 2\)
Vậy tập nghiệm của phương trình là \(S=\{2\}\)
2. Tìm giá trị của m để phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} + 3 = 0\) (*) có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(\left| {{x_1}} \right| + \left| {{x_2}} \right| = 10\)
+) Phương trình có hai nghiệm \({x_1},{x_2}\) khi và chỉ khi \(\Delta ' \ge 0 \Leftrightarrow {\left( {m + 1} \right)^2} - {m^2} - 3 \ge 0\)
\(\Leftrightarrow {m^2} + 2m + 1 - {m^2} - 3 \ge 0 \)
\(\Leftrightarrow 2m \ge 2 \Leftrightarrow m \ge 1.\)
Áp dụng hệ thức Vi-et cho phương trình (*) ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 1} \right)\,\,\left( 2 \right)\\{x_1}{x_2} = {m^2} + 3\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\end{array} \right.\)
Từ đề bài ta có: \(\left| {{x_1}} \right| + \left| {{x_2}} \right| = 10 \)
\(\Leftrightarrow x_1^2 + x_2^2 + 2\left| {{x_1}{x_2}} \right| = 100\)
\(\Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + 2\left| {{x_1}{x_2}} \right| = 100\)
Lại có \({x_1}{x_2} = {m^2} + 3 > 0\;\forall m \) \(\Rightarrow \left| {{x_1}{x_2}} \right| = {x_1}{x_2} = {m^2} + 3.\)
Khi đó ta có: \(\left| {{x_1}} \right| + \left| {{x_2}} \right| = 10\)
\(\Leftrightarrow {\left( {\left| {{x_1}} \right| + \left| {{x_2}} \right|} \right)^2} = 100\)
\(\begin{array}{l} \Leftrightarrow x_1^2 + 2\left| {{x_1}{x_2}} \right| + x_2^2 = 100\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} + 2{x_1}{x_2} = 100\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} = 100\\ \Leftrightarrow {x_1} + {x_2} = \pm 10.\end{array}\)
+) TH1: \({x_1} + {x_2} = 10\) kết hợp với (2) ta được:
\(\left\{ \begin{array}{l}{x_1} + {x_2} = 10\\{x_1} + {x_2} = 2\left( {m + 1} \right)\end{array} \right. \)\(\,\Leftrightarrow 2\left( {m + 1} \right) = 10 \Leftrightarrow m = 4\left( {tm} \right)\)
+)TH2: \({x_1} + {x_2} = 10\) kết hợp với (2) ta được:
\(\left\{ \begin{array}{l}{x_1} + {x_2} = - 10\\{x_1} + {x_2} = 2\left( {m + 1} \right)\end{array} \right. \)\(\,\Leftrightarrow 2\left( {m + 1} \right) = - 10 \Leftrightarrow m = - 6\;\left( {ktm} \right)\)
Vậy \(m = 4\) thỏa mãn điều kiện bài toán.
Câu 3:
Một xe ô tô đi từ A đến B theo đường quốc lộ cũ dài 156 km với vận tốc không đổi. Khi từ B về A, xe đi đường cao tốc mới nên quãng đường giảm được 36 km so với lúc đi và vận tốc tăng so với lúc đi là 32 km/h. Tính vận tốc ô tô khi đi từ A đến B, biết thời gian đi nhiều hơn thời gian về là 1 giờ 45 phút.
Gọi vận tốc của ô tô khi đi từ A đến B là \(x\;\left( {km/h} \right)\;\;\left( {x > 0} \right).\)
Thời gian ô tô đi từ A đến B là: \(\dfrac{{156}}{x}\) (giờ).
Quãng đường lúc về là: \(156 - 36 = 120\left( {km} \right)\)
Vận tốc của ô tô lúc về là: \(x + 32\;\;\left( {km/h} \right).\) Thời gian của ô tô lúc về là: \(\dfrac{{120}}{{x + 32}}\) (giờ).
Đổi: 1 giờ 45 phút \( = 1 + \dfrac{{45}}{{60}} = \dfrac{7}{4}\) giờ.
Theo đề bài ta có phương trình: \(\dfrac{{156}}{x} - \dfrac{{120}}{{x + 32}} = \dfrac{7}{4}\)
\(\begin{array}{l} \Leftrightarrow 156.4.\left( {x + 32} \right) - 120.4.x = 7x\left( {x + 32} \right)\\ \Leftrightarrow 624x + 19968 - 480x = 7{x^2} + 224x\\ \Leftrightarrow 7{x^2} + 80x - 19968 = 0\\ \Leftrightarrow \left( {x - 48} \right)\left( {7x + 416} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 48 = 0\\7x + 416 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 48\;\;\left( {tm} \right)\\x = - \dfrac{{416}}{7}\;\;\left( {ktm} \right)\end{array} \right..\end{array}\)
Vậy vận tốc của ô tô lúc đi từ A đến B là \(48\;km/h.\)
Câu 4.
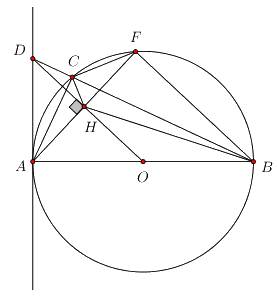
a) \(D{A^2} = DC.DB\)
Ta có \(\) (góc nội tiếp chắn nửa đường tròn tâm O) \( \Rightarrow AC \bot BC\,\,hay\,\,\,AC \bot BD\).
Ta có:\(\widehat {DAB} = {90^0}\) ( Do DA là tiếp tuyến của đường tròn tâm O tại A).
Áp dụng hệ thức lượng trong tam giác vuông ABD vuông tại A có đường cao AC ta có \(D{A^2} = DC.DB\).
b) Tứ giác AHCD nội tiếp.
Xét tứ giác AHCD có \(\widehat {AHD} = \widehat {ACD} = {90^0} \Rightarrow \) Hai đỉnh C và H kề nhau cùng nhìn cạnh AD dưới góc 900
\( \Rightarrow \) Tứ giác AHCD nội tiếp (Tứ giác có hai đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc bằng nhau).
c) \(CH \bot CF\)
Do tứ giác AHCD nội tiếp nên \(\widehat {FHC} = \widehat {ADC}\) (cùng bù với \(\widehat {AHC}\)).
Xét tam giác FHC và tam giác ADC có:
\(\widehat {CFH} = \widehat {DAC}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AC).
\(\widehat {FHC} = \widehat {ADC}\,\,\left( {cmt} \right)\);
Suy ra, tam giác FHC đồng dạng với tam giác ADC (g.g) => góc FCH bằng góc ACD (hai góc tương ứng)
Mà \(\widehat {ACD} = {90^0} \Rightarrow \widehat {FCH} = {90^0} \Rightarrow CH \bot CF\)
d) \(\dfrac{{BH.BC}}{{BF}} = 2R\)
Xét tam giác vuông OAD vuông tại A có OH là đường cao ta có \(O{A^2} = OD.OH\) (hệ thức lượng trong tam giác vuông)
Mà \(OA = OB = R \Rightarrow O{B^2} = OD.OH \)
\(\Rightarrow \dfrac{{OB}}{{OH}} = \dfrac{{OD}}{{OB}}\)
Xét tam giác OBH và ODB có:
\(\widehat {BOD}\) chung;
\(\dfrac{{OB}}{{OH}} = \dfrac{{OD}}{{OB}}\,\,\left( {cmt} \right)\);
Suy ra, tam giác OBH đồng dạng với tam giác ODB (c.g.c) => góc OBH bằng góc OBD
Mà \(\widehat {ODB} = \widehat {CAF}\) (hai góc nội tiếp cùng chắn cung CH của đường tròn ngoại tiếp tứ giác AHCD).
\(\widehat {CAF} = \widehat {CBF}\) (hai góc nội tiếp cùng chắn cung CF của đường tròn (O))
\( \Rightarrow \widehat {OBH} = \widehat {CBF} \)
\(\Rightarrow \widehat {OBH} + \widehat {HBC} = \widehat {CBF} + \widehat {HBC}\)
\(\Rightarrow \widehat {OBC} = \widehat {HBF} = \widehat {ABC}\)
Xét tam giác BHF và tam giác BAC có:
\(\widehat {BFH} = \widehat {BCA} = {90^0}\) (góc BFC nội tiếp chắn nửa đường tròn (O));
\(\widehat {HBF} = \widehat {ABC}\,\,\left( {cmt} \right)\);
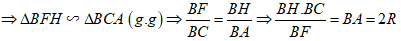
Câu 5.
Ta có: \(xy + 1 \le x,\,\,(x,y > 0) \Leftrightarrow y + \dfrac{1}{x} \le 1\)
Áp dụng BĐT Cô si, ta có: \(y + \dfrac{1}{x} \ge 2\sqrt {y.\dfrac{1}{x}} = 2\sqrt {\dfrac{y}{x}} \)
\(\Rightarrow 1 \ge 2\sqrt {\dfrac{y}{x}} \Leftrightarrow 0 < \dfrac{y}{x} \le \dfrac{1}{4}\)
\(Q = \dfrac{{x + y}}{{\sqrt {3{x^2} - xy + {y^2}} }} = \dfrac{{1 + \dfrac{y}{x}}}{{\sqrt {3 - \dfrac{y}{x} + \dfrac{{{y^2}}}{{{x^2}}}} }}\) . Đặt \(\dfrac{y}{x} = a,\,\,0 < a \le \dfrac{1}{4}\), ta có:
\(Q = \dfrac{{1 + a}}{{\sqrt {3 - a + {a^2}} }} = \sqrt {\dfrac{{{a^2} + 2a + 1}}{{{a^2} - a + 3}}} \) , \(0 < a \le \dfrac{1}{4}\)
Ta chứng minh: \(\dfrac{{{a^2} + 2a + 1}}{{{a^2} - a + 3}} \le \dfrac{5}{9}\,\,(*),\,\,\forall 0 < a \le \dfrac{1}{4}\)
\(\left( * \right) \Leftrightarrow 9({a^2} + 2a + 1) \le 5({a^2} - a + 3)\) ( do \({a^2} - a + 3 > 0,\,\,\forall a\))
\( \Leftrightarrow 4{a^2} + 23a - 6 \le 0 \)
\(\Leftrightarrow 4{a^2} - a + 24a - 6 \le 0\)
\(\Leftrightarrow a(4a - 1) + 6(4a - 1) \le 0\)
\(\Leftrightarrow (4a - 1)(a + 6) \le 0\)
Do \(0 < a \le \dfrac{1}{4}\) \( \Rightarrow 4a - 1 \le 0,\,\,a + 6 > 0 \Rightarrow (4a - 1)(a + 6) \le 0\)
\( \Rightarrow \dfrac{{{a^2} + 2a + 1}}{{{a^2} - a + 3}} \le \dfrac{5}{9}\,\,,\,\,\forall 0 < a \le \dfrac{1}{4}\)
\( \Rightarrow Q = \sqrt {\dfrac{{{a^2} + 2a + 1}}{{{a^2} - a + 3}}} \le \sqrt {\dfrac{5}{9}} = \dfrac{{\sqrt 5 }}{3}\),\(\forall 0 < a \le \dfrac{1}{4}\)
Vậy, \({Q_{max}} = \dfrac{{\sqrt 5 }}{3}\) khi và chỉ khi \(a = \dfrac{1}{4} \Leftrightarrow \left\{ \begin{array}{l}\dfrac{y}{x} = \dfrac{1}{4}\\y + \dfrac{1}{x} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = \dfrac{1}{2}\end{array} \right.\)
Đề số 5 - Đề thi vào lớp 10 môn Toán là một bài kiểm tra quan trọng giúp học sinh đánh giá năng lực và chuẩn bị tốt nhất cho kỳ thi tuyển sinh vào lớp 10. Bài viết này sẽ cung cấp phân tích chi tiết về cấu trúc đề thi, các dạng bài thường gặp, và hướng dẫn giải chi tiết từng câu hỏi.
Đề thi vào lớp 10 môn Toán thường bao gồm các phần sau:
Đề số 5 thường tập trung vào các chủ đề chính như đại số, hình học, và số học. Các câu hỏi có thể được kết hợp nhiều kiến thức khác nhau, đòi hỏi học sinh phải có sự hiểu biết sâu rộng và khả năng liên kết các khái niệm.
Trong đề thi vào lớp 10 môn Toán, các em thường gặp các dạng bài sau:
Để giúp các em hiểu rõ hơn về đề thi, chúng ta sẽ cùng nhau giải chi tiết một số câu hỏi trong Đề số 5 - Đề thi vào lớp 10 môn Toán.
Lời giải:
2x + 3 = 7
2x = 7 - 3
2x = 4
x = 2
Lời giải:
Diện tích hình vuông = cạnh * cạnh = 5cm * 5cm = 25cm2
Để chuẩn bị tốt nhất cho kỳ thi vào lớp 10 môn Toán, các em có thể tham khảo các tài liệu sau:
Đề số 5 - Đề thi vào lớp 10 môn Toán là một công cụ hữu ích giúp các em ôn tập và làm quen với cấu trúc đề thi. Hy vọng rằng, với những phân tích chi tiết và hướng dẫn giải trong bài viết này, các em sẽ tự tin hơn khi bước vào kỳ thi tuyển sinh vào lớp 10.