Bài 2 trang 88 SGK Toán 6 Cánh Diều Tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng thực hành phép tính với số nguyên. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 2 trang 88 SGK Toán 6 Cánh Diều Tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải bài tập.
Trong hình 10, hãy tính (theo mét):a) Khoảng cách giữa rặng san hô và người thợ lặn; b) Khoảng cách giữa người thợ lặn và mặt nước; c) Khoảng cách giữa mặt nước và con chim; d) Khoảng cách giữa rặng san hô và con chim.
Đề bài
Trong hình 10, hãy tính (theo mét):
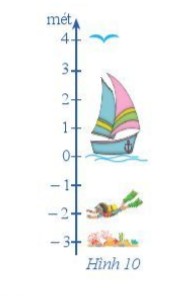
a) Khoảng cách giữa rặng san hô và người thợ lặn;
b) Khoảng cách giữa người thợ lặn và mặt nước;
c) Khoảng cách giữa mặt nước và con chim;
d) Khoảng cách giữa rặng san hô và con chim.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Tìm số nguyên biểu thị vị trí của con chim, mặt nước, người thợ lặn và rặng san hô.
- Trên trục số thằng đứng, số nằm bên trên lớn hơn các số nằm bên dưới nó.
- Cách tính khoảng cách: Lấy số lớn hơn trừ số nhỏ hơn.
Lời giải chi tiết
a)
Rặng san hô ở vị trí: (-3) mét
Người thợ lặn ở vị trí: (-2) mét
Người thợ lặn ở bên trên rặng san hô nên khoảng cách giữa hai đối tượng này là:
(– 2) – (- 3) = 1 mét.
b)
Mặt nước ở vị trí: 0 mét
Người thợ lặn ở vị trí: (-2) mét
Người thợ lặn ở bên dưới mặt nước nên khoảng cách giữa hai đối tượng này là:
0 – (- 2) = 2 mét.
c)
Con chim ở vị trí: 4 mét
Mặt nước ở vị trí: 0 mét
Con chim bên trên mặt nước nên khoảng cách giữa hai đối tượng này là:
4 – 0 = 4 mét.
d)
Con chim ở vị trí: 4 mét
Rặng san hô ở vị trí: (-3) mét
Con chim bên trên rặng san hô nên khoảng cách giữa hai đối tượng này là:
4 – (- 3) = 7 mét.
Bài 2 trang 88 SGK Toán 6 Cánh Diều Tập 1 thuộc chương học về số nguyên. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về số nguyên âm, số nguyên dương, và các phép toán cộng, trừ, nhân, chia số nguyên.
Bài 2 yêu cầu học sinh thực hiện các phép tính với số nguyên, bao gồm:
Các bài tập thường được trình bày dưới dạng các biểu thức số học hoặc các bài toán thực tế liên quan đến số nguyên.
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi qua từng phần của bài tập:
Để tính 5 + (-3), ta thực hiện phép cộng hai số nguyên khác dấu. Quy tắc là: cộng tổng các giá trị tuyệt đối và giữ dấu của số có giá trị tuyệt đối lớn hơn.
|5| = 5
|-3| = 3
5 - 3 = 2
Vì |5| > |-3|, nên kết quả là 2.
Vậy, 5 + (-3) = 2
Để tính (-7) - 2, ta thực hiện phép trừ hai số nguyên. Quy tắc là: trừ hai số nguyên bằng cách cộng số trừ với số đối của số bị trừ.
(-7) - 2 = (-7) + (-2)
|-7| = 7
|-2| = 2
7 + 2 = 9
Vì cả hai số đều âm, nên kết quả là -9.
Vậy, (-7) - 2 = -9
Để tính 4 x (-5), ta thực hiện phép nhân hai số nguyên khác dấu. Quy tắc là: nhân hai số nguyên khác dấu, kết quả là một số âm có giá trị tuyệt đối bằng tích của giá trị tuyệt đối của hai số đó.
|4| = 4
|-5| = 5
4 x 5 = 20
Vì 4 và -5 khác dấu, nên kết quả là -20.
Vậy, 4 x (-5) = -20
Để tính (-24) : 3, ta thực hiện phép chia hai số nguyên khác dấu. Quy tắc là: chia hai số nguyên khác dấu, kết quả là một số âm có giá trị tuyệt đối bằng thương của giá trị tuyệt đối của hai số đó.
|-24| = 24
|3| = 3
24 : 3 = 8
Vì -24 và 3 khác dấu, nên kết quả là -8.
Vậy, (-24) : 3 = -8
Số nguyên được sử dụng rộng rãi trong nhiều lĩnh vực của đời sống, như:
Việc hiểu rõ về số nguyên và các phép toán với số nguyên là rất quan trọng để giải quyết các bài toán thực tế và ứng dụng trong cuộc sống.
Bài 2 trang 88 SGK Toán 6 Cánh Diều Tập 1 là một bài tập cơ bản nhưng quan trọng để học sinh làm quen với các phép toán với số nguyên. Bằng cách nắm vững các quy tắc và thực hành thường xuyên, học sinh có thể tự tin giải quyết các bài tập tương tự và ứng dụng kiến thức vào thực tế.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải Bài 2 trang 88 SGK Toán 6 Cánh Diều Tập 1 và đạt kết quả tốt trong môn Toán.