Chào mừng các em học sinh đến với bài học về Lý thuyết Hình có trục đối xứng trong chương trình Toán 6 Cánh diều.
Bài học này sẽ giúp các em hiểu rõ khái niệm về trục đối xứng, cách nhận biết hình có trục đối xứng và các tính chất quan trọng của chúng.
Lý thuyết Hình có trục đối xứng Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
1. Hình có trục đối xứng
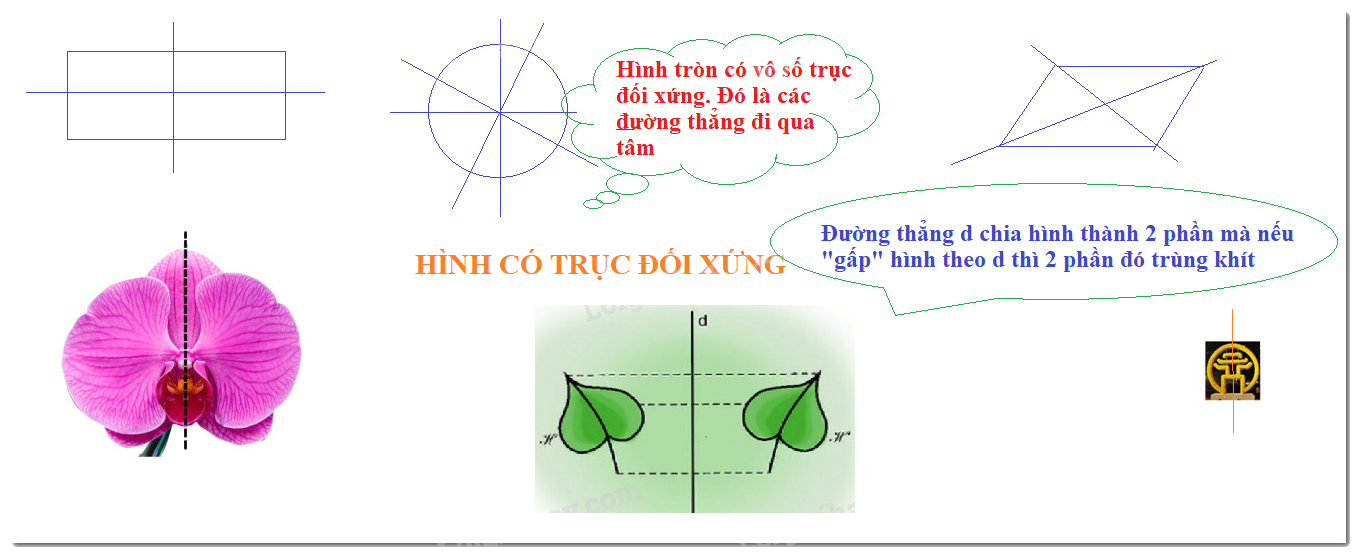
Có một đường thẳng d chia hình thành hai phần mà khi ta “gấp” hình theo đường thẳng d thì hai phần đó “chồng khít” lên nhau.
Những hình như thế là hình có trục đối xứng và đường thẳng d là trục đối xứng của nó.
2. Trục đối xứng của một số hình
Ví dụ:
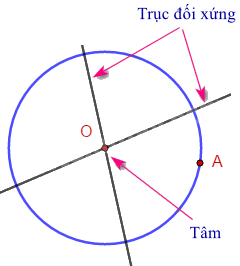
- Đường tròn: Mỗi đường thẳng đi qua tâm là một trục đối xứng.
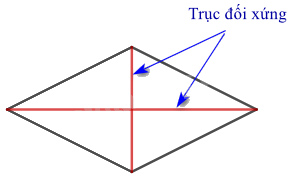
- Hình thoi: Mỗi đường chéo là một trục đối xứng.
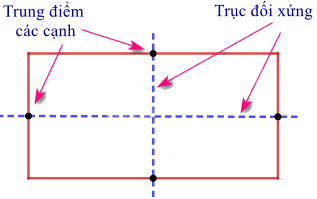
- Hình chữ nhật: Mỗi đường thẳng đi qua trung điểm hai cạnh đối diện là một trục đối xứng của hình chữ nhật.
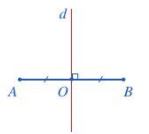
- Đoạn thẳng AB là hình có trục đối xứng và trục đối xứng là đường thẳng d đi qua trung
điểm 0 của đoạn thẳng AB và vuông góc với AB.
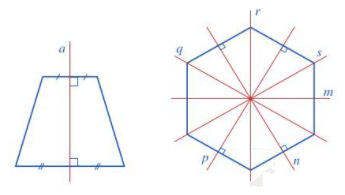
- Hình thang cân có 1 trục đối xứng là đường thẳng a
Hình lục giác đều có 6 trục đối xứng là các đường thẳng m, n, p, q, r, s.
Trong chương trình Toán 6, chủ đề Hình có trục đối xứng đóng vai trò quan trọng trong việc phát triển tư duy hình học và khả năng quan sát của học sinh. Bài viết này sẽ cung cấp một cách đầy đủ và chi tiết về lý thuyết này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập liên quan.
Một đường thẳng được gọi là trục đối xứng của một hình nếu hình đó khi bị gấp theo đường thẳng đó thì hai phần của hình trùng khít lên nhau. Nói cách khác, mọi điểm trên hình đều có một điểm tương ứng nằm đối xứng qua trục đối xứng.
Một hình được gọi là hình có trục đối xứng nếu nó có ít nhất một trục đối xứng. Một hình có thể có nhiều trục đối xứng, thậm chí là vô số trục đối xứng.
Để nhận biết một hình có trục đối xứng, ta có thể thực hiện các bước sau:
Hình có trục đối xứng có những tính chất sau:
Bài 1: Hình nào sau đây có trục đối xứng?
Bài 2: Vẽ hình vuông ABCD và chỉ ra các trục đối xứng của nó.
Hình có trục đối xứng xuất hiện rất nhiều trong thực tế, ví dụ như:
Ngoài khái niệm về trục đối xứng, các em học sinh cũng nên tìm hiểu thêm về khái niệm đối xứng tâm, đối xứng qua một điểm. Đây là những kiến thức quan trọng giúp các em hiểu sâu hơn về hình học.
Hy vọng bài viết này đã cung cấp cho các em những kiến thức cơ bản và hữu ích về Lý thuyết Hình có trục đối xứng Toán 6 Cánh diều. Chúc các em học tập tốt!