Chào mừng các em học sinh đến với bài học về Lý thuyết Phép nhân số nguyên Toán 6 Cánh diều tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về phép nhân số nguyên, giúp các em tự tin giải các bài tập liên quan.
Chúng ta sẽ cùng nhau tìm hiểu về quy tắc nhân hai số nguyên, các trường hợp đặc biệt và ứng dụng của phép nhân trong thực tế.
Lý thuyết Phép nhân số nguyên Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
1.Nhân hai số nguyên khác dấu
Để nhân hai số nguyên khác dấu, ta làm như sau:
Bước 1: Bỏ dấu “-” trước số nguyên âm, giữ nguyên số còn lại
Bước 2: Tính tích của hai số nguyên dương nhận được ở Bước 1
Bước 3: Thêm dấu “-” trước kết quả nhận được ở Bước 2, ta có kết quả cần tìm.
Nhận xét: Tích của hai số nguyên khác dấu là số nguyên âm.
Chú ý:
Cho hai số nguyên dương \(a\) và \(b\), ta có:
\(\left( { + a} \right).\left( { - b} \right) = - a.b\)
\(\left( { - a} \right).\left( { + b} \right) = - a.b\)
Ví dụ:
a) \(( - 20).5 = - \left( {20.5} \right) = - 100.\)
b) \(15.\left( { - 10} \right) = - \left( {15.10} \right) = - 150.\)
c) \(20.\left( { + 50} \right) + 4.\left( { - {\rm{ }}40} \right) = 1000 - (4.40) = 1000 - 160 = 840. \)
2.Nhân hai số nguyên cùng dấu
Để nhân hai số nguyên âm, ta làm như sau:
Để nhân hai số nguyên âm, ta làm như sau:
Bước 1: Bỏ dấu “-” trước mỗi số
Bước 2: Tính tích của hai số nguyên dương nhận được ở Bước 1, ta có tích cần tìm.
Nhận xét:
- Khi nhân hai số nguyên dương, ta nhân chúng như nhân hai số tự nhiên.
- Tích của hai số nguyên cùng dấu là số nguyên dương.
Chú ý:
Cho hai số nguyên dương \(a\) và \(b\), ta có:
\(\left( { - a} \right).\left( { - b} \right) = ( + a).( + a) = a.b\)
\(\left( { - a} \right).\left( { + b} \right) = - a.b\)
Ví dụ:
a) \(( - 4).( - 15) = 4.15 = 60\)
b) \(\left( { + 2} \right).( + 5) = 2.5 = 10\).
Phép nhân các số nguyên có các tính chất:
+) Giao hoán: \(a.b = b.a\)
+) Kết hợp: \(a\left( {bc} \right) = \left( {ab} \right)c\)
+) Phân phối đối với phép cộng: \(a\left( {b + c} \right) = ab + ac\)
+) Phân phối đối với phép trừ: \(a\left( {b - c} \right) = ab - ac\)
Nhận xét:
Trong một tích nhiều thừa số ta có thể:
- Đổi chỗ hai thừa số tùy ý.
- Dùng dấu ngoặc để nhóm các thừa số một cách tùy ý:
Chú ý:
+) \(a.1 = 1.a = a\)
+) \(a.0 = 0.a = 0\)
+) Cho hai số nguyên \(x,\,\,y\):
Nếu \(x.y = 0\) thì \(x = 0\) hoặc \(y = 0\).
Ví dụ 1:
a) \(\left( { - 3} \right).5 = 5.\left( { - 3} \right) = - 15\)
b) \(\left[ {\left( { - 2} \right).7} \right].\left( { - 3} \right) = \left( { - 2} \right).\left[ {7.\left( { - 3} \right)} \right] = \left( { - 2} \right).\left( { - 21} \right) = 42\)
c) \(\left( { - 5} \right).12 + \left( { - 5} \right).88 = \left( { - 5} \right).\left( {12 + 88} \right) = \left( { - 5} \right).100 = - 500\).
d) \(\left( { - 9} \right).36 - ( - 9).26 = \left( { - 9} \right).\left( {36 - 26} \right) = \left( { - 9} \right).10 = - 90\)
Ví dụ 2:
Nếu \(\left( {x - 1} \right)\left( {x + 5} \right) = 0\) thì \(x - 1 = 0\) hoặc \(x + 5 = 0\).
Suy ra \(x = 1\) hoặc \(x = - 5\).
Chú ý:
+ Nhờ tính chất kết hợp ta có tích của ba, bốn, năm… số nguyên.
+ Khi thực hiện phép nhân nhiều số nguyên, ta có thể dựa vào các tính chất giao hoán và kết hợp để thay đổi vị trí giữa các thừa số, đặt dấu ngoặc để nhóm các thừa số thích hợp.
+ Tích của \(n\) số nguyên \(a\) là lũy thừa bậc \(n\) của số nguyên \(a.\)
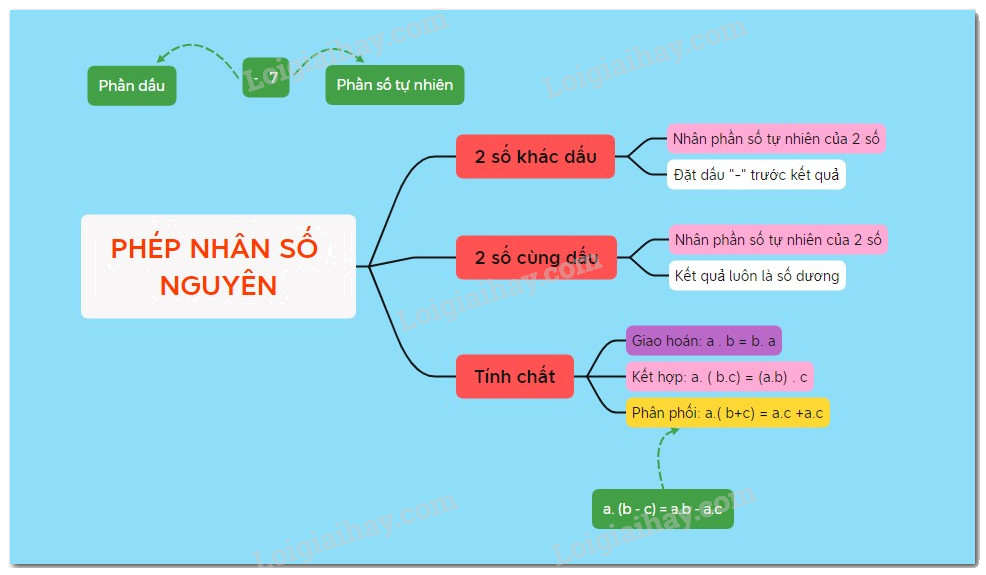
Phép nhân số nguyên là một trong những phép toán cơ bản trong toán học, đặc biệt quan trọng ở chương trình Toán 6. Hiểu rõ lý thuyết và quy tắc của phép nhân số nguyên là nền tảng để giải quyết các bài toán phức tạp hơn trong tương lai.
Phép nhân số nguyên là phép toán thực hiện trên các số nguyên, bao gồm số nguyên dương, số nguyên âm và số 0. Phép nhân hai số nguyên được ký hiệu bằng dấu 'x'.
Quy tắc nhân hai số nguyên là một trong những nội dung quan trọng nhất cần nắm vững. Dưới đây là quy tắc chi tiết:
Phép nhân số nguyên có những tính chất quan trọng sau:
Hãy cùng xem xét một số ví dụ để hiểu rõ hơn về cách áp dụng quy tắc và tính chất của phép nhân số nguyên:
Áp dụng quy tắc nhân hai số nguyên khác dấu, ta có: (-6) x (+4) = -24
Áp dụng quy tắc nhân hai số nguyên khác dấu, ta có: (+9) x (-2) = -18
Áp dụng quy tắc nhân hai số nguyên cùng dấu, ta có: (-5) x (-7) = +35
Để củng cố kiến thức, hãy thực hiện các bài tập sau:
| STT | Bài tập | Đáp án |
|---|---|---|
| 1 | (+8) x (-3) = ? | -24 |
| 2 | (-4) x (+6) = ? | -24 |
| 3 | (-2) x (-9) = ? | +18 |
Phép nhân số nguyên được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như:
Khi thực hiện phép nhân số nguyên, cần chú ý đến dấu của các số hạng. Việc xác định đúng dấu của kết quả là rất quan trọng để tránh sai sót.
Hy vọng bài học về Lý thuyết Phép nhân số nguyên Toán 6 Cánh diều này sẽ giúp các em hiểu rõ hơn về phép toán quan trọng này. Chúc các em học tập tốt!