Bài học này cung cấp kiến thức nền tảng về phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố. Đây là một trong những kiến thức quan trọng của chương trình Toán 6, giúp học sinh hiểu rõ hơn về cấu trúc của các số tự nhiên.
Chúng ta sẽ cùng tìm hiểu định nghĩa, tính chất và phương pháp phân tích một số ra thừa số nguyên tố một cách chi tiết và dễ hiểu nhất.
Lý thuyết Phân tích một số ra thừa số nguyên tố Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
I. Cách tìm một ước nguyên tố của một số:
Để tìm một ước nguyên tố của số tự nhiên n lớn hơn 1, ta có thể làm như sau: Lần lượt làm phép chia n cho các số nguyên tố theo thứu tự tăng dần: 2;3;5;7;11;13;...
Khi đó, phép chia hết đầu tiên cho ta số chia là một ước nguyên tố của n
II.Phân tích một số ra thừa số nguyên tố
- Phân tích một số tự nhiên lớn hơn \(1\) ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
- Viết các thừa số nguyên tố theo thứ tự từ bé đến lớn, tích các thừa số giống nhau dưới dạng lũy thừa.
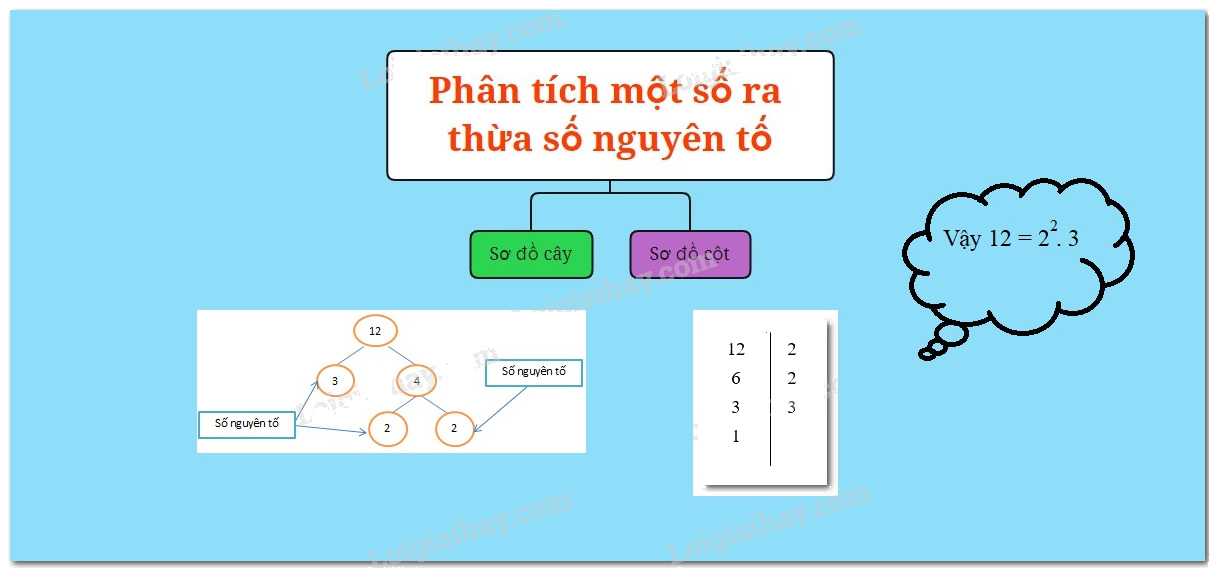
Sơ đồ cây:
Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.
Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.
Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.
Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.
Ví dụ:
Phân tích số 12 ra thừa số nguyên tố bằng sơ đồ cây:
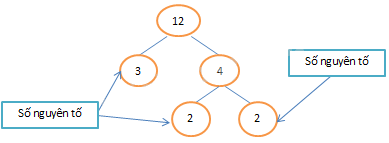
Như vậy \(12 = {2^2}.3\)
Sơ đồ cột:
Chia số \(n\) cho một số nguyên tố (xét từ nhỏ đến lớn ), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng \(1.\)
Ví dụ: Số \(76\) được phân tích như sau:
\[76\] | \[2\] |
\[38\] | \[2\] |
\[19\] | \[19\] |
\[1\] |
Như vậy \(76 = {2^2}.19\)
CÁC DẠNG TOÁN VỀ PHÂN TÍCH MỘT SỐ RA THỪA SỐ NGUYÊN TỐ
Phương pháp:
Ta thường phân tích một số tự nhiên $n\left( {n > 1} \right)$ ra thừa số nguyên tố bằng 2 cách:
+ Sơ đồ cây
+ Phân tích theo hàng dọc.
Phương pháp:
+ Phân tích số cho trước ra thừa số nguyên tố.
+ Chú ý rằng nếu $c = a.b$ thì $a$ và $b$ là hai ước của $c.$
$a = b.q$\( \Leftrightarrow a \vdots b \Leftrightarrow a \in B\left( b \right)\) và \(b \in \)Ư\(\left( a \right)\) $(a,b,q \in N,b \ne 0)$
Phương pháp:
Phân tích đề bài, đưa về việc tìm ước của một số cho trước bằng cách phân tích số đó ra thừa số nguyên tố.
Phân tích một số ra thừa số nguyên tố là một kỹ năng toán học cơ bản nhưng vô cùng quan trọng trong chương trình Toán 6. Nó không chỉ giúp học sinh hiểu sâu hơn về cấu trúc của các số tự nhiên mà còn là nền tảng cho nhiều kiến thức toán học nâng cao hơn.
Một số tự nhiên lớn hơn 1 được gọi là số nguyên tố nếu chỉ chia hết cho 1 và chính nó. Ví dụ: 2, 3, 5, 7, 11,...
Thừa số nguyên tố của một số là một số nguyên tố chia hết cho số đó. Ví dụ, thừa số nguyên tố của 12 là 2 và 3.
Phân tích một số ra thừa số nguyên tố là việc biểu diễn số đó dưới dạng tích của các thừa số nguyên tố. Ví dụ, 12 = 22 * 3.
Có nhiều phương pháp để phân tích một số ra thừa số nguyên tố, nhưng phương pháp phổ biến nhất là sử dụng sơ đồ cây:
Ví dụ: Phân tích 36 ra thừa số nguyên tố
Vậy, 36 = 22 * 32
Hãy phân tích các số sau ra thừa số nguyên tố:
Đáp án:
Khi phân tích một số ra thừa số nguyên tố, cần lưu ý:
Việc phân tích một số ra thừa số nguyên tố có nhiều ứng dụng trong toán học, bao gồm:
Lý thuyết phân tích một số ra thừa số nguyên tố là một kiến thức quan trọng trong chương trình Toán 6. Việc nắm vững lý thuyết và phương pháp phân tích sẽ giúp học sinh giải quyết các bài toán một cách dễ dàng và hiệu quả hơn. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng của mình.
| Số | Phân tích ra thừa số nguyên tố |
|---|---|
| 10 | 2 * 5 |
| 15 | 3 * 5 |
| 20 | 22 * 5 |
| Bảng ví dụ phân tích một số ra thừa số nguyên tố | |