Bài học về Hình có tâm đối xứng trong chương trình Toán 6 Cánh diều là nền tảng quan trọng để học sinh hiểu về tính đối xứng trong hình học. Nắm vững lý thuyết này giúp các em giải quyết các bài tập liên quan một cách dễ dàng và chính xác.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng để hỗ trợ học sinh học tập hiệu quả.
Lý thuyết Hình có tâm đối xứng Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
1. Hình có tâm đối xứng
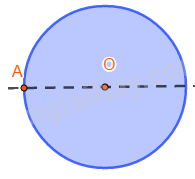
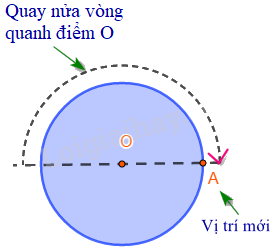
Những hình có một điểm O sao cho khi quay nửa vòng quanh điểm O ta được vị trí mới của hình chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.
Ví dụ:+ Các hình tròn và chong chóng bốn cánh dưới đây là các hình có tâm đối xứng vì khi quay nửa vòng quanh điểm O thì hình thu được chồng khít với chính nó ở vị trí ban đầu.
+ Ta thấy hình chong chóng ba cánh khi quay nửa vòng quanh điểm O thì hình thu được không chồng khít với chính nó ở vị trí ban đầu => Hình này không có tâm đối xứng.
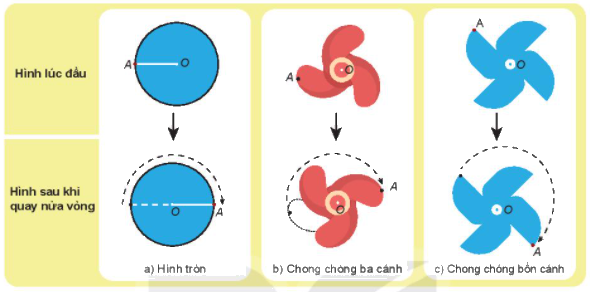
Ví dụ: Hình có tâm đối xứng là các hình: hình tròn, hình chong chóng 2 cánh, chong chóng 4 cánh,...
2. Tâm đối xứng của một số hình
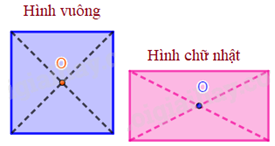
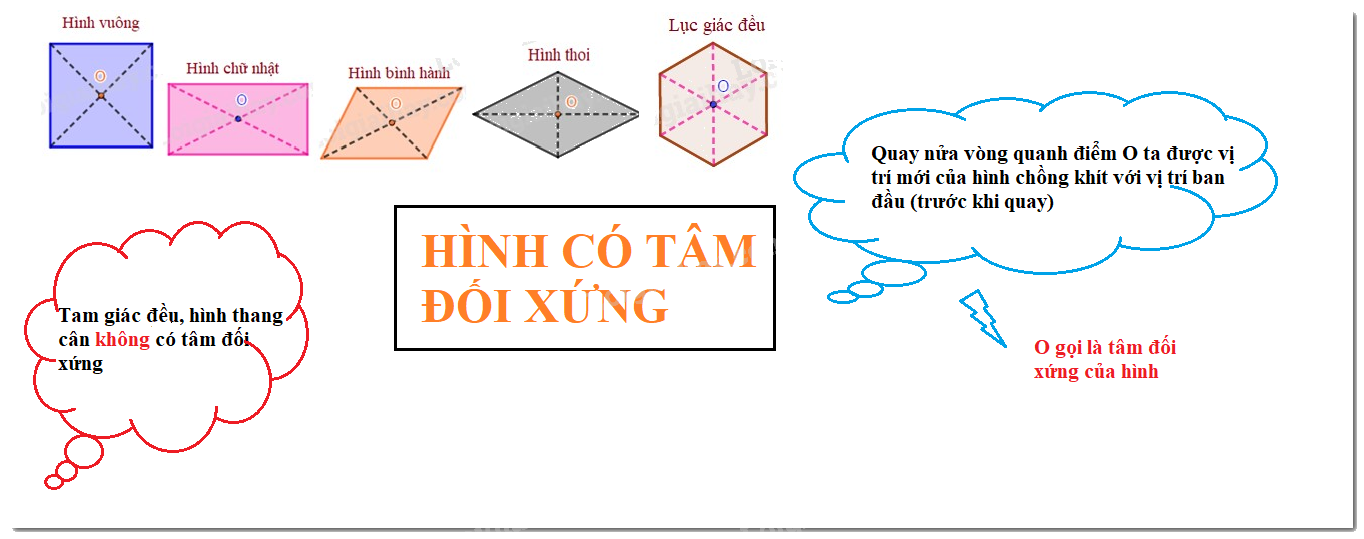
Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.
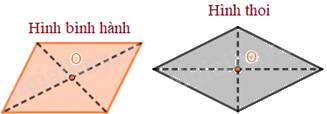
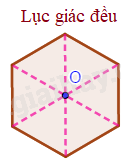
Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
Lưu ý:
- Có những hình có tâm đối xứng và có nhiều trục đối xứng: Hình tròn, hình vuông, hình chữ nhật, hình thoi.
- Có hình không có tâm đối xứng: Tam giác đều, hình thang cân,..
Trong chương trình Toán 6, phần Hình học đóng vai trò quan trọng trong việc phát triển tư duy logic và khả năng quan sát của học sinh. Một trong những khái niệm cơ bản và thú vị nhất là khái niệm về Hình có tâm đối xứng. Bài viết này sẽ cung cấp một cách đầy đủ và chi tiết về lý thuyết này, dựa trên chương trình Toán 6 Cánh diều.
Một hình được gọi là có tâm đối xứng nếu có một điểm O (gọi là tâm đối xứng) sao cho mọi điểm M của hình đều có một điểm M’ đối xứng với M qua O, và M’ cũng thuộc hình đó.
Nói cách khác, nếu bạn xoay một hình 180 độ quanh tâm đối xứng O, hình đó vẫn giữ nguyên.
Để tìm tâm đối xứng của một hình, bạn có thể thực hiện các bước sau:
Ví dụ 1: Hình vuông ABCD có tâm đối xứng là giao điểm O của hai đường chéo AC và BD. Điều này có nghĩa là nếu bạn xoay hình vuông 180 độ quanh điểm O, hình vuông vẫn giữ nguyên.
Ví dụ 2: Hình tròn có tâm O. Bất kỳ điểm M nào trên đường tròn đều có điểm M’ đối xứng qua O, và M’ cũng nằm trên đường tròn.
Hãy xác định tâm đối xứng (nếu có) của các hình sau:
Phép đối xứng tâm là phép biến hình biến mỗi điểm M thành điểm M’ sao cho O là trung điểm của đoạn thẳng MM’. Tâm đối xứng của một hình là tâm của phép đối xứng tâm biến hình đó thành chính nó.
Khái niệm về hình có tâm đối xứng được ứng dụng rộng rãi trong thực tế, ví dụ như:
Để nắm vững hơn về lý thuyết Hình có tâm đối xứng, bạn có thể thực hành thêm các bài tập sau:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về Lý thuyết Hình có tâm đối xứng Toán 6 Cánh diều. Chúc bạn học tập tốt!