Chào mừng các em học sinh đến với bài học về Lý thuyết Bội chung và bội chung nhỏ nhất trong chương trình Toán 6 Cánh diều. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng về các khái niệm này, cùng với các ví dụ minh họa cụ thể.
Nắm vững lý thuyết này là nền tảng để giải quyết các bài toán liên quan đến số học, đặc biệt là trong các bài kiểm tra và thi cử. Hãy cùng giaitoan.edu.vn khám phá bài học này một cách hiệu quả nhất!
Lý thuyết Bội chung và bội chung nhỏ nhất Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
1. Định nghĩa
Bội chung của hai hay nhiều số là bội của tất cả các số đó.
2. Kí hiệu
+ BC\(\left( {a,b} \right)\) là tập hợp các bội chung của \(a\) và \(b\).
3. Cách tìm bội chung
a) Tìm bội chung của hai số a và b
Bước 1: Viết tập hợp các bội B(a) của a và các bội B(b) của b.
Bước 2: Tìm những phần tử chung của B(a) và B(b).
Ví dụ: \(B\left( 3 \right) = \left\{ {0;3;6;9;12;...} \right\}\); \(B\left( 2 \right) = \left\{ {0;2;4;6;8;10;12;...} \right\}\)
Nên \(BC\left( {2,3} \right) = \left\{ {0;6;12;...} \right\}\)
b) Tìm bội chung của ba số a, b và c
Bước 1: Viết tập hợp các bội của a, của b và của c: B(a), B(b), B(c)
Bước 2: Tìm những phần tử chung của B(a), B(b) và B(c).
Nhận xét:
+) \(x \in BC\left( {a;b} \right)\) nếu \(x \vdots a\) và \(x \vdots b\)
+) \(x \in BC\left( {a;b;c} \right)\) nếu \(x \vdots a\); \(x \vdots b\) và \(x \vdots c\)
Chú ý:
+ Ta chỉ xét bội chung của các số khác 0.
+ Giao của hai tập hợp là một tập hợp gồm các phần tử chung của hai tập hợp đó.
+ Kí hiệu: Giao của tập hợp A và tập hợp B là \(A \cap B\)
Ví dụ:\(B\left( 2 \right) \cap B\left( 3 \right) = BC\left( {2;3} \right)\)
1. Định nghĩa
Bội chung nhỏ nhất (BCNN) của hai hay nhiều số là số nhỏ nhấtkhác 0 trong tập hợp các bội chung của các số đó..
2.Kí hiệu
+) \(BCNN\left( {a,b} \right)\) là bội chung nhỏ nhất của \(a\) và \(b\).
+) BC\(\left( {a,b} \right)\) là tập hợp còn BCNN\(\left( {a,b} \right)\) là một số.
3. Cách tìm bội chung lớn nhất bằng định nghĩa
a) Cách tìm bội chung nhỏ nhất trong các trường hợp đặc biệt
Nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho là số lớn nhất đó.
Nếu \(a \vdots b\) thì \(BCNN\left( {a,b} \right) = a\)
Với mọi số tự nhiên a và b ta có:
\(BCNN\left( {a,1} \right) = a;\)\(BCNN\left( {a,b,1} \right) = BCNN\left( {a,b} \right)\)
Ví dụ:
Bội chung nhỏ nhất của 12 và 36 là 12 vì \(36 \vdots 12\).
b) Cách tìm BCNN của hai số a và b bằng định nghĩa
Bước 1. Tìm tập hợp các bội chung của hai số a và b: BC\(\left( {a,b} \right)\)
Bước 2. Tìm số nhỏ nhất khác 0 trong các bội chung vừa tìm được: BCNN\(\left( {a,b} \right)\)
Ví dụ : Tìm BCNN (15 ; 20)
\(\begin{array}{l}B\left( {15} \right) = \left\{ {0;15;30;45;60;75;90;105;120;..} \right\}\\B\left( {20} \right) = \left\{ {0;20;40;60;80;100;120;...} \right\}\\BC\left( {15,20} \right) = \left\{ {0;60;120;...} \right\}\end{array}\)
Số nhỏ nhất khác 0 trong các bội chung trên là 60 nên BCNN (15 , 20)=60.
1. Cách tìm bội chung nhỏ nhất-BCNN
Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện theo ba bước sau :
Bước 1 : Phân tích mỗi số ra thừa số nguyên tố.
Bước 2 : Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3 : Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
Ví dụ: Tìm BCNN của \(15\) và \(20.\)
Ta có \(15 = 3.5;20 = {2^2}.5\)
Nên \(BCNN\left( {15,20} \right) = {2^2}.3.5 = 60.\)
2. Cách tìm bội chung thông qua bội chung nhỏ nhất
Để tìm bội chung của các số đã cho, ta có thể tìm các bội của BCNN của các số đó.
Ví dụ: \(BCNN\left( {15,20} \right) = 60\) nên \(BC\left( {15,20} \right) = B\left( {60} \right) = \left\{ {0;60;120;...} \right\}\)
Tìm mẫu chung của hai phân số
Cách 1: Chọn mẫu chung cho hai phân số là bội chung nhỏ nhất của hai mẫu số đó.
Cách 2: Chọn bội chung bất kì khác 0 của 2 mẫu số đó.
Ví dụ:Quy đồng mẫu số hai phân số \(\dfrac{7}{{30}}\) và \(\dfrac{5}{{42}}\)
\(\begin{array}{l}30 = 2.3.5\\42 = 2.3.7\end{array}\)
\(\begin{array}{l} \Rightarrow BCNN\left( {30;42} \right) = 2.3.5.7 = 210\\ \Rightarrow BC\left( {30;42} \right) = \left\{ {0;210;420;...} \right\}\end{array}\)
+) Cách 1: Chọn mẫu chung là 210. Ta được:
\(\begin{array}{l}\dfrac{7}{{30}} = \dfrac{{7.7}}{{210}} = \dfrac{{49}}{{210}}\\\dfrac{5}{{42}} = \dfrac{{5.5}}{{42.5}} = \dfrac{{25}}{{210}}\end{array}\)
+) Cách 2: Chọn mẫu chung là một bội chung bất kì khác 0 của 30 và 42. Chẳng hạn 420, ta được:
\(\begin{array}{l}\dfrac{7}{{30}} = \dfrac{{7.14}}{{30.14}} = \dfrac{{98}}{{420}}\\\dfrac{5}{{42}} = \dfrac{{5.10}}{{42.10}} = \dfrac{{50}}{{420}}\end{array}\)
Phương pháp:
+ Để nhận biết một số là bội chung của hai số, ta kiểm tra xem số này có chia hết cho hai số đó hay không?
+ Để viết tập hợp các bội chung của hai hay nhiều số, ta viết tập hợp các bội của mỗi số rồi tìm giao của các tập hợp đó.
Phương pháp:
Phân tích đề bài, suy luận để đưa về việc tìm BC, BCNN của hai hay nhiều số.
Ví dụ:
Có hai chiếc máy bay A và B. Lịch bảo dưỡng định kì đối với máy A là 6 tháng và đối với máy B là 9 tháng. Hai máy vừa cùng được bảo dưỡng vào tháng 5. Hỏi sau ít nhất bao nhiêu tháng nữa thì hai máy lại được bảo dưỡng trong cùng một tháng.
Giải
Thời gian hai máy bay được bảo dưỡng cùng nhau trong lần tiếp theo là BCNN của 6 và 9.
Ta có: BCNN(6, 9)= 36
Vậy sau ít nhất 36 tháng thì hai máy bay lại được bảo dưỡng trong cùng một tháng.
Phương pháp:
+ Tìm BCNN của hai hay nhiều số cho trước.
+ Tìm các bội của BCNN.
+ Chọn trong số đó các ước hoặc các bội thỏa mãn điều kiện đã cho.
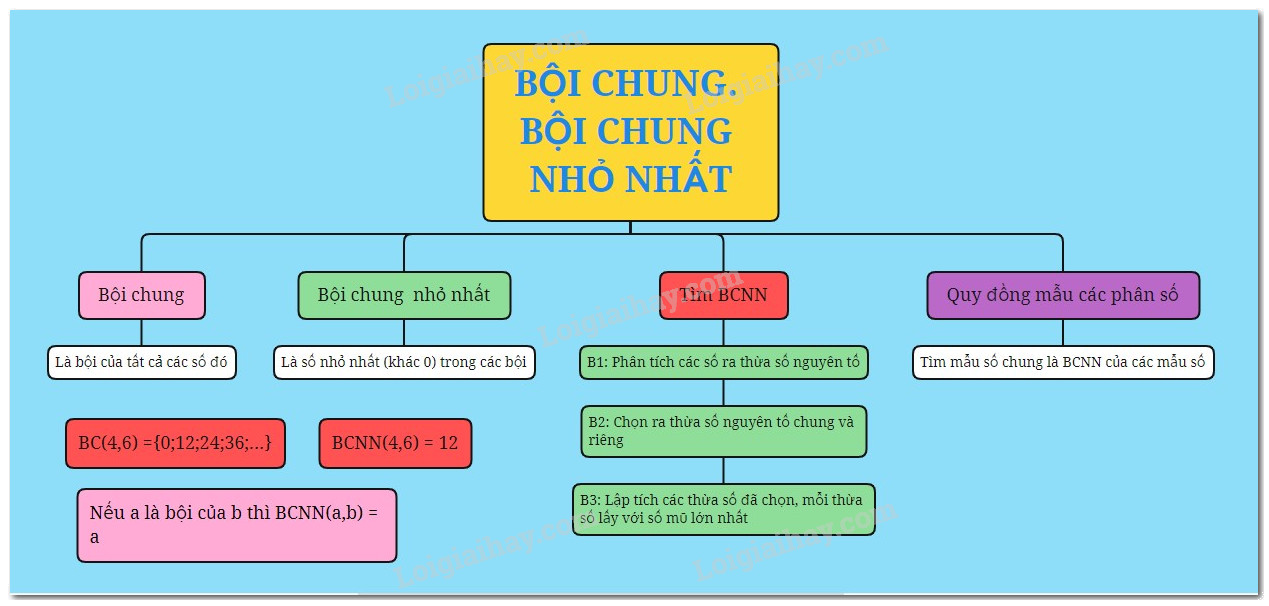
Bài học này sẽ trình bày chi tiết về khái niệm bội chung, bội chung nhỏ nhất (BCNN) và cách tìm BCNN của hai hay nhiều số. Chúng ta sẽ cùng nhau tìm hiểu các phương pháp khác nhau để xác định BCNN, bao gồm phương pháp liệt kê, phương pháp phân tích ra thừa số nguyên tố và ứng dụng của BCNN trong giải toán.
Bội chung của hai hay nhiều số là số chia hết cho tất cả các số đó. Ví dụ, bội chung của 2 và 3 là 6, 12, 18,...
BCNN của hai số a và b, ký hiệu là BCNN(a, b), là số nhỏ nhất mà cả a và b đều chia hết.
Ví dụ: BCNN(4, 6) = 12
Ví dụ 1: Tìm BCNN(8, 12)
Giải:
Ví dụ 2: Tìm BCNN(15, 20, 25)
Giải:
BCNN được sử dụng trong nhiều bài toán thực tế, chẳng hạn như:
Hãy tự giải các bài tập sau để củng cố kiến thức:
Hy vọng bài học này đã giúp các em hiểu rõ hơn về Lý thuyết Bội chung và bội chung nhỏ nhất Toán 6 Cánh diều. Chúc các em học tập tốt!