Chào mừng các em học sinh đến với bài học về lý thuyết Tam giác đều, Hình vuông, Lục giác đều trong chương trình Toán 6 Cánh diều. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về các hình đa giác đều này.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất, cách vẽ và các ứng dụng thực tế của từng hình. Mục tiêu là giúp các em hiểu rõ bản chất của các hình này và có thể áp dụng vào giải các bài tập một cách hiệu quả.
Lý thuyết Tam giác đều. Hình vuông. Lục giác đều Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
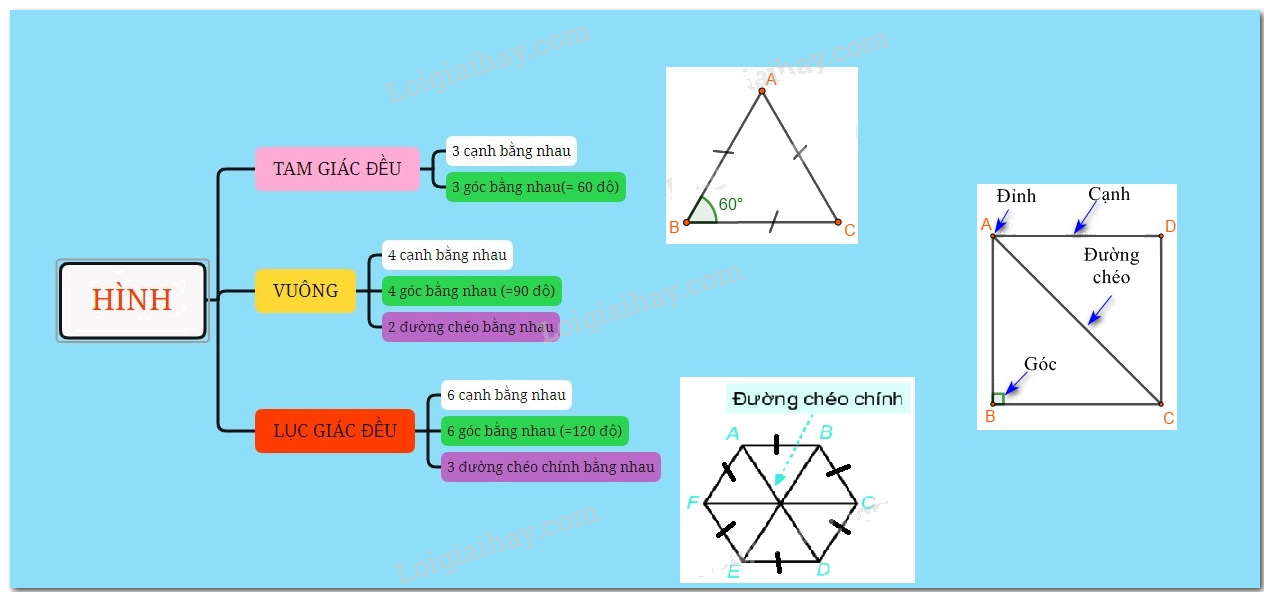
1. Hình tam giác đều
Các yếu tố cơ bản của tam giác đều:
- Ba cạnh bằng nhau.
- Ba góc bằng nhau và bằng \({60^0}\)
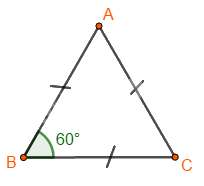
Cách vẽ tam giác đều \(ABC\) khi biết độ dài một cạnh bằng \(a\).
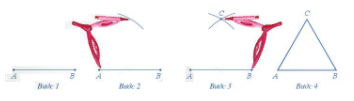
Bước 1: Dùng thước vẽ đoạn thẳng AB=a cm
Bước 2: Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB
Bước 3: Lây B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA. Gọi C là giao điểm của 2 đường tròn vừa vẽ
Bước 4: Dùng thước vẽ các đoạn thẳng AC và BC
2. Hình vuông
Một số yếu tố cơ bản của hình vuông
- Bốn cạnh bằng nhau.
- Bốn góc bằng nhau và bằng \({90^0}\).
- Hai đường chéo bằng nhau.
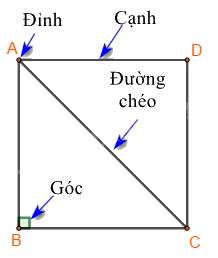
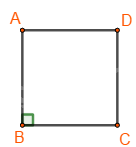
Ví dụ: Cho hình vuông ABCD
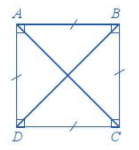
Bốn cạnh bằng nhau: \(AB = BC = CD = DA;\)
Hai cạnh đối \(AB\) và \(CD;\) \(AD\) và \(BC\) song song với nhau;
Hai đường chéo bằng nhau: \(AC = BD;\)
Bốn góc ở các đỉnh \(A,{\rm{ }}B,{\rm{ }}C,{\rm{ }}D\) là góc vuông.
Cách vẽ hình vuông khi biết độ dài cạnh bằng \(a\):
Bước 1: Vẽ đoạn thẳng \(AB = a\left( {cm} \right)\)
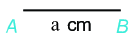
Bước 2: Vẽ đường thẳng vuông góc với \(AB\) tại \(A\). Xác định điểm \(D\) trên đường thẳng đó sao cho \(AD = a\left( {cm} \right)\).
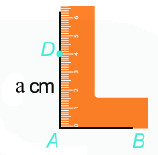
Bước 3: Vẽ đường thẳng vuông góc với \(AB\) tại \(B\). Xác định điểm \(C\) trên đường thẳng đó sao cho \(BC = a\left( {cm} \right)\).
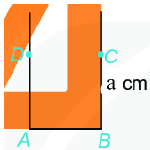
Bước 4: Nối \(C\) với \(D\) ta được hình vuông \(ABCD\).
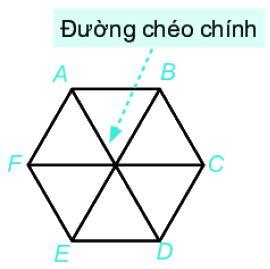
3. Hình lục giác đều
Một số yếu tố cơ bản của hình lục giác đều:
- Sáu cạnh bằng nhau.
- Sáu góc bằng nhau và bằng \({120^0}\).
- Ba đường chéo chính bằng nhau.
- AC, BD, CE, DF, EA,FB là các đường chéo phụ của ABCDEF.
Trong chương trình Toán 6, việc nắm vững kiến thức về các hình đa giác đều như Tam giác đều, Hình vuông và Lục giác đều là vô cùng quan trọng. Đây là nền tảng để các em học sinh tiếp cận với những kiến thức hình học phức tạp hơn ở các lớp trên.
Định nghĩa: Tam giác đều là tam giác có ba cạnh bằng nhau.
Tính chất:
Cách vẽ:
Định nghĩa: Hình vuông là hình có bốn cạnh bằng nhau và bốn góc vuông.
Tính chất:
Cách vẽ:
Định nghĩa: Lục giác đều là lục giác có sáu cạnh bằng nhau và sáu góc bằng nhau.
Tính chất:
Cách vẽ:
Các hình Tam giác đều, Hình vuông và Lục giác đều xuất hiện rất nhiều trong đời sống hàng ngày. Ví dụ:
Để củng cố kiến thức về Tam giác đều, Hình vuông và Lục giác đều, các em hãy làm các bài tập sau:
Hy vọng bài học này đã giúp các em hiểu rõ hơn về Lý thuyết Tam giác đều, Hình vuông, Lục giác đều Toán 6 Cánh diều. Chúc các em học tập tốt!