Chào mừng các em học sinh đến với bài học về Lý thuyết Tập hợp Toán 6 Cánh diều. Đây là một trong những kiến thức cơ bản và quan trọng nhất trong chương trình Toán học lớp 6, đặt nền móng cho các kiến thức nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, dễ hiểu, giúp các em nắm vững khái niệm, tính chất và ứng dụng của tập hợp một cách hiệu quả.
Lý thuyết Tập hợp Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
1. Ví dụ. Kí hiệu, cách viết tập hợp. Phần tử của tập hợp
Một tập hợp ( gọi tắt là tập) bao gồm những đối tượng nhất định, những đối tượng đó được gọi là những phần tử của tập hợp mà ta nhắc đến.
Tập hợp là khái niệm cơ bản thường dùng trong toán học và cuộc sống. Ta hiểu tập hợp thông qua các ví dụ.
+ Ví dụ 1: Tập hợp các bạn nữ trong lớp 6A bao gồm tất cả các bạn nữ của lớp 6A. Đối tượng của tập hợp này là các bạn nữ của lớp 6A. Mỗi một bạn là một phần tử.
+ Ví dụ 2: Tập hợp các số nhỏ hơn \(6\)gồm tất cả các số nhỏ hơn 6, đó là 0,1,2,3,4,5. Mỗi một số trong 6 số này là một phần tử của tập hợp, chẳng hạn số 0 là một phần tử, số 1 cũng là một phần tử.
+ Hình ảnh minh họa ví dụ 2: Tập hợp các số nhỏ hơn 6 là các số trong hình quả trứng.
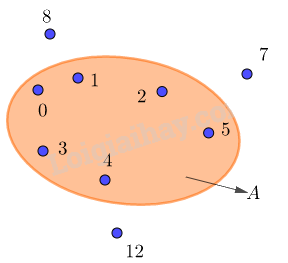
Kí hiệu:
+) Ta thường đặt tên cho tập hợp bằng các chữ cái in hoa: A, B, C, D,...
Ví dụ 2:
+) Kí hiệu tập hợp các số tự nhiên nhỏ hơn 6 là A.
Số 0 là một phần tử của A, ta kí hiệu là “\[0 \in A\]”, đọc là “0 thuộc A” hoặc “0 là phần tử của A”.
+) Số 8 không là phần tử của A, kí hiệu “\(8 \notin A\)” đọc là “8 không thuộc A” hoặc “8 không là phần tử của A”.
Cách viết tập hợp: Các phần tử của tập hợp được viết trong 2 dấu ngoặc nhọn, cách nhau bởi dấu phảy. Mỗi phần tử được liệt kê 1 lần, thứ tự tùy ý
2. Cách cho 1 tập hợp
Để viết tập hợp thường có hai cách :
Cách 1: Liệt kê các phần tử của tập hợp
Chú ý:
+ Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, ngăn cách nhau bởi dấu “ ; ” (nếu có phần tử số) hoặc dấu “ ,”
+ Mỗi phần tử được liệt kê một lần , thứ tự liệt kê tùy ý.
Ví dụ 3 : Tập hợp B gồm tất cả các số nhỏ hơn 5
Kí hiệu: \[B = \left\{ {0;1;2;3;4} \right\} = \left\{ {2;1;0;3;4} \right\}\]
Ta không được viết \[B = \left\{ {0;\underline {1;1} ;2;3;4} \right\}\] cách viết này có hai số 1 là cách viết sai.
Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó
Ví dụ 4 : \(B = \{ x|x < 5\} \)
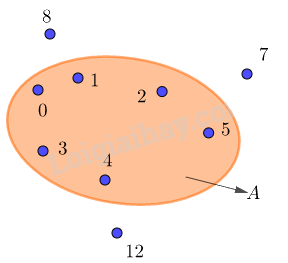
Tập hợp A trên hình vẽ \(A = \left\{ {0;1;2;3;4;5} \right\}\). Các số 1,2,3,4,5 được viết trong dấu { } và bị ngăn cách nhau bởi dấu “;”.
Tập rỗng:
Tập rỗng là tập hợp không có phần tử nào, kí hiệu \(\emptyset \).
Ví dụ lớp 6A không có bạn nào trên 100kg. Nên tập hợp các bạn trên 100kg của lớp 6A là tập rỗng.
Phương pháp:
Dùng một chữ cái in hoa và dấu ngoặc nhọn, ta có thể viết một tập hợp theo hai cách:
- Liệt kê các phần tử của nó.
- Chỉ ra tính chất đặc trưng cho các phần tử của nó
Phương pháp:
- Nắm vững ý nghĩa các kí hiệu \( \in \) và \( \notin \)
- Kí hiệu \( \in \) đọc là “phần tử của” hoặc “thuộc”.
- Kí hiệu \( \notin \) đọc là “không phải là phần tử của” hoặc ‘không thuộc”.\(\)
Phương pháp:
Sử dụng biểu đồ ven. Đó là một đường cong khép kín, không tự cắt, mỗi phần tử của tập hợp được biểu diễn bởi một điểm ở bên trong đường cong đó.
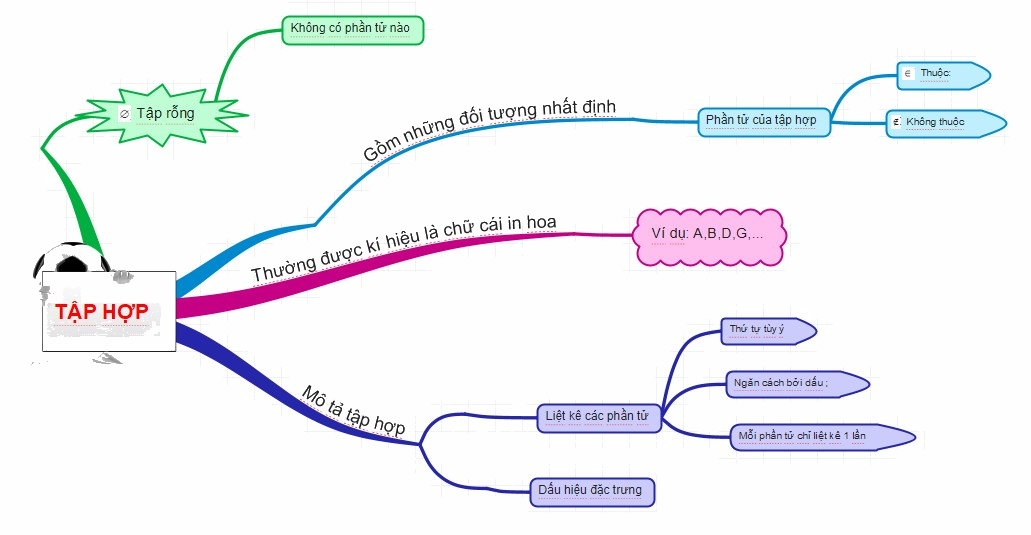
Tập hợp là một khái niệm cơ bản trong toán học, được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau. Trong chương trình Toán 6 Cánh diều, học sinh sẽ được làm quen với khái niệm tập hợp, các ký hiệu liên quan, và các phép toán cơ bản trên tập hợp.
Một tập hợp là một sưu tập các đối tượng được xác định rõ ràng. Các đối tượng này được gọi là các phần tử của tập hợp.
Có nhiều cách để biểu diễn một tập hợp:
Một số ký hiệu thường dùng trong tập hợp:
Hợp của hai tập hợp A và B là tập hợp chứa tất cả các phần tử thuộc A, thuộc B, hoặc thuộc cả A và B.
Ví dụ: A = {1, 2, 3}, B = {3, 4, 5} thì A ∪ B = {1, 2, 3, 4, 5}
Giao của hai tập hợp A và B là tập hợp chứa tất cả các phần tử thuộc cả A và B.
Ví dụ: A = {1, 2, 3}, B = {3, 4, 5} thì A ∩ B = {3}
Hiệu của hai tập hợp A và B là tập hợp chứa tất cả các phần tử thuộc A nhưng không thuộc B.
Ví dụ: A = {1, 2, 3}, B = {3, 4, 5} thì A \ B = {1, 2}
Bài 1: Cho A = {a, b, c, d} và B = {b, d, e, f}. Tìm A ∪ B, A ∩ B, A \ B, B \ A.
Bài 2: Cho tập hợp C là tập hợp các số tự nhiên lẻ nhỏ hơn 10. Hãy liệt kê các phần tử của tập hợp C.
Khái niệm tập hợp không chỉ dừng lại ở toán học mà còn được ứng dụng rộng rãi trong đời sống hàng ngày. Ví dụ, tập hợp các bạn trong lớp, tập hợp các loại trái cây, tập hợp các màu sắc,... Việc hiểu rõ về tập hợp giúp chúng ta tổ chức và phân loại thông tin một cách hiệu quả hơn.
Để nắm vững kiến thức về Lý thuyết Tập hợp Toán 6 Cánh diều, các em nên luyện tập thêm nhiều bài tập khác nhau. Các em có thể tìm thấy các bài tập này trong sách giáo khoa, sách bài tập, hoặc trên các trang web học toán online như giaitoan.edu.vn.
Lý thuyết Tập hợp Toán 6 Cánh diều là một kiến thức nền tảng quan trọng. Việc nắm vững kiến thức này sẽ giúp các em học tốt môn Toán và giải quyết các bài toán một cách dễ dàng hơn. Chúc các em học tập tốt!