Bài học này cung cấp kiến thức nền tảng về dấu hiệu chia hết cho 2 và 5, một trong những chủ đề quan trọng của chương trình Toán 6 Cánh diều. Nắm vững lý thuyết này sẽ giúp các em giải quyết các bài toán liên quan đến tính chia hết một cách nhanh chóng và chính xác.
Chúng ta sẽ cùng nhau tìm hiểu các định nghĩa, ví dụ minh họa và bài tập vận dụng để hiểu rõ hơn về dấu hiệu chia hết cho 2 và 5.
Lý thuyết Dấu hiệu chia hết cho 2, cho 5 Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
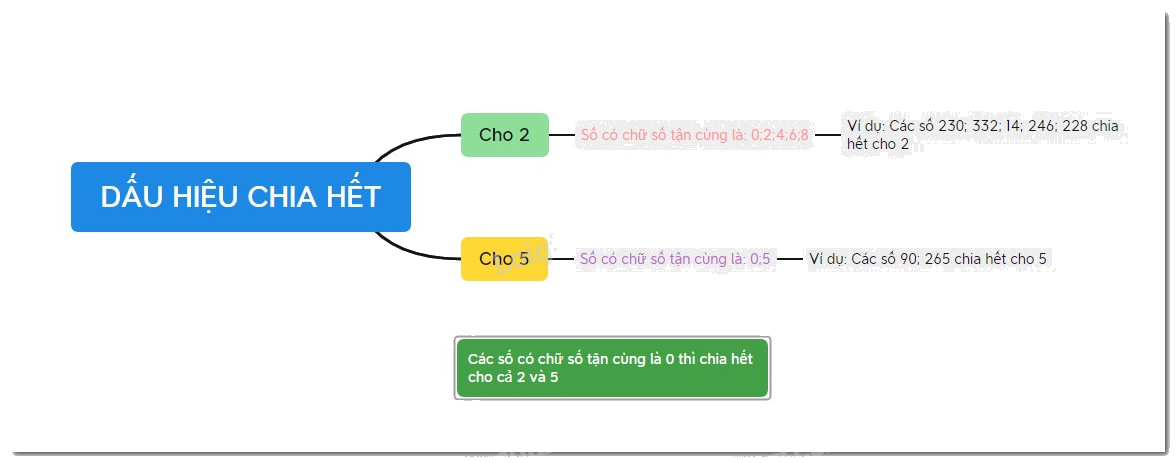
Dấu hiệu chia hết cho 2, cho 5
Chia hết cho | Dấu hiệu |
\[2\] | Chữ số tận cùng là số chẵn \(\left( {0,{\rm{ }}2,{\rm{ }}4,{\rm{ }}6,{\rm{ }}8} \right)\) |
\[5\] | Chữ số tận cùng là \(0\) hoặc \(5\) |
Ví dụ:
a) Số 15552 chia hết cho 2 vì có chữ số tận cùng là 2 và 2 là số chẵn.
b) Số 955 không chia hết cho 2 vì có chữ số tận cùng là 5 và 5 là số lẻ.
c) Số 955 và 1010 chia hết cho 5 vì có chữ số tận cùng là 5 và 0.
d) Số 1994 và 1653 không chia hết cho 5 vì có chữ số tận cùng là 4 và 3, hai số này đều khác 0 và 5.
Lưu ý: Nếu \(a\) có chữ số tận cùng là 0 thì \(a \vdots 2\), đồng thời \(a \vdots 5\)
CÁC DẠNG TOÁN VỀ DẤU HIỆU CHIA HẾT CHO 2, CHO 5
Phương pháp
Sử dụng dấu hiệu chia hết cho 2.
Sử dụng tính chất chia hết của tổng, của hiệu.
Ví dụ:
a) Các số 104, 12456, 1558 có chữ số tận cùng là số chẵn nên chia hết cho 2.
b) Các số 12345, 1234567 có chữ số tận cùng là số lẻ (5, 7) nên không chia hết cho 2.
Phương pháp
Các số chia hết cho $2$ phải có chữ số tận cùng là $0$ hoặc $2$ hoặc $4$ hoặc $6$ hoặc $8$.
Ví dụ:
Từ $3$ số $2, 3, 7$. Hãy ghép thành các số có $3$ chữ số khác nhau và chia hết cho $2$.
Giải:
Số được ghép thành chia hết cho $2$ nên phải có chữ số hàng đơn vị là $2$.
Hai chữ số hàng chục có thể là $3$ hoặc $7$.
Nếu chữ số hàng chục là $3$ thì chữ số hàng trăm là $7$. Ta được số cần tìm là $732$.
Nếu chữ số hàng chục là $7$ thì chữ số hàng trăm là $3$. Ta được số cần tìm là $372$.
Vậy có $2$ số có thể ghép thành là $372$ và $732$.
Phương pháp
Số dư trong phép chia cho 2 chỉ có thể là 0 hoặc 1.
Ví dụ:
Cho số \(N = \overline {5a} \). Tìm các số tự nhiên $N$ sao cho $N$ chia cho $2$ dư $1$.
Giải:
Ta có: \(a \in \left\{ {0;\,\,1;\,\,2;\,\,.......;\,\,9} \right\}\)
Mà $N$ chia cho $2$ dư $1$ nên $a$ chỉ có thể là $1;3;5;7;9$.
=> $N$ có thể là $51;53;55;57;59$
Phương pháp
Sử dụng dấu hiệu chia hết cho 5.
Sử dụng tính chất chia hết của tổng, của hiệu.
Ví dụ:
a) Số 12345 có chữ số tận cùng là 5 nên chia hết cho 5
b) Số 1254360 có chữ số tận cùng là 0 nên chia hết cho 5
c) Các số 5459, 34544,1498 không có chữ số tận cùng là 0 cùng không có chữ số tận cùng là 5 nên không chia hết cho 5.
Phương pháp
Các số chia hết cho $5$ phải có chữ số tận cùng là $0$ hoặc $5$.
Ví dụ:
Với $3$ số $2, 3, 5$, hãy lập các chữ số có $3$ chữ số khác nhau chia hết cho $5$.
Giải:
Số cần tìm chia hết cho 5 nên có chữ số hàng đơn vị là 5.
Chữ số hàng chục có thể là 2 hoặc 3.
Nếu chữ số hàng chục là 2 thì chữ số hàng trăm là 3. Ta được số cần tìm là 325.
Nếu chữ số hàng chục là 3 thì chữ số hàng trăm là 2. Ta được số cần tìm là 235.
Vậy có 2 số thỏa mãn bài toán là 235 và 325.
Phương pháp giải
- Số dư trong phép chia cho 5 chỉ có thể là 0, hoặc 1,hoặc 2, hoặc 3, hoặc 4.
- Mọi số tự nhiên $n$ luôn có thể được viết một trong 5 dạng sau:
+) Dạng 1: $n=5k$ (số chia hết cho 5);
+) Dạng 2: $n=5k+1$ (số chia cho 5 dư 1);
+) Dạng 3: $n=5k+2$ (số chia cho 5 dư 2);
+) Dạng 3: $n=5k+3$ (số chia cho 5 dư 3);
+) Dạng 3: $n=5k+4$ (số chia cho 5 dư 4).
Với $k\in \mathbb{Z}$.
Ví dụ:
Cho số \(N = \overline {5a} \). Tìm các số tự nhiên $N$ sao cho $N$ chia cho $5$ dư $1$.
Giải:
Vì $N$ chia cho $5$ dư $1$ mà \(a \in \left\{ {0;\,\,1;\,\,2;\,\,.......;\,\,9} \right\}\) nên $a$ chỉ có thể là $1$ hoặc $6$.
=> $N$ có thể là $51;56$.
Trong chương trình Toán 6, việc nắm vững các dấu hiệu chia hết là vô cùng quan trọng. Nó không chỉ giúp học sinh giải quyết các bài toán một cách nhanh chóng mà còn là nền tảng cho các kiến thức toán học nâng cao hơn. Bài viết này sẽ đi sâu vào lý thuyết dấu hiệu chia hết cho 2 và 5, theo chương trình Cánh diều.
Một số nguyên được gọi là chia hết cho 2 nếu chữ số tận cùng của nó là 0, 2, 4, 6 hoặc 8. Nói cách khác, số đó là một số chẵn.
Một số nguyên được gọi là chia hết cho 5 nếu chữ số tận cùng của nó là 0 hoặc 5.
Dấu hiệu chia hết cho 2 và 5 thường được sử dụng để kiểm tra xem một số có chia hết cho 2 hoặc 5 hay không, hoặc để tìm các số chia hết cho 2 hoặc 5 trong một khoảng cho trước.
Bài tập 1: Số nào sau đây chia hết cho 2?
Giải: Số 24 chia hết cho 2 vì chữ số tận cùng là 4.
Bài tập 2: Số nào sau đây chia hết cho 5?
Giải: Số 25 chia hết cho 5 vì chữ số tận cùng là 5.
Đôi khi, chúng ta cần kết hợp các dấu hiệu chia hết để xác định một số có chia hết cho nhiều số hay không. Ví dụ, một số chia hết cho cả 2 và 5 thì phải chia hết cho 10 (vì 2 x 5 = 10).
Bài tập 3: Số nào sau đây chia hết cho 10?
Giải: Số 20 chia hết cho 10 vì chữ số tận cùng là 0.
Để nắm vững hơn về dấu hiệu chia hết cho 2 và 5, các em nên luyện tập thêm nhiều bài tập khác nhau. Các em có thể tìm thấy các bài tập này trong sách giáo khoa, sách bài tập hoặc trên các trang web học toán online như giaitoan.edu.vn.
Bảng tổng hợp dấu hiệu chia hết cho 2 và 5:
| Dấu hiệu | Điều kiện |
|---|---|
| Chia hết cho 2 | Chữ số tận cùng là 0, 2, 4, 6, 8 |
| Chia hết cho 5 | Chữ số tận cùng là 0 hoặc 5 |
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về lý thuyết dấu hiệu chia hết cho 2 và 5 Toán 6 Cánh diều. Chúc các em học tốt!