Chào mừng các em học sinh đến với bài học về Lý thuyết Tỉ số. Tỉ số phần trăm trong chương trình Toán 6 Cánh diều. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về tỉ số và tỉ số phần trăm, giúp các em giải quyết các bài toán thực tế một cách dễ dàng.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, cách tính tỉ số, tỉ số phần trăm, và các ứng dụng của chúng trong cuộc sống hàng ngày. Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Lý thuyết Tỉ số. Tỉ số phần trăm Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
I. Tỉ số
a) Tỉ số của hai số
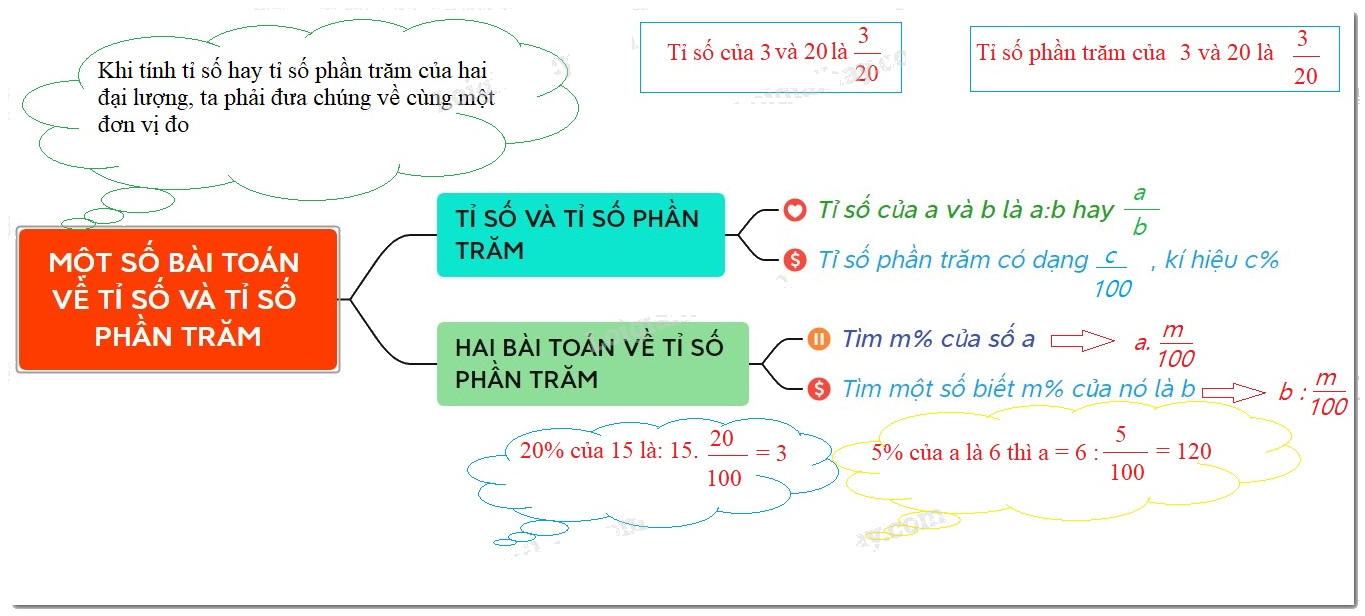
Tỉ số của hai số $ a$ và $ b$ tùy ý $ \left( {b \ne 0} \right)$ là thương của phép chia số $ a$ cho số $ b$ . Kí hiệu là $ a:b$ hoặc $ \dfrac{a}{b}$ .
Chú ý: Nếu tỉ số của $ a$ và $ b$ được viết dưới dạng $ \dfrac{a}{b}$ thì ta cũng gọi $ a$ là tử số và $ b$ là mẫu số.
Ví dụ:
Tỉ số của $ - 5$ và $ 7$ là: $ \dfrac{{ - 5}}{7}$ .
b) Tỉ số của hai đại lượng
Tỉ số của hai đại lượng cùng loại và cùng đơn vị đo là tỉ số giữa hai số đo của hai đại lượng đó.
Nhận xét:
Tỉ số của hai đại lượng thể hiện độ lớn của đại lượng này so với đại lượng kia.
Chú ý:
- Phân số $ \dfrac{a}{b}$ thì cả $ a$ và $ b$ phải là các số nguyên.
- Tỉ số $ \dfrac{a}{b}$ thì $ a$ và $ b$ có thể là các số nguyên, phân số, hỗn số, số thập phân,…
Ví dụ:
Tỉ số chiều dài hai đoạn thẳng $ AB = 1,5\,\,\,cm$ và $ CD = \dfrac{1}{3}\,cm$ là: $ 1,5:\dfrac{1}{3}$ .
Tỉ số phần trăm của a và b là $ \dfrac{a}{b}.100\% $ .
Ví dụ:
a) Tỉ số phần trăm của $ 3$ và $ 6$ là:
$ \dfrac{{3.100}}{6}\% = \dfrac{{300}}{6}\% = 50\% .$
b) Tỉ số phần trăm của $ - 2,3$ và $ 10$ là: $ \dfrac{{ - 2,3.100}}{{10}}\% = - 23\% $
Chú ý: Tỉ số $ \dfrac{{a.100}}{b}$ không nhất thiết là số nguyên.
Để tính tỉ số của hai số ta tính $ a:b$ hoặc $ \dfrac{a}{b}$ $ \left( {b \ne 0} \right)$
Để tính tỉ số phần trăm của a và b, ta làm như sau:
Bước 1. Viết tỉ số $ \dfrac{a}{b}$
Bước 2. Tính số $ \dfrac{{a.100}}{b}$ và viết thêm % vào bên phải số vừa nhận được.
- Viết một số a dưới dạng dùng kí hiệu %: \(a = \dfrac{{a.100}}{{100}} = (100.a)\% \)
- Viết \(a\% \) dưới dạng phân số: \(a\% = \dfrac{a}{{100}}\)
- Đổi số thập phân ra phân số: \(\overline {a,bc} = \dfrac{{\overline {abc} }}{{100}} = \overline {abc} \% ;\,\,\,\,\,\overline {a,{b_1}{b_2}...{b_n}} = \dfrac{{a{b_1}{b_2}...{b_n}}}{{{{10}^n}}}\)
- Một phân số tối giản có mẫu số chỉ có ước số nguyên tố là 2 hoặc 5 thì có thể viết dưới dạng số thập phân (hữu hạn).
Trong chương trình Toán 6, kiến thức về tỉ số và tỉ số phần trăm đóng vai trò nền tảng cho việc hiểu và giải quyết các bài toán liên quan đến số học và đại số. Bài viết này sẽ trình bày chi tiết lý thuyết, ví dụ minh họa và bài tập thực hành để giúp học sinh nắm vững kiến thức này.
Tỉ số của hai số a và b (với b ≠ 0) là thương của phép chia a cho b, được viết là a : b hoặc a/b. Tỉ số cho ta biết mức độ so sánh giữa hai đại lượng. Ví dụ, nếu chiều cao của An là 160cm và chiều cao của Bình là 170cm, thì tỉ số chiều cao của An so với Bình là 160/170 = 16/17.
Tỉ số phần trăm là một cách biểu diễn tỉ số dưới dạng phần trăm. Để chuyển một tỉ số a/b thành tỉ số phần trăm, ta nhân tỉ số đó với 100%. Ví dụ, tỉ số 16/17 khi chuyển thành tỉ số phần trăm là (16/17) * 100% ≈ 94.12%.
Để tính tỉ số phần trăm của một số a so với một số b, ta thực hiện các bước sau:
Ví dụ: Tính tỉ số phần trăm của 20 so với 80.
Tỉ số và tỉ số phần trăm được ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống:
Bài 1: Một lớp học có 30 học sinh, trong đó có 12 học sinh giỏi. Tính tỉ số phần trăm học sinh giỏi của lớp.
Giải:
Bài 2: Một cửa hàng giảm giá 10% cho một chiếc áo sơ mi có giá gốc là 200.000 đồng. Hỏi giá chiếc áo sau khi giảm giá là bao nhiêu?
Giải:
Khi tính tỉ số phần trăm, cần chú ý đến đơn vị của các đại lượng. Nếu các đại lượng có đơn vị khác nhau, cần phải quy đổi về cùng một đơn vị trước khi tính tỉ số.
Hi vọng bài viết này đã giúp các em hiểu rõ hơn về lý thuyết tỉ số và tỉ số phần trăm trong chương trình Toán 6 Cánh diều. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải quyết các bài toán thực tế. Chúc các em học tốt!