Bài học này cung cấp kiến thức nền tảng về cách so sánh phân số và hỗn số dương, một chủ đề quan trọng trong chương trình Toán 6 Cánh diều. Chúng tôi sẽ trình bày lý thuyết một cách dễ hiểu, kèm theo các ví dụ minh họa cụ thể.
Học sinh sẽ được làm quen với các phương pháp so sánh phân số khác nhau, từ việc quy đồng mẫu số đến việc sử dụng tính chất của phân số. Ngoài ra, bài học cũng sẽ hướng dẫn cách chuyển đổi hỗn số thành phân số và ngược lại, giúp học sinh tự tin giải quyết các bài toán liên quan.
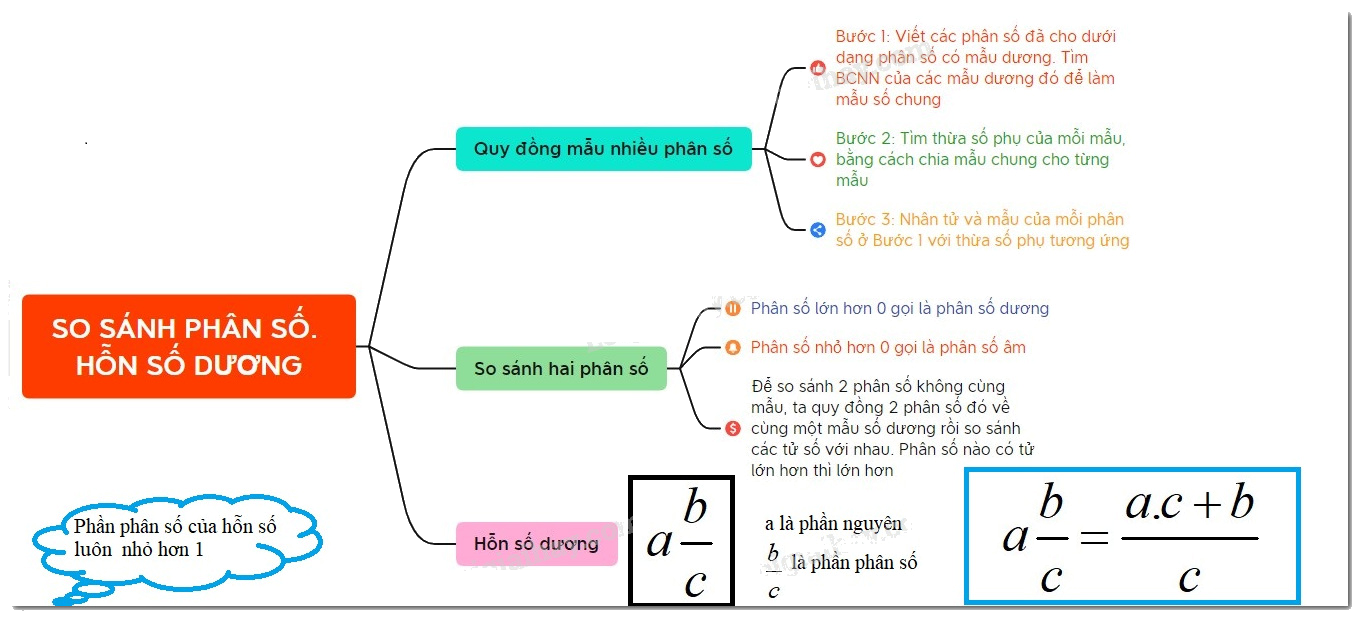
Lý thuyết So sánh phân số. Hỗn số dương Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
1. So sánh các phân số:
Trong 2 phân số khác nhau luôn có một phân số lớn hơn phân số kia
*Phân số lớn hơn 0 gọi là phân số dương
*Phân số nhỏ hơn 0 gọi là phân số âm
*Nếu phân số \(\frac{a}{b}\) nhỏ hơn phân số \(\frac{c}{d}\) thì ta viết \(\frac{a}{b}< \frac{c}{d}\) hay \(\frac{c}{d}> \frac{a}{b}\)
*Nếu \(\frac{a}{b}< \frac{c}{d}\) và \(\frac{c}{d}< \frac{e}{g}\) thì \(\frac{a}{b}< \frac{e}{g}\)
Trong hai phân số có cùng một mẫu dương, phân số nào có tử lớn hơn thì lớn hơn.
Ví dụ: So sánh $\dfrac{{ - 4}}{5}$ và $\dfrac{{ - 7}}{5}$.
Ta có: $ - 4 > - 7$ và $5 > 0$ nên $\dfrac{{ - 4}}{5} > \dfrac{{ - 7}}{5}$.
Chú ý: Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh.
Ví dụ:
So sánh $\dfrac{{ - 4}}{{ - 5}}$ và $\dfrac{2}{{ - 5}}$
Đưa hai phân số trên về có cùng một mẫu nguyên âm: $\dfrac{4}{5}$ và $\dfrac{{ - 2}}{5}$
Ta có: $4 > - 2$ và $5 > 0$ nên $\dfrac{4}{5} > \dfrac{{ - 2}}{5}$.
Bước 1: Quy đồng mẫu hai phân số đã cho (về cùng một mẫu dương)
Bước 2: So sánh tử của các phân số: Phân số nào có tử lớn hơn thì lớn hơn.
Ví dụ: So sánh hai phân số $\dfrac{{ - 7}}{{12}}$ và $\dfrac{{ - 11}}{{18}}$.
$BCNN(12;18) = 36$ nên ta có:
$\dfrac{{ - 7}}{{12}} = \dfrac{{ - 7.3}}{{12.3}} = \dfrac{{ - 21}}{{36}}$
$\dfrac{{ - 11}}{{18}} = \dfrac{{ - 11.2}}{{18.2}} = \dfrac{{ - 22}}{{36}}$.
Vì $ - 21 > - 22$ nên $\dfrac{{ - 21}}{{36}} > \dfrac{{ - 22}}{{36}}$. Do đó $\dfrac{{ - 7}}{{12}} > \dfrac{{ - 11}}{{18}}$.
Phân số có tử và mẫu là hai số nguyên cùng dấu thì lớn hơn $0$, gọi là phân số dương.
Ví dụ:$\dfrac{{ - 3}}{{ - 5}} > 0$ hoặc $\dfrac{4}{5} > 0$
Phân số có tử và mẫu là hai số nguyên khác dấu thì nhỏ hơn $0$, gọi là phân số âm.
Ví dụ : $\dfrac{{ - 3}}{5} < 0$
- Ta còn có các cách so sánh phân số như sau:
+ Áp dụng tính chất: $\dfrac{a}{b} < \dfrac{c}{d} \Leftrightarrow a.d < b.c{\rm{\;}}({\rm{a}},{\rm{b}},{\rm{c}},{\rm{d}} \in {\rm{Z}};{\rm{b}},{\rm{d\;}} > {\rm{\;0}})$
+ Đưa về hai phân số cùng tử dương rồi so sánh mẫu (chỉ áp dụng đối với hai phân số cùng âm hoặc cùng dương)
Ví dụ: $\dfrac{4}{{ - 9}} > \dfrac{4}{{ - 7}};$$\dfrac{3}{5} < \dfrac{3}{2}$
+ Chọn số thứ ba làm trung gian.
Ví dụ:
$\dfrac{{ - 4}}{9} < 0 < \dfrac{4}{7}{\kern 1pt}$ suy ra $\dfrac{{ - 4}}{9}<\dfrac{4}{7}$
$\dfrac{{14}}{9} > 1 > \dfrac{4}{7}$ suy ra $\dfrac{{14}}{9}>\dfrac{4}{7}$
+ Sử dụng tính chất so sánh: Nếu \(\dfrac{a}{b} < 1\) thì \(\dfrac{a}{b} < \dfrac{{a + m}}{{b + m}}\)
2. Hỗn số dương
Viết một phân số lớn hơn 1 thành tổng của một số nguyên dương và một phân số nhỏ hơn 1 ( với tử và mẫu dương) rồi viết chúng liền nhau thì được 1 hỗn số dương.
Ví dụ:
\(\frac{7}{4}= \frac{4.1+3}{4}= 1 + \frac{3}{4}=1\frac{3}{4}\)
Trong chương trình Toán 6, việc nắm vững kiến thức về phân số là vô cùng quan trọng. Một trong những chủ đề then chốt là so sánh phân số và làm việc với hỗn số dương. Bài viết này sẽ cung cấp một cái nhìn toàn diện về lý thuyết này, được thiết kế đặc biệt cho học sinh theo chương trình Cánh diều.
Phân số là biểu thức của một phần của một đơn vị. Một phân số được viết dưới dạng a/b, trong đó a là tử số (số phần được lấy) và b là mẫu số (tổng số phần bằng nhau).
Có nhiều cách để so sánh phân số:
Hỗn số là một số được viết dưới dạng tổng của một số nguyên và một phân số. Ví dụ: 2 1/3 là một hỗn số.
Để chuyển đổi một hỗn số a b/c thành phân số, ta thực hiện phép tính: (a * c + b) / c
Ví dụ: 2 1/3 = (2 * 3 + 1) / 3 = 7/3
Để chuyển đổi một phân số a/b thành hỗn số, ta thực hiện phép chia a cho b. Thương là phần nguyên của hỗn số, số dư là tử số của phân số trong hỗn số, và mẫu số vẫn là b.
Ví dụ: 7/3 = 2 dư 1, vậy 7/3 = 2 1/3
Để so sánh hai hỗn số, ta có thể:
Ví dụ 1: So sánh 2/5 và 3/5.
Vì hai phân số có cùng mẫu số, ta so sánh tử số: 2 < 3. Vậy 2/5 < 3/5.
Ví dụ 2: So sánh 1 1/2 và 2 1/3.
Chuyển đổi hỗn số thành phân số: 1 1/2 = 3/2 và 2 1/3 = 7/3.
Quy đồng mẫu số: 3/2 = 9/6 và 7/3 = 14/6.
So sánh tử số: 9 < 14. Vậy 3/2 < 7/3 hay 1 1/2 < 2 1/3.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết so sánh phân số và hỗn số dương Toán 6 Cánh diều. Chúc bạn học tập tốt!