Bài học này cung cấp kiến thức nền tảng về hai loại quan hệ giữa các đường thẳng: cắt nhau và song song. Nội dung được trình bày theo chương trình Toán 6 Cánh diều, giúp học sinh dễ dàng tiếp thu và áp dụng vào giải bài tập.
Chúng ta sẽ cùng tìm hiểu các định nghĩa, tính chất và cách nhận biết hai đường thẳng cắt nhau và song song. Đặc biệt, bài học sẽ tập trung vào việc vận dụng lý thuyết vào các bài toán thực tế.
Lý thuyết Hai đường thẳng cắt nhau. Hai đường thẳng song song Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
1. Hai đường thẳng cắt nhau
Nếu hai đường thẳng chỉ có một điểm chung, ta nói rằng hai đường thẳng đó cắt nhau. Điểm chung được gọi là giao điểm của hai đường thẳng.
Ví dụ:
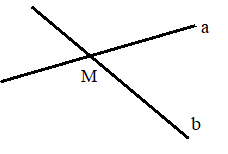
2 đường thẳng a và b cắt nhau. Điểm M được gọi là giao điểm của 2 đường thẳng a và b.
Người ta còn nói: 2 đường thẳng a và b cắt nhau tại M
2. Hai đường thẳng song song
Nếu hai đường thẳng không có điểm chung nào, ta nói rằng hai đường thẳng đó song song với nhau. Ta viết a//b hay b//a
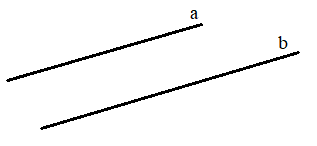
Chú ý: Từ nay về sau, khi nói hai đường thẳng mà không nói gì thêm, ta hiểu đó là hai đường thẳng phân biệt.
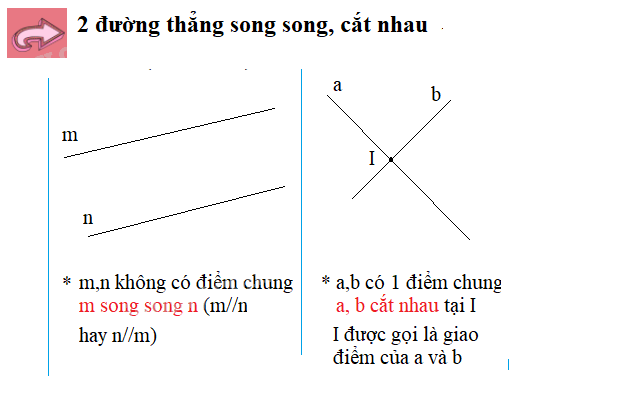
Trong hình học, việc hiểu rõ mối quan hệ giữa các đường thẳng là vô cùng quan trọng. Bài viết này sẽ đi sâu vào lý thuyết về hai đường thẳng cắt nhau và hai đường thẳng song song, được trình bày theo chương trình Toán 6 Cánh diều.
Hai đường thẳng được gọi là cắt nhau nếu chúng có một điểm chung duy nhất. Điểm chung này được gọi là giao điểm của hai đường thẳng. Khi hai đường thẳng cắt nhau, chúng tạo thành bốn góc. Hai góc đối đỉnh thì bằng nhau.
Hai đường thẳng được gọi là song song nếu chúng không có điểm chung nào. Điều này có nghĩa là chúng không bao giờ gặp nhau, dù kéo dài vô hạn.
Để nhận biết hai đường thẳng cắt nhau, ta cần tìm xem chúng có điểm chung hay không. Nếu có, chúng cắt nhau. Để nhận biết hai đường thẳng song song, ta cần chứng minh rằng chúng không có điểm chung.
Có một số cách để chứng minh hai đường thẳng song song:
Ví dụ 1: Cho hai đường thẳng a và b cắt nhau tại điểm O. Biết góc AOB = 60 độ. Tính góc đối đỉnh với góc AOB.
Giải: Vì góc AOB và góc đối đỉnh của nó bằng nhau, nên góc đối đỉnh với góc AOB cũng bằng 60 độ.
Ví dụ 2: Cho hai đường thẳng c và d song song với nhau. Một đường thẳng t cắt hai đường thẳng c và d lần lượt tại A và B. Biết góc cAt = 80 độ. Tính góc dBt.
Giải: Vì c // d và t cắt c và d, nên góc cAt và góc dBt là hai góc so le trong. Do đó, góc dBt = góc cAt = 80 độ.
1. Cho hai đường thẳng m và n cắt nhau tại điểm I. Biết góc MIN = 45 độ. Tính các góc còn lại tại điểm I.
2. Cho hai đường thẳng p và q song song với nhau. Một đường thẳng k cắt hai đường thẳng p và q lần lượt tại C và D. Biết góc pCk = 120 độ. Tính góc qCd.
3. Vẽ hai đường thẳng a và b cắt nhau tại điểm O. Vẽ đường thẳng c cắt a tại A và b tại B. Nêu các cặp góc đối đỉnh và các cặp góc so le trong.
Lý thuyết về hai đường thẳng cắt nhau và hai đường thẳng song song là nền tảng quan trọng trong hình học. Việc nắm vững các định nghĩa, tính chất và cách nhận biết sẽ giúp học sinh giải quyết các bài toán một cách hiệu quả. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán.
| Khái niệm | Định nghĩa |
|---|---|
| Đường thẳng cắt nhau | Hai đường thẳng có một điểm chung. |
| Đường thẳng song song | Hai đường thẳng không có điểm chung. |