Chào mừng các em học sinh đến với bài học về Lý thuyết Hình thang cân Toán 6 Cánh diều tại giaitoan.edu.vn. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về hình thang cân, giúp các em tự tin giải các bài tập liên quan.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất, dấu hiệu nhận biết hình thang cân, cũng như các ứng dụng thực tế của kiến thức này trong môn Toán.
Lý thuyết Hình thang cân Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
1. Nhận biết hình thang cân
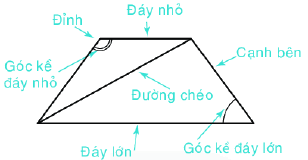
- Hai cạnh bên bằng nhau.
- Hai đường chéo bằng nhau
- Hai đáy song song với nhau
- Hai góc kề một đáy bằng nhau.
2. Chu vi và diện tích hình thang cân
Chu vi hình thang bằng tổng độ dài các cạnh của nó
Diện tích hình thang bằng tổng độ dài 2 đáy nhân với chiều cao rồi chia 2
Hình thang cân là một trong những hình quan trọng trong chương trình Hình học lớp 6. Việc nắm vững lý thuyết về hình thang cân là nền tảng để giải quyết các bài toán phức tạp hơn trong tương lai. Bài viết này sẽ trình bày chi tiết lý thuyết về hình thang cân theo chương trình Toán 6 Cánh diều, giúp các em học sinh hiểu rõ và áp dụng hiệu quả.
Hình thang cân là hình thang có hai cạnh bên song song. Nói cách khác, một tứ giác là hình thang cân khi và chỉ khi nó là hình thang và hai cạnh bên bằng nhau.
Ví dụ: Tứ giác ABCD là hình thang cân nếu AB // CD và AD = BC.
Hình thang cân có những tính chất quan trọng sau:
Chứng minh tính chất:
Để chứng minh các tính chất trên, ta thường sử dụng các tam giác bằng nhau. Ví dụ, để chứng minh ∠A = ∠D, ta có thể chứng minh tam giác ADH bằng tam giác BCK (cạnh huyền - góc nhọn).
Có những dấu hiệu sau để nhận biết một hình thang cân:
Ví dụ: Nếu trong hình thang ABCD có ∠A = ∠D thì ABCD là hình thang cân.
Lý thuyết về hình thang cân được ứng dụng trong nhiều bài toán thực tế, ví dụ như:
Bài 1: Cho hình thang cân ABCD (AB // CD, AB < CD). Biết ∠A = 80°. Tính ∠B, ∠C, ∠D.
Giải:
Vì ABCD là hình thang cân nên ∠A = ∠D = 80° và ∠B = ∠C.
Ta có ∠A + ∠B = 180° (hai góc kề một cạnh bên của hình thang)
=> ∠B = 180° - ∠A = 180° - 80° = 100°
Vậy ∠B = ∠C = 100° và ∠D = 80°.
Bài 2: Cho hình thang cân ABCD (AB // CD). Gọi M là giao điểm của hai đường chéo AC và BD. Chứng minh rằng tam giác MCD cân tại M.
Giải:
Vì ABCD là hình thang cân nên AC = BD.
Xét tam giác MCD có MC = MD (vì AC = BD và M là giao điểm của AC và BD).
=> Tam giác MCD cân tại M.
Để học tốt lý thuyết về hình thang cân, các em cần:
Hy vọng bài viết này đã cung cấp cho các em những kiến thức hữu ích về Lý thuyết Hình thang cân Toán 6 Cánh diều. Chúc các em học tập tốt!
| Khái niệm | Mô tả |
|---|---|
| Hình thang | Tứ giác có hai cạnh đối song song. |
| Hình thang cân | Hình thang có hai cạnh bên song song. |