Chào mừng các em học sinh đến với bài học về Lý thuyết Số nguyên tố và Hợp số trong chương trình Toán 6 Cánh diều. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về các khái niệm này.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất của số nguyên tố, hợp số, cách nhận biết và ứng dụng của chúng trong giải toán. Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
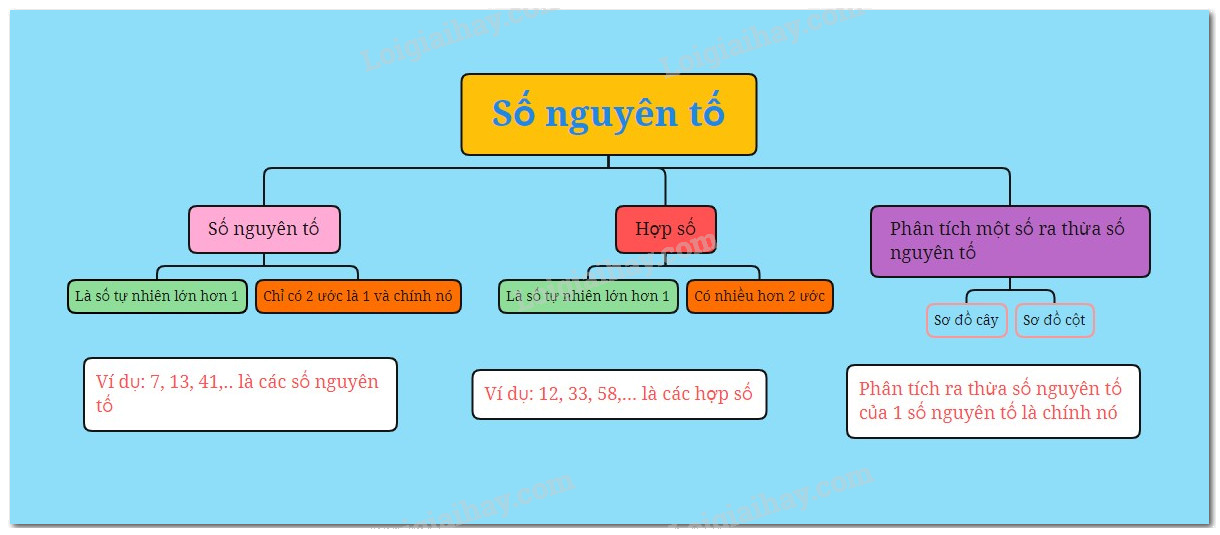
Lý thuyết Số nguyên tố. Hợp số Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
I. Số nguyên tố và hợp số
1. Số nguyên tố
- Số nguyên tố là số tự nhiên lớn hơn \(1,\)chỉ có \(2\)ước là \(1\) và chính nó.
Ví dụ : Ư\((13) = \{ 13;1\} \) nên \(13\) là số nguyên tố.
Cách kiểm tra 1 số là số nguyên tố:
Để kết luận số a là số nguyên tố \(\left( {a > 1} \right),\)ta làm như sau:
Bước 1: Tìm số nguyên tố lớn nhất \(b\) mà \({b^2} < a\).
Bước 2: Lấy \(a\) chia cho các số nguyên tố từ 2 đến số nguyên tố \(b\), nếu \(a\) không chia hết cho số nào thì \(a\) là số nguyên tố.
2. Hợp số
Hợp số là số tự nhiên lớn hơn \(1,\) có nhiều hơn \(2\) ước.
Ví dụ: số \(15\) có \(4\) ước là \(1;3;5;15\) nên \(15\) là hợp số.
Lưu ý:
+) Số 0 và số 1 không là số nguyên tố cũng không là hợp số.
+) Kiểm tra một số \(a\) là hợp số: Sử dụng dấu hiệu chia hết để tìm một ước của \(a\) khác 1 và \(a\).
1. Cách tìm một ước nguyên tố của một số
Để tìm một ước nguyên tố của \(a\) ta có thể làm như sau:
Bước 1: Chia \(a\) cho các số nguyên tố theo thứ tự tăng dần \(2,3,5,7,11,13,...\)
Bước 2: Số chia trong phép chia hết đầu tiên là một ước của \(a\)
Ví dụ:
Tìm ước nguyên tố của 91:
Theo các dấu hiệu chia hết cho 2, 3 và 5 thì 91 không chia hết cho 2 , cho 3 và cho 5.
Ta chia 91 cho số nguyên tố tiếp theo:
Ta lấy 91:7=13. Vì thế 7 là một ước nguyên tố của 91.
2. Phân tích một số ra thừa số nguyên tố
- Phân tích một số tự nhiên lớn hơn \(1\) ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
- Viết các thừa số nguyên tố theo thứ tự từ bé đến lớn, tích các thừa số giống nhau dưới dạng lũy thừa.
Sơ đồ cây:
Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.
Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.
Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.
Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.
Sơ đồ cột:
Chia số \(n\) cho một số nguyên tố (xét từ nhỏ đến lớn ), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng \(1.\)
Ví dụ: Số \(76\) được phân tích như sau:
\(76\) | \(2\) |
\(38\) | \(2\) |
\(19\) | \(19\) |
\(1\) |
Như vậy \(76 = {2^2}.19\)
Phương pháp:
+ Căn cứ vào định nghĩa số nguyên tố và hợp số.
+ Căn cứ vào các dấu hiệu chia hết.
+ Có thể dùng bảng số nguyên tố để xác định một số (nhỏ hơn 1000) là số nguyên tố hay không.
Ví dụ:
Tìm các số * để được số nguyên tố $\overline {*1} $:
Dấu * có thể nhận các giá trị \(\left\{ {1;2;3;4;5;6;7;8;9} \right\}\)
+) Với $a=1$ ta có \(11\) là số nguyên tố => Thỏa mãn.
+) Với $a=2$ ta có \(21\) có các ước \(1;3;7;21\) nên \(21\) là hợp số=> Loại.
+) Với $a=3$ ta có \(31\) là số nguyên tố => Thỏa mãn.
+) Với $a=4$ ta có \(41\) chỉ có hai ước là \(1;41\) nên \(41\) là số nguyên tố => Thỏa mãn.
+) Với $a=5$ ta có \(51\) có các ước \(1;3;17;51\) nên \(51\) là hợp số. Loại
+) Với $a=6$ ta có \(61\) là số nguyên tố => Thỏa mãn.
+) Với $a=7$ ta có \(71\) là số nguyên tố => Thỏa mãn.
+) Với $a=8$ ta có \(81\) có các ước \(1;3;9;27;81\) nên \(81\) là hợp số. Loại.
+) Với $a=9$ ta có \(91\) là có các ước \(1;7;13;91\) nên \(91\) là hợp số. Loại
Vậy các số nguyên tố là: $11,31,41,61,71$.
Phương pháp:
+ Để chứng minh một số là số nguyên tố, ta chứng minh số đó không có ước nào khác $1$ và chính nó.
+ Để chững minh một số là hợp số, ta chỉ ra rằng tồn tại một ước của nó khác $1$ và khác chính nó. Nói cách khác, ta chứng minh số đó có nhiều hơn hai ước.
Ví dụ:
a) $5$ là số nguyên tố vì nó chỉ có hai ước là $1$ và $5$.
b) $12$ là hợp số vì nó có nhiều hơn hai ước. Cụ thể 12 có các ước là: $1; 2; 3; 4; 6; 12$
Trong chương trình Toán 6, việc nắm vững kiến thức về số nguyên tố và hợp số là vô cùng quan trọng. Đây là nền tảng để học sinh hiểu sâu hơn về các khái niệm toán học phức tạp hơn ở các lớp trên. Bài viết này sẽ cung cấp một cách chi tiết và dễ hiểu về lý thuyết này, kèm theo các ví dụ minh họa và bài tập thực hành.
Trước khi đi vào lý thuyết về số nguyên tố và hợp số, chúng ta cần ôn lại khái niệm về số tự nhiên. Số tự nhiên là các số dùng để đếm, bao gồm 0, 1, 2, 3,... Tập hợp các số tự nhiên được ký hiệu là ℕ.
Một số tự nhiên lớn hơn 1 được gọi là số nguyên tố nếu chỉ chia hết cho 1 và chính nó. Ví dụ: 2, 3, 5, 7, 11, 13,...
Một số tự nhiên lớn hơn 1 được gọi là hợp số nếu có ít nhất ba ước số khác nhau. Ví dụ: 4, 6, 8, 9, 10,...
Số 1 không phải là số nguyên tố cũng không phải là hợp số. Nó là một trường hợp đặc biệt.
Để nhận biết một số là nguyên tố hay hợp số, ta có thể sử dụng các phương pháp sau:
Số nguyên tố và hợp số có nhiều ứng dụng trong toán học và thực tế, bao gồm:
Bài 1: Điền vào chỗ trống:
Bài 2: Cho các số sau: 2, 4, 5, 6, 7, 9, 11, 12. Hãy chia các số này thành hai nhóm: số nguyên tố và số hợp số.
Bài 3: Phân tích các số sau ra thừa số nguyên tố: 18, 24, 30.
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về Lý thuyết Số nguyên tố và Hợp số Toán 6 Cánh diều. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải các bài tập thực tế. Chúc các em học tốt!