Bài học này cung cấp kiến thức nền tảng về quan hệ chia hết và các tính chất quan trọng của nó trong chương trình Toán 6 Cánh diều. Học sinh sẽ được làm quen với khái niệm chia hết, số chia hết, và cách xác định một số có chia hết cho một số khác hay không.
Chúng tôi sẽ trình bày lý thuyết một cách dễ hiểu, kèm theo các ví dụ minh họa cụ thể để giúp học sinh nắm bắt kiến thức một cách nhanh chóng và hiệu quả.
Lý thuyết Quan hệ chia hết. Tính chất chia hết Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
I. Quan hệ chia hết
1. Khái niệm về chia hết
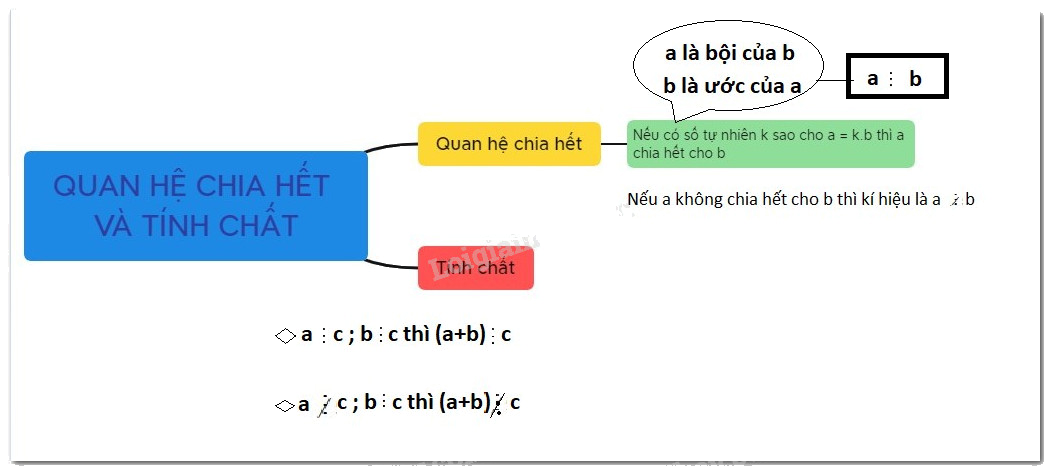
Cho hai số tự nhiên \(a\) và \(b,\) trong đó \(b \ne 0,\) nếu có số tự nhiên \(x\) sao cho \(b.x = a\) thì ta nói \(a\) chia hết cho \(b\) và ta có phép chia hết \(a:b = x\)
Nếu \(a\) không chia hết cho \(b,\) ta kí hiệu là \(a\not \vdots b\).
Ước và bội
- Nếu có số tự nhiên \(a\) chia hết cho số tự nhiên \(b\) thì ta nói \(a\) là bội của \(b,\) còn \(b\) là ước của \(a.\)
- Kí hiệu: Ư\(\left( a \right)\) là tập hợp các ước của \(a\) và \(B\left( b \right)\) là tập hợp các bội của \(b\).
Ví dụ : \(12 \vdots 6 \Rightarrow 12\) là bội của \(6.\) Còn \(6\) được gọi là ước của \(12\)
2. Cách tìm ước và bội
Tìm ước:
- Ta có thể tìm các ước của \(a\)\(\left( {a > 1} \right)\) bằng cách lần lượt chia \(a\) cho các số tự nhiên từ \(1\) đến \(a\) để xét xem \(a\) chia hết cho những số nào, khi đó các số ấy là ước của \(a.\)
Ví dụ :
16:1=16; 16:2=8; 16:4=4; 16:8=2; 16:16=1
Vậy các ước của 16 là 1;2;4;8;16. Tập hợp các ước của 16 là:
Ư\(\left( {16} \right) = \left\{ {1;2;4;8;16} \right\}\)
Tìm bội:
- Ta có thể tìm các bội của một số khác \(0\) bằng cách nhân số đó lần lượt với \(0,1,2,3,...\)
Ví dụ :
Ta lấy 6 nhân với từng số 0 thì được 0 nên 0 là bội của 6, lấy 6.1=6 nên 6 là bội của 6, 6.2=12 nên 12 là bội của 6,...
Vậy \(B\left( 6 \right) = \left\{ {0;6;12;18;...} \right\}\)
II. Tính chất chia hết
1. Tính chất chia hết của một tổng
- Tính chất: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.
\(a \vdots m\) và \(b \vdots m\) \( \Rightarrow \left( {a + b} \right) \vdots m\)
\(a\, \vdots \,m;\,b \vdots m;\,c \vdots m \Rightarrow \left( {a + b + c} \right) \vdots m\)
Chú ý: Nếu chỉ có một số hạng của tổng không chia hết cho một số, còn các số hạng khác đều chia hết cho số đó thì tổng không chia hết cho số đó.
\(a \vdots m\) và \(b\not \vdots m\)\( \Rightarrow \left( {a + b} \right)\not \vdots m\)
\(a\not \vdots m;\,b \vdots m;\,c \vdots m \Rightarrow \left( {a + b + c} \right)\not \vdots m\)
Ví dụ: Ta có \(6 \vdots 3;\,9 \vdots 3;\,15 \vdots 3\, \Rightarrow 6 + 9 + 15 = 30 \vdots 3\);\(10 \vdots 5;\,15 \vdots 5;\,12\not \vdots 5 \Rightarrow 10 + 15 + 12 = 37\not \vdots 5\)
2. Tính chất chia hết của 1 hiệu
Nếu số trừ và số bị trừ đều chia hết cho cùng 1 số thì hiệu chia hết cho số đó
3. Tính chất chia hết của 1 tích
Nếu 1 thừa số của tích chia hết cho 1 số thì tích chia hết cho số đó
Phương pháp:
Áp dụng tính chất 1 và tính chất 2 về sự chia hết của một tổng, một hiệu.
Ví dụ:
a)
Ta có \(6 \vdots 3;\,9 \vdots 3;\,15 \vdots 3\, \Rightarrow 6 + 9 + 15 = 30 \vdots 3\)
b)
Ta có: \(75 \vdots 15\) và \(12\not \vdots 15\) nên \(75 + 12\not \vdots 15\) và \(75 - 12\not \vdots 15\)
c)
\(10 \vdots 5;\,15 \vdots 5;\,12\not \vdots 5 \Rightarrow 10 + 15 + 12 = 37\not \vdots 5\).
Phương pháp:
Áp dụng tính chất 1 và tính chất 2 để tìm điều kiện của số hạng chưa biết.
Ví dụ:
Cho tổng \(M = 105 + 72 + x\) . Để $M$ chia hết cho $3$ thì $x$ phải như thế nào?
Giải:
Vì \(105\, \vdots \,3;\,72\, \vdots \,3\) nên để \(M = 105 +72 + x\) chia hết cho \(3\) thì \(x\, \vdots \,3\).
Phương pháp:
Áp dụng tính chất: Nếu trong một tích các số tự nhiên có một thừa số chia hết cho một số nào đó thì tích cũng chia hết cho số đó.
Ví dụ:
Nếu $n$ chia hết cho $13$ thì $2n$ cũng chia hết cho $13$.
Trong chương trình Toán 6, kiến thức về quan hệ chia hết là một trong những nền tảng quan trọng để học sinh tiếp cận các khái niệm toán học phức tạp hơn. Bài viết này sẽ trình bày chi tiết về lý thuyết quan hệ chia hết, tính chất chia hết, cùng với các ví dụ minh họa và bài tập thực hành để giúp học sinh hiểu rõ và vận dụng kiến thức một cách hiệu quả.
Định nghĩa: Nếu có hai số nguyên a và b (b ≠ 0) sao cho tồn tại một số nguyên q thỏa mãn a = bq, ta nói a chia hết cho b, ký hiệu là a ⋮ b. Số a gọi là số bị chia, số b gọi là số chia, số q gọi là thương.
Ví dụ:
Tính chất 1: Nếu a ⋮ b và c ⋮ b thì (a + c) ⋮ b.
Ví dụ: 6 ⋮ 2 và 8 ⋮ 2 thì (6 + 8) ⋮ 2, tức là 14 ⋮ 2.
Tính chất 2: Nếu a ⋮ b và c ⋮ b thì (a - c) ⋮ b.
Ví dụ: 10 ⋮ 5 và 5 ⋮ 5 thì (10 - 5) ⋮ 5, tức là 5 ⋮ 5.
Tính chất 3: Nếu a ⋮ b và m là một số tự nhiên thì a.m ⋮ b.
Ví dụ: 4 ⋮ 2 thì 4.3 ⋮ 2, tức là 12 ⋮ 2.
Tính chất 4: Nếu a ⋮ b và b ⋮ c thì a ⋮ c.
Ví dụ: 12 ⋮ 3 và 3 ⋮ 1 thì 12 ⋮ 1.
Mọi số nguyên đều chia hết cho 1 và -1.
Số 0 chia hết cho mọi số khác 0.
Một số khác 0 chỉ chia hết cho chính nó và 1 (hoặc -1).
Kiến thức về quan hệ chia hết là cơ sở để học sinh hiểu và vận dụng các khái niệm như ước số, bội số, số nguyên tố, phân số,… trong các bài học tiếp theo. Việc nắm vững lý thuyết và thực hành các bài tập liên quan sẽ giúp học sinh xây dựng nền tảng toán học vững chắc.
| Tính chất | Mô tả |
|---|---|
| 1 | Nếu a ⋮ b và c ⋮ b thì (a + c) ⋮ b |
| 2 | Nếu a ⋮ b và c ⋮ b thì (a - c) ⋮ b |
| 3 | Nếu a ⋮ b và m là số tự nhiên thì a.m ⋮ b |
| 4 | Nếu a ⋮ b và b ⋮ c thì a ⋮ c |
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết quan hệ chia hết và tính chất chia hết trong chương trình Toán 6 Cánh diều. Chúc bạn học tập tốt!