Chào mừng các em học sinh đến với bài học lý thuyết về phép nhân và phép chia các số tự nhiên trong chương trình Toán 6 Cánh diều. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về hai phép tính này.
Chúng ta sẽ cùng nhau tìm hiểu về ý nghĩa của phép nhân, phép chia, các tính chất của chúng và cách áp dụng vào giải các bài toán thực tế.
Lý thuyết Phép nhân, phép chia các số tự nhiên Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
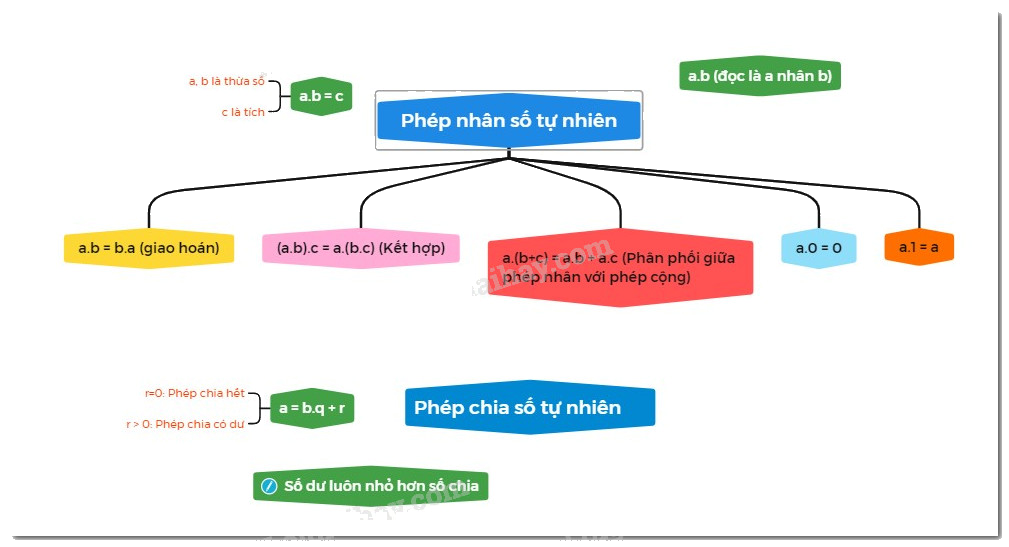
1. Phép nhân
\(a.b = a + a + ... + a\) (Có b số hạng)
\(a.b = d\)
(thừa số) . (thừa số) = (tích)
Tính chất của phép nhân:
Giao hoán: \[a.b = b.a\]
Kết hợp: \[\left( {a.b} \right).c = a.\left( {b.c} \right)\]
Phân phối của phép nhân đối với phép cộng:\(a.\left( {b + c} \right) = a.b + a.c\)
Ta hiểu tính chất phân phối ở đây là nếu a nhân với một tổng của b và c thì ta lấy a nhân với b và lấy a nhân với c rồi cộng lại với nhau. Chẳng hạn, \[2.\left( {3 + 5} \right) = 2.3 + 2.5\].
Lưu ý:
1) Nếu các thừa số đều bằng chữ, hoặc chỉ có một thừa số bằng số thì ta có thể không viết dấu nhân giữa các thừa số. Chẳng hạn, \(a \times b = a.b = ab\), \(2 \times a = 2.a = 2a\).
2) Trong tính nhẩm ta thường sử dụng các kết quả:
2.5=10
4.25=100
8.125=1000
3) Tích \(\left( {ab} \right)c\) hay \(a\left( {bc} \right)\) gọi là tích cả ba số a, b, c và viết gọn là \(abc\).
Ví dụ 1: Đặt tính nhân \(254.45\)
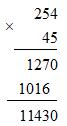
Ví dụ 2: Tính nhẩm 12.25
\(12.25 = \left( {3.4} \right).25 = 3.\left( {4.25} \right) = 3.100 = 300\)
2. Phép chia hết và phép chia có dư
Chia hai số tự nhiên
Cho hai số tự nhiên \(a\) và \(b,\) trong đó \(b \ne 0\), ta luôn tìm được đúng hai số tự nhiên \(q\) và \(r\) duy nhất sao cho:
\(a = b.q + r\) trong đó \(0 \le r < b\)
Nếu \(r = 0\) thì ta có phép chia hết:
(số bị chia) : (số chia) = (thương)
Nếu \(r \ne 0\) thì ta có phép chia có dư.
(số bị chia) = (số chia) . (thương) + (số dư)
Ví dụ 3: Thực hiện các phép chia sau
a) 780:12
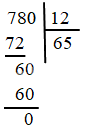
b) 445:13
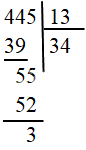
CÁC DẠNG TOÁN VỀ PHÉP NHÂN SÓ TỰ NHIÊN
Phương pháp:
- Quan sát, phát hiện các đặc điểm của các thừa số.
- Từ đó, xét xem nên áp dụng tính chất nào (giao hoán, kết hợp, phân phối) để tính một cách nhanh chóng.
Đặc biệt: Viết một số dưới dạng một tích để tính nhanh
Phương pháp:
Bước 1: Căn cứ theo yêu cầu của đề bài, ta có thể viết một số tự nhiên đã cho dưới dạng một tích của hai hay nhiều thừa số.
Bước 2: Sử dụng tính chất giao hoán, kết hợp và phân phối để tính một cách hợp lí.
Phương pháp:
+ Để tìm số chưa biết trong một phép tính, ta cần nắm vững quan hệ giữa các số trong phép tính. Chẳng hạn: thừa số bằng tích chia cho thừa số đã biết,…
+ Đặc biệt cần chú ý: với mọi $a$\( \in \)$N$ ta đều có $a.0 = 0;a.1 = a.$
+ Nếu tích hai thừa số bằng 0 thì có ít nhất một thừa số bằng 0.
Ví dụ:
Tìm $x$, biết $x.5=65$.
Giải:
$x.5=65$
$x=65:5$
$x=13$
Phương pháp:
Nhận xét, phát hiện và sử dụng các đặc điểm của các thừa số trong tổng hoặc tích. Từ đó dựa vào các tính chất phép nhân để rút ra kết luận.
Ví dụ:
So sánh hai tích sau mà không tính giá trị của chúng
\(A = 2018.2018;B = 2017.2019\)
Giải:
Ta có:
\(\begin{array}{l}A = 2018.2018\\ = 2018.\left( {2017 + 1} \right)\\ = 2018.2017 + 2018.1\\ = 2018.2017 + 2018\\=2017.2018+2018\\B = 2017.2019\\ = 2017.\left( {2018 + 1} \right)\\ = 2017.2018 + 2017.1\\ = 2017.2018 + 2017\\ A= 2017.2018 + 2018=2017.2018+2017+1\\ = B + 1\\ \Rightarrow A = B+ 1\end{array}\)
Vì \(B+1 > B\) nên \(A > B\).
Phương pháp:
Dựa vào điều kiện xác định các chữ số trong số tự nhiên cần tìm để tìm từng chữ số có mặt trong số tự nhiên đó.
Ví dụ:
Tìm một số tự nhiên có hai chữ số, biết rằng khi thêm 21 vào bên trái số đó thì được một số mới gấp 31 lần số cần tìm.Giải:
Gọi số cần tìm là \(\overline {ab} \), khi viết thêm số 21 vào bên trái số đó ta được số \(\overline {21ab} \).
Vì \(\overline {21ab} \) gấp 31 lần \(\overline {ab} \) nên ta có:
\(\begin{array}{l}\overline {ab} \times 31 = \overline {21ab} \\\overline {ab} \times 31 = 2100 + \overline {ab} \\\overline {ab} \times 31 - \overline {ab} \times 1 = 2100\\\overline {ab} \times \left( {31 - 1} \right) = 2100\\\overline {ab} \times 30 = 2100\\\overline {ab} = 2100:30\\\overline {ab} = 70\end{array}\)
Phép nhân và phép chia các số tự nhiên là hai phép tính cơ bản trong toán học, đóng vai trò quan trọng trong việc giải quyết các bài toán hàng ngày và là nền tảng cho các kiến thức toán học nâng cao hơn. Trong chương trình Toán 6 Cánh diều, việc nắm vững lý thuyết về hai phép tính này là vô cùng cần thiết.
a. Ý nghĩa của phép nhân: Phép nhân là một phép toán biểu thị sự cộng nhiều lần một số. Ví dụ: 3 x 4 có nghĩa là cộng số 3 với chính nó 4 lần (3 + 3 + 3 + 3 = 12).
b. Các tính chất của phép nhân:
c. Ví dụ minh họa:
Tính: 5 x 7 = ?
Áp dụng ý nghĩa của phép nhân, ta có: 5 x 7 = 5 + 5 + 5 + 5 + 5 + 5 + 5 = 35
a. Ý nghĩa của phép chia: Phép chia là một phép toán biểu thị sự chia một số thành các phần bằng nhau. Ví dụ: 12 : 3 = 4 có nghĩa là chia số 12 thành 3 phần bằng nhau, mỗi phần có 4 đơn vị.
b. Mối quan hệ giữa phép nhân và phép chia: Phép nhân và phép chia là hai phép toán ngược nhau. Nếu a x b = c thì c : a = b và c : b = a.
c. Số chia hết và số dư:
d. Ví dụ minh họa:
Tính: 20 : 4 = ?
Áp dụng mối quan hệ giữa phép nhân và phép chia, ta có: 4 x 5 = 20, do đó 20 : 4 = 5
Bài 1: Tính:
Bài 2: Điền vào chỗ trống:
a) 7 x … = 42
b) … : 5 = 8
Khi thực hiện phép nhân và phép chia các số tự nhiên, cần chú ý đến thứ tự thực hiện các phép toán. Nếu trong một biểu thức có cả phép nhân và phép chia, ta thực hiện các phép tính theo thứ tự từ trái sang phải.
Việc hiểu rõ lý thuyết và thực hành thường xuyên các bài tập sẽ giúp các em nắm vững kiến thức về phép nhân và phép chia các số tự nhiên, từ đó đạt kết quả tốt trong môn Toán.
Bài học hôm nay đã cung cấp cho các em những kiến thức cơ bản và quan trọng về lý thuyết phép nhân, phép chia các số tự nhiên trong chương trình Toán 6 Cánh diều. Hy vọng rằng, với những kiến thức này, các em sẽ tự tin hơn trong việc giải quyết các bài toán liên quan đến hai phép tính này.