Chào mừng các em học sinh lớp 6 đến với bài học về Lý thuyết Phép tính lũy thừa với số mũ tự nhiên trong chương trình Toán 6 Cánh diều. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về lũy thừa, giúp các em giải quyết các bài toán liên quan một cách dễ dàng.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, các tính chất và cách áp dụng của phép tính lũy thừa. Giaitoan.edu.vn cam kết mang đến cho các em một trải nghiệm học tập hiệu quả và thú vị.
Lý thuyết Phép tính lũy thừa với số mũ tự nhiên Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
I. Lũy thừa
Lũy thừa với số mũ tự nhiên
Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a:
\({a^n} = a.a \ldots ..a\) (\(n\) thừa số \(a\) ) (\(n \notin \mathbb{N}^*\) )
\({a^n}\) đọc là “a mũ n” hoặc “a lũy thừa n”.
\(a\) được gọi là cơ số.
\(n\) được gọi là số mũ.
Phép nhân nhiều thừa số giống nhau như trên được gọi là phép nâng lên lũy thừa.
\({a^1} = a\)
\({a^2} = a.a\) gọi là “\(a\) bình phương” (hay bình phương của \(a\)).
\({a^3} = a.a.a\) gọi là “\(a\) lập phương” (hay lập phương của \(a\)).
Với \(n\) là số tự nhiên khác 0 (thuộc \(\mathbb{N}^*\)), ta có: \({10^n} = 1\underbrace {0...0}_{n{\rm{ \,chữ\, số\, 0}}}\)(số mũ là n thì có n chữ số 0 đằng sau chữ số 1)
Quy ước: \({a^1} = a\); \({a^0} = 1\left( {a \ne 0} \right).\)
Ví dụ:
a) \({8^3}\) đọc là “tám mũ ba”, có cơ số là 8 và số mũ là 3.
b) Tính \({2^3}\).
Số trên là lũy thừa bậc 3 của 2 và là tích của 3 thừa số 2 nhân với nhau nên ta có:
\({2^3} = 2.2.2 = 8\)
c) Tính \({10^3}\)
\({10^3}\) có số mũ là 3 nên \({10^3} = 1000\)(Sau chữ số 1 có 3 chữ số 0).
d) Viết 10 000 000 dưới dạng lũy thừa của 10:
Cách 1: \(10000000 = 10.10.10.10.10.10.10\)\( = {10^7}\)
Cách 2: Sau chữ số 1 có 7 chữ số 0 nên \(10000000 = {10^7}\)
e) Viết 16 dưới dạng lũy thừa cơ số 4:
\(16 = 4.4 = {4^2}\)
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.
\({a^m}.{a^n} = {a^{m + n}}\)
Ví dụ:
a) \({3.3^5} = {3^1}{.3^5} = {3^{1 + 5}} = {3^6}.\)
b) \({5^2}{.5^4} = {5^{2 + 4}} = {5^6}\)
c) \({a^3}.{a^5} = {a^{3 + 5}} = {a^8}\)
d) \(x.{x^8} = {x^1}.{x^8} = {x^{1 + 8}} = {x^9}\)
e) \({4^2}.64 = {4^2}.4.4.4 = {4^2}{.4^3} = {4^{2 + 3}} = {4^5}\)
f) \(10.2.5 = 10.\left( {2.5} \right) = 10.10 = {10^2}\) (Sử dụng tính chất kết hợp trong phép nhân trước).
Phép chia hai lũy thừa cùng cơ số
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ cho nhau.
\({a^m}:{a^n} = {a^{m - n}}\)\(\left( {a \ne 0;\,m \ge n \ge 0} \right)\)
Ví dụ:
a) \({3^5}:3 = {3^5}:{3^1} = {3^{5 - 1}} = {3^4}\)\( = 3.3.3.3 = 81\)
b) \({a^6}:{a^2} = {a^{6 - 2}} = {a^4}\)
c) \({2^3}:{2^3} = {2^{3 - 3}} = {2^0} = 1\)
d) \(81:{3^2} = {3^4}:{3^2} = {3^{4 - 2}} = {3^2} = 3.3 = 9\)
Lưu ý:
Phép chia hai lũy thừa cùng cơ số không thể lấy hai số mũ chia cho nhau mà phải lấy hai số mũ trừ cho nhau.
Phương pháp giải
Áp dụng công thức: $\underbrace {a.a.a.....a}_{n\,{\rm{thua}}\,{\rm{so}}}$$ = {a^n};$${a^m}.{a^n} = {a^{m + n}};{a^m}:{a^n} = {a^{m - n}}\left( {a \ne 0,m \ge n} \right)$
Phương pháp giải
Bước 1: Xác định cơ số và số mũ.
Bước 2: Áp dụng công thức:${a^m}.{a^n} = {a^{m + n}};{a^m}:{a^n} = {a^{m - n}}\left( {a \ne 0,m \ge n} \right)$
Phương pháp giải
Để so sánh các số viết dưới dạng lũy thừa, ta có thể làm theo:
Cách 1: Đưa về cùng cơ số là số tự nhiên, rồi so sánh hai số mũ
Nếu \(m > n\) thì \({a^m} > {a^n}\)
Cách 2: Đưa về cùng số mũ rồi so sánh hai cơ số
Nếu \(a > b\) thì \({a^m} > {b^m}\)
Cách 3: Tính cụ thể rồi so sánh
Ngoài ra ta còn sử dụng tính chất bắc cầu: Nếu \(a < b;b < c\) thì \(a < c.\)
Phương pháp giải
Bước 1: Đưa về hai luỹ thừa của cùng một cơ số.
Bước 2: Sử dụng tính chất
Với \(a \ne 0;a \ne 1\), nếu ${a^m} = {a^n}$ thì $m = n\,\,(a,m,n \in N)$
Phương pháp giải
Cách 1: Dùng định nghĩa lũy thừa
$\underbrace {a.a.....a}_{n\,{\rm{thừa}}\,{\rm{số}}\,a}$ $ = {a^n}$ Cách 2: Sử dụng tính chất
Với \(a;b \ne 0;a;b \ne 1\), nếu ${a^m} = {b^m}$ thì $a = n\,\,(a,b,m,n \in N)$.
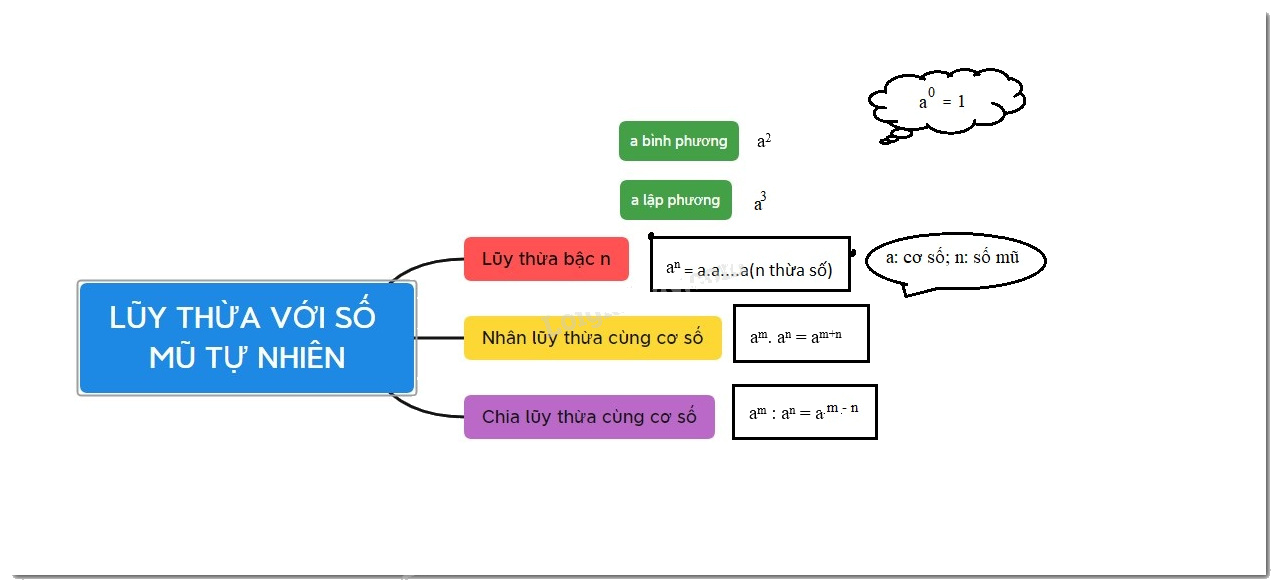
Phép tính lũy thừa là một trong những khái niệm cơ bản và quan trọng trong toán học, đặc biệt là ở chương trình Toán 6. Hiểu rõ lý thuyết về phép tính lũy thừa với số mũ tự nhiên là nền tảng để các em học sinh tiếp cận các kiến thức toán học phức tạp hơn ở các lớp trên.
Lũy thừa của một số a (gọi là cơ số) với số mũ tự nhiên n (n ≥ 1) là tích của n thừa số a, ký hiệu là an. Ví dụ: 23 = 2 × 2 × 2 = 8.
Có một số trường hợp đặc biệt cần lưu ý khi làm việc với lũy thừa:
Phép tính lũy thừa có một số tính chất quan trọng sau:
Hãy cùng xem xét một số ví dụ để hiểu rõ hơn về cách áp dụng các tính chất của phép tính lũy thừa:
Để củng cố kiến thức về phép tính lũy thừa, các em hãy thử giải các bài tập sau:
Khi thực hiện các phép tính với lũy thừa, các em cần lưu ý:
Hy vọng rằng bài học về Lý thuyết Phép tính lũy thừa với số mũ tự nhiên Toán 6 Cánh diều này đã cung cấp cho các em những kiến thức cần thiết và hữu ích. Hãy tiếp tục luyện tập và khám phá thêm nhiều điều thú vị trong thế giới toán học!