Góc là một khái niệm cơ bản và quan trọng trong hình học, đặc biệt là chương trình Toán 6 Cánh Diều. Việc nắm vững lý thuyết góc không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng cho các kiến thức toán học nâng cao hơn.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu về lý thuyết góc Toán 6 Cánh Diều, giúp học sinh tiếp thu kiến thức một cách hiệu quả nhất.
Lý thuyết Góc Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
I. Góc
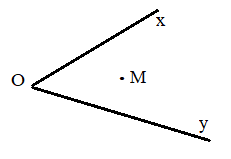
Góc là hình gồm hai tia chung gốc. Gốc chung của hai tia gọi là đỉnh của góc. Hai tia là hai cạnh của góc.
Chú ý:
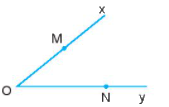
Trong hình trên:
- Góc \(xOy\) (hoặc \(yOx\)) được kí hiệu là \(\widehat {xOy}\) (hoặc \(\angle xOy\)).
- Hai tia \(Ox\) và \(Oy\) được gọi là hai cạnh của góc. Gốc chung của hai tia được gọi là đỉnh của góc.
- Góc \(xOy\) còn có cách gọi khác là: góc \(AOB\), góc \(O\), góc \(yOx\), góc \(BOA\).
Để vẽ \(\widehat {xOy}\), ta vẽ điểm \(O\) trên giấy hoặc bảng, từ điểm \(O\) vẽ hai tia \(Ox\) và \(Oy\).
Ta được \(\widehat {xOy}\).
Khi \(Ox\) và \(Oy\) là hai tia đối nhau, ta có góc bẹt \(xOy\).
Cho góc xOy khác góc bẹt. Điểm M được gọi là điểm trong của góc xOy không bẹt nếu tia OM cắt một đoạn thẳng nối hai điểm trên hai cạnh tại một điểm nằm giữa hai điểm đó.
Ví dụ: Trong hình dưới đây, M là điểm trong của \(\widehat {xOy}\).
a) Thước đo góc
Thước đo góc có dạng nửa hình tròn và được chia đều thành 180 phần bằng nhau, mỗi phần ứng với \({1^o}\).
b) Cách đo góc
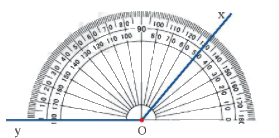
- Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh O của góc.
- Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh Oy) đi qua vạch 0 của thước và thước chồng lên phần trong của góc như trên.
- Bước 3: Xác định xem cạnh còn lại của góc (cạnh Ox) đi qua vạch chỉ số nào trên thước đo góc, ta sẽ được số đo của góc đó.
Ví dụ:
Trong hình bên trên, tia Ox đi qua vạch chỉ số 130, vậy góc xOy có số đo là 130°.
Ta viết \(\widehat {xOy} = {130^o}.\)
c) Số đo góc
Mỗi góc có một số đo. Số đo của góc bẹt là \({180^o}\).
Số đo của mỗi góc không vượt quá \({180^o}\).
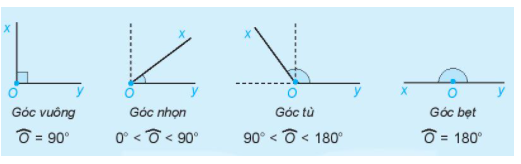
- Góc có số đo bằng \({90^o}\) là góc vuông
- Góc bẹt có số đo bằng \({180^o}\)
- Góc có số đo nhỏ hơn \({90^o}\) là góc nhọn
- Góc có số đo lơn hơn \({90^o}\) nhưng nhỏ hơn \({180^o}\) là góc tù.
Trong chương trình Toán 6 Cánh Diều, học sinh bắt đầu làm quen với khái niệm góc, các loại góc và cách đo góc. Đây là một trong những kiến thức nền tảng quan trọng để xây dựng các kiến thức hình học phức tạp hơn ở các lớp trên. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết góc Toán 6 Cánh Diều, giúp học sinh hiểu rõ và áp dụng kiến thức vào giải bài tập.
Góc là hình được tạo bởi hai tia chung gốc. Tia chung gốc gọi là cạnh của góc, gốc chung gọi là đỉnh của góc.
Ví dụ: Góc xOy được tạo bởi hai tia Ox và Oy, gốc O là đỉnh của góc.
Dựa vào số đo của góc, ta có các loại góc sau:
Góc được đo bằng độ (°). Để đo góc, ta sử dụng thước đo góc. Cách sử dụng thước đo góc:
Góc kề nhau: Hai góc có chung cạnh và không có điểm chung bên trong. Ví dụ: Góc xOy và góc yOz là hai góc kề nhau nếu Oy là cạnh chung.
Góc phụ nhau: Hai góc kề nhau có tổng số đo bằng 90°. Ví dụ: Nếu góc xOy = 30° và góc yOz = 60°, thì góc xOy và góc yOz là hai góc phụ nhau.
Góc bù nhau: Hai góc kề nhau có tổng số đo bằng 180°. Ví dụ: Nếu góc xOy = 120° và góc yOz = 60°, thì góc xOy và góc yOz là hai góc bù nhau.
Bài 1: Cho góc xOy có số đo bằng 60°. Tính số đo của góc kề bù với góc xOy.
Giải: Góc kề bù với góc xOy là góc yOz. Vì góc xOy và góc yOz kề bù nên xOy + yOz = 180°. Suy ra yOz = 180° - 60° = 120°.
Bài 2: Cho hai góc kề nhau xOy và yOz có tổng số đo bằng 90°. Hỏi hai góc này có phải là hai góc phụ nhau không? Vì sao?
Giải: Vì hai góc xOy và yOz kề nhau và có tổng số đo bằng 90° nên hai góc này là hai góc phụ nhau.
Lý thuyết góc có ứng dụng rộng rãi trong thực tế, ví dụ như:
Lý thuyết góc Toán 6 Cánh Diều là một phần quan trọng của chương trình học. Việc nắm vững lý thuyết này sẽ giúp học sinh có một nền tảng vững chắc để học tập các môn học khác và ứng dụng vào thực tế. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết góc Toán 6 Cánh Diều.