Chào mừng các em học sinh đến với bài học về lý thuyết Hình chữ nhật và Hình thoi trong chương trình Toán 6 Cánh diều. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về hai hình học này.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất, dấu hiệu nhận biết và các ứng dụng thực tế của Hình chữ nhật và Hình thoi.
Lý thuyết Hình chữ nhật. Hình thoi Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
1. Hình chữ nhật
Một số yếu tố cơ bản của hình chữ nhật
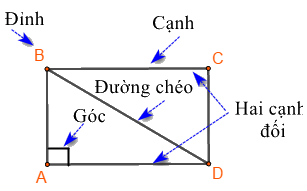
- Bốn góc bằng nhau và bằng \({90^0}\)
- Các cạnh đối bằng nhau.
- Hai đường chéo bằng nhau.
Ví dụ:
Hình chữ nhật \(ABCD\) có:
- Bốn đỉnh A, B, C, D
- Hai cặp cạnh đối diện bằng nhau: \(AB = CD;\,\,BC = AD\).
- Hai cặp cạnh đối diện song song: AB song song với CD; BC song song với AD.
- Bốn góc ở đỉnh A, B, C, D bằng nhau và bằng góc vuông.
- Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường:
\(AC = BD\) và \(OA = OC;\,\,OB = OD\).
Cách vẽ hình chữ nhật có hai cạnh là a và b:
Bước 1: Vẽ đoạn thẳng \(AB = a\left( {cm} \right)\)
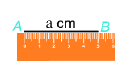
Bước 2: Vẽ đường thẳng vuông góc với \(AB\) tại \(A\). Trên đường thẳng đó, lấy điểm \(D\) sao cho \(AD = b\left( {cm} \right)\)
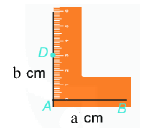
Bước 3: Vẽ đường thẳng vuông góc với \(AB\) tại \(B\). Trên đường thẳng đó, lấy điểm \(C\) sao cho \(BC = b\left( {cm} \right)\)
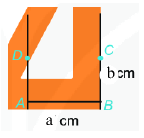
Bước 4: Nối \(C\) và \(D\) ta được hình chữ nhật ABCD.
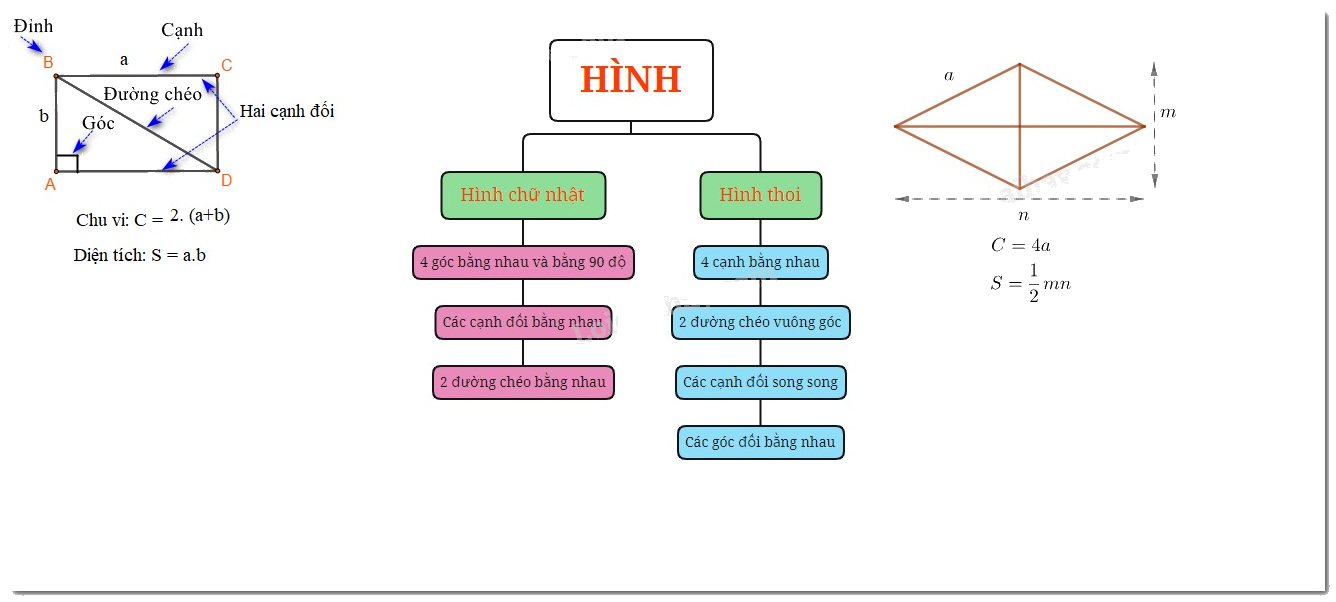
Chu vi và diện tích hình chữ nhật
Hình chữ nhật có độ dài 2 cạnh là a,b thì
Chu vi là: C=2(a+b)
Diện tích là: S=a.b
2. Hình thoi
Một số yếu tố cơ bản của hình thoi
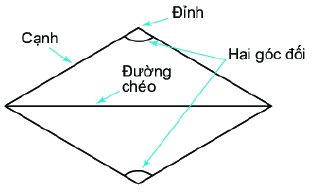
- Bốn cạnh bằng nhau
- Hai đường chéo vuông góc với nhau.
- Các cạnh đối song song với nhau
- Các góc đối bằng nhau
Cách vẽ hình thoi có cạnh là a:
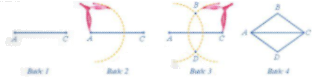
Bước 1: Dùng thước vẽ đoạn thẳng AC
Bước 2: Dùng compa vẽ một phần đường tròn tâm A bán kính AB
Bước 3: Dùng compa vẽ một phần đường tròn tâm C bán kính AB; phần đường tròn này cắt phần đường tròn owrt bước 2 tại 2 điểm B, D
Bước 4: Dùng thước vẽ các đoạn thẳng AB,BC,CD,DA
Chu vi và diện tích của hình thoi
Hình thoi có độ dài cạnh là a, 2 đường chéo là m,n thì
Chu vi là: C=4.a
Diện tích là: S=\(\frac{1}{2}. m.n\)
Trong chương trình Toán 6, Hình chữ nhật và Hình thoi là hai hình học quan trọng, là nền tảng cho các kiến thức hình học nâng cao hơn. Việc nắm vững lý thuyết và các tính chất của hai hình này là vô cùng cần thiết để giải quyết các bài tập và ứng dụng vào thực tế.
1. Định nghĩa: Hình chữ nhật là hình có bốn góc vuông.
2. Tính chất:
3. Dấu hiệu nhận biết:
4. Diện tích hình chữ nhật: Diện tích hình chữ nhật bằng tích độ dài hai cạnh kề nhau. S = a * b (a, b là chiều dài và chiều rộng).
5. Chu vi hình chữ nhật: Chu vi hình chữ nhật bằng tổng độ dài tất cả các cạnh. P = 2 * (a + b).
1. Định nghĩa: Hình thoi là hình có bốn cạnh bằng nhau.
2. Tính chất:
3. Dấu hiệu nhận biết:
4. Diện tích hình thoi: Diện tích hình thoi bằng nửa tích độ dài hai đường chéo. S = (d1 * d2) / 2 (d1, d2 là độ dài hai đường chéo).
5. Chu vi hình thoi: Chu vi hình thoi bằng bốn lần độ dài một cạnh. P = 4 * a (a là độ dài cạnh).
Hình chữ nhật là một trường hợp đặc biệt của hình bình hành, và hình thoi cũng là một trường hợp đặc biệt của hình bình hành. Hình vuông là hình vừa là hình chữ nhật, vừa là hình thoi.
Bài 1: Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Tính diện tích và chu vi của hình chữ nhật.
Bài 2: Cho hình thoi MNPQ có đường chéo MP = 10cm, NQ = 8cm. Tính diện tích của hình thoi.
Bài 3: Chứng minh rằng trong hình chữ nhật, hai đường chéo bằng nhau.
Hi vọng bài học về lý thuyết Hình chữ nhật và Hình thoi Toán 6 Cánh diều này đã giúp các em hiểu rõ hơn về hai hình học quan trọng này. Hãy luyện tập thêm nhiều bài tập để củng cố kiến thức và áp dụng vào giải quyết các bài toán thực tế. Chúc các em học tốt!