Lý thuyết Ôn tập chương 2. Số nguyên

Lý thuyết Ôn tập Chương 2: Số nguyên

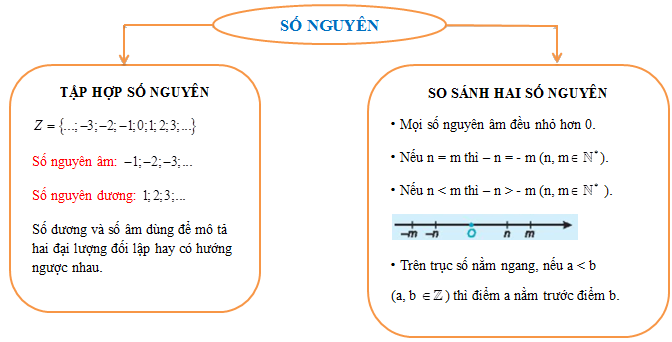
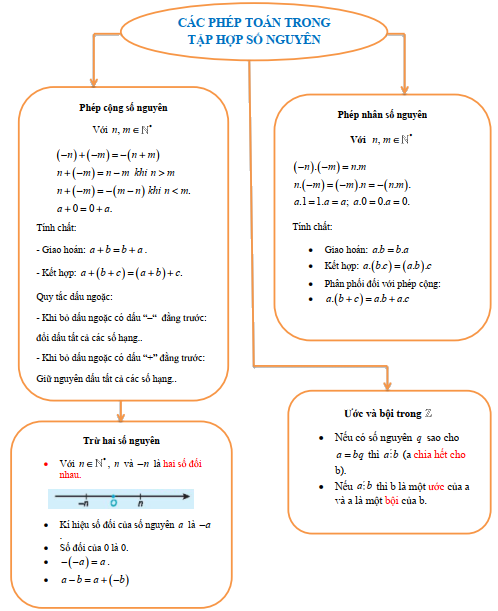
Chương 2 trong chương trình Toán lớp 6 và lớp 7 tập trung vào việc giới thiệu và nghiên cứu về số nguyên. Đây là một bước tiến quan trọng trong việc mở rộng khái niệm về số, từ các số tự nhiên quen thuộc đến các số âm và số 0. Việc nắm vững lý thuyết về số nguyên là nền tảng để giải quyết các bài toán phức tạp hơn trong các chương trình học tiếp theo.

1. Số nguyên là gì?

Số nguyên bao gồm các số tự nhiên (0, 1, 2, 3,...), các số âm (-1, -2, -3,...), và số 0. Tập hợp các số nguyên được ký hiệu là ℤ.

• Số tự nhiên: Là các số dùng để đếm, bắt đầu từ 0.
• Số nguyên âm: Là các số nhỏ hơn 0, được viết dưới dạng dấu trừ (-) trước một số tự nhiên.
• Số 0: Không phải là số tự nhiên, cũng không phải là số nguyên âm.

2. Biểu diễn số nguyên trên trục số

Trục số là một đường thẳng, trên đó ta chọn một điểm làm gốc (thường là số 0). Các số nguyên dương được biểu diễn ở phía bên phải gốc, các số nguyên âm được biểu diễn ở phía bên trái gốc. Khoảng cách từ một số nguyên đến gốc trên trục số được gọi là giá trị tuyệt đối của số đó.

Giá trị tuyệt đối của một số nguyên a, ký hiệu là |a|, được định nghĩa như sau:

• Nếu a ≥ 0 thì |a| = a
• Nếu a < 0 thì |a| = -a

3. So sánh số nguyên

Để so sánh hai số nguyên, ta thực hiện theo các quy tắc sau:

1. Trong hai số nguyên âm, số nào có giá trị tuyệt đối lớn hơn thì nhỏ hơn. Ví dụ: -5 < -2 (vì |-5| = 5 > |-2| = 2)
2. Số nguyên âm luôn nhỏ hơn số nguyên dương. Ví dụ: -3 < 1
3. Số 0 lớn hơn mọi số nguyên âm. Ví dụ: 0 > -4

4. Các phép toán trên số nguyên

a. Phép cộng số nguyên

Để cộng hai số nguyên, ta thực hiện theo các quy tắc sau:

• Cộng hai số nguyên dương: Cộng như cộng hai số tự nhiên.
• Cộng một số nguyên dương và một số nguyên âm: Thực hiện như trừ hai số tự nhiên, lấy dấu của số có giá trị tuyệt đối lớn hơn.
• Cộng hai số nguyên âm: Cộng hai giá trị tuyệt đối của chúng, rồi đặt dấu trừ (-) trước kết quả.

b. Phép trừ số nguyên

Phép trừ số nguyên được thực hiện bằng cách đổi dấu số trừ và thực hiện phép cộng. Ví dụ: a - b = a + (-b)

c. Phép nhân số nguyên

Để nhân hai số nguyên, ta thực hiện theo các quy tắc sau:

• Nhân hai số nguyên cùng dấu: Nhân hai giá trị tuyệt đối của chúng, rồi đặt dấu dương (+) trước kết quả.
• Nhân hai số nguyên khác dấu: Nhân hai giá trị tuyệt đối của chúng, rồi đặt dấu trừ (-) trước kết quả.

d. Phép chia số nguyên

Phép chia số nguyên cũng có các quy tắc tương tự như phép nhân về dấu. Tuy nhiên, cần lưu ý rằng không phải phép chia số nguyên nào cũng thực hiện được (ví dụ: chia cho 0).

5. Bài tập vận dụng

Để củng cố kiến thức về số nguyên, bạn có thể thực hành giải các bài tập sau:

• So sánh các số nguyên: -7, 3, -1, 0, 5
• Thực hiện các phép tính: (-2) + 5, 8 - (-3), (-4) * 2, 10 / (-2)

6. Kết luận

Việc hiểu rõ lý thuyết về số nguyên là vô cùng quan trọng trong quá trình học Toán. Hy vọng rằng tài liệu Lý thuyết Ôn tập chương 2. Số nguyên tại giaitoan.edu.vn sẽ giúp bạn nắm vững kiến thức và tự tin giải quyết các bài toán liên quan đến số nguyên.