Chào mừng các em học sinh đến với bài học về Lý thuyết Điểm và Đường thẳng trong chương trình Toán 6 Cánh diều. Đây là một trong những kiến thức cơ bản và quan trọng nhất của môn Toán, giúp các em xây dựng nền tảng vững chắc cho các bài học tiếp theo.
Bài học này sẽ cung cấp cho các em những khái niệm cơ bản về điểm, đường thẳng, cách xác định và so sánh các điểm, cũng như các tính chất quan trọng của đường thẳng.
Lý thuyết Điểm. Đường thẳng Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
1. Điểm
- Điểm là một khái niệm cơ bản của hình học, ta không định nghĩa điểm mà chỉ hình dung nó, chẳng hạn bằng một hạt bụi rất nhỏ, một chấm mực trên mặt giấy,...- Người ta thường dùng các chữ cái in hoa A, B,C, X, Y,.. để đặt tên cho điểm.
Quy ước: Khi nói 2 điểm mà không nói gì thêm, ta hiểu đó là 2 điểm phân biệt
2. Đường thẳng
Đường thẳng không bị giới hạn về 2 phía
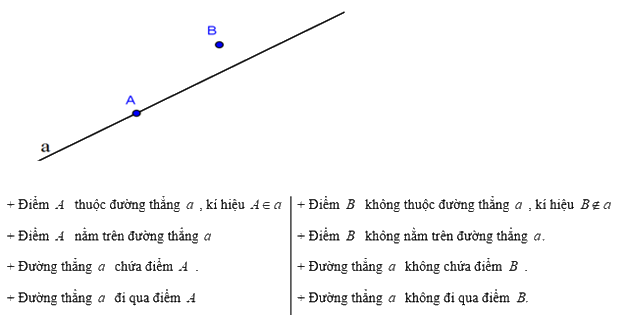
3. Điểm thuộc đường thẳng, điểm không thuộc đường thẳng
Điểm A thuộc đường thẳng d, kí hiệu \(A \in a\)
Điểm B không đường thẳng d, kí hiệu là \(B \notin a\)
Có vô số điểm thuộc đường thẳng
Để nhấn mạnh hai phía của đường thẳng, người ta còn dùng hai chữ in thường để đặt tên, ví dụ đường thẳng xy (hoặc yx)
4. Đường thẳng đi qua 2 điểm
Có 1 và chỉ 1 đường thẳng đi qua 2 điểm A và B
Đường thẳng đi qua 2 điểm A, B được gọi đường thẳng AB hay đường thẳng BA
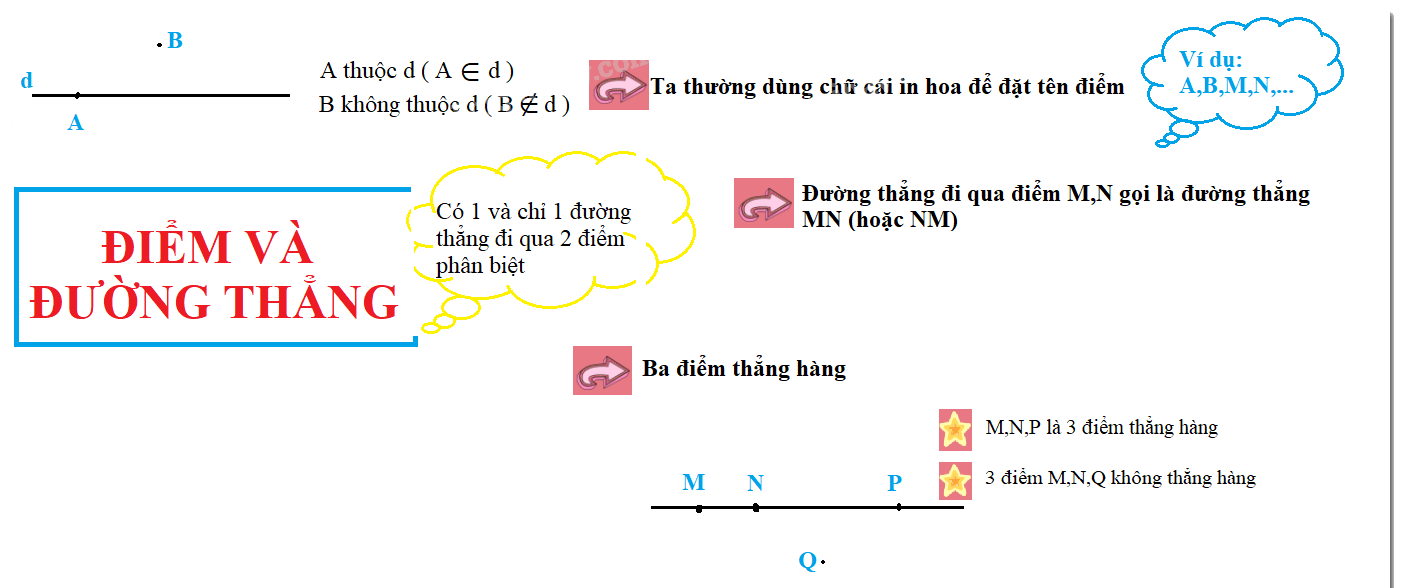
5. Ba điểm thẳng hàng
• Ba điểm phân biệt A, B, C cùng thuộc một đường thẳng được gọi là ba điểm thẳng hàng.
• Ba điểm phân biệt D, E, F không cùng thuộc bất kì một đường thẳng nào được gọi là ba điểm không thẳng hàng.
Trong ba điểm thẳng hàng, có một và chỉ một điểm nằm giữa hai điểm còn lại.
Trong chương trình Toán 6, việc nắm vững lý thuyết về điểm và đường thẳng là vô cùng quan trọng. Đây là nền tảng để hiểu và giải quyết các bài toán hình học cơ bản. Bài viết này sẽ cung cấp một cách chi tiết và dễ hiểu về lý thuyết này, dựa trên chương trình Cánh diều.
Điểm là một khái niệm cơ bản trong hình học. Chúng ta có thể hình dung điểm như một vị trí xác định trên mặt phẳng. Điểm không có kích thước, không có chiều dài, chiều rộng hay chiều cao.
Cách biểu diễn điểm: Điểm thường được ký hiệu bằng một chữ cái in hoa, ví dụ: A, B, C,...
Ví dụ: Điểm A, Điểm B, Điểm C.
Đường thẳng là một đường đi thẳng, không bị uốn cong, và kéo dài vô hạn về cả hai phía. Đường thẳng được xác định bởi hai điểm phân biệt.
Cách biểu diễn đường thẳng: Đường thẳng thường được ký hiệu bằng một chữ cái in thường, ví dụ: d, e, f,...
Ví dụ: Đường thẳng d đi qua hai điểm A và B.
Có nhiều cách để xác định một đường thẳng:
Có ba trường hợp xảy ra khi so sánh hai đường thẳng:
Bài 1: Vẽ ba điểm A, B, C sao cho ba điểm đó thẳng hàng. Vẽ đường thẳng d đi qua ba điểm đó.
Bài 2: Vẽ đoạn thẳng MN dài 5cm. Xác định trung điểm I của đoạn thẳng MN.
Bài 3: Cho hai đường thẳng a và b song song. Vẽ một đường thẳng c cắt cả hai đường thẳng a và b. Xác định các góc tạo thành.
Lý thuyết về điểm và đường thẳng là nền tảng cho nhiều kiến thức hình học khác, như góc, tam giác, đường tròn,... Việc nắm vững lý thuyết này sẽ giúp các em học tốt môn Toán và giải quyết các bài toán một cách hiệu quả.
Hy vọng bài viết này đã cung cấp cho các em những kiến thức cơ bản và quan trọng về Lý thuyết Điểm và Đường thẳng Toán 6 Cánh diều. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải các bài tập thực tế.