Chào mừng các em học sinh đến với bài học lý thuyết về phân số với tử và mẫu là số nguyên trong chương trình Toán 6 Cánh diều. Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về phân số, giúp các em hiểu rõ khái niệm, tính chất và cách thực hiện các phép toán với phân số.
Tại giaitoan.edu.vn, chúng tôi luôn cố gắng mang đến những bài giảng chất lượng, dễ hiểu và phù hợp với từng đối tượng học sinh. Hãy cùng chúng tôi khám phá thế giới của phân số ngay bây giờ!
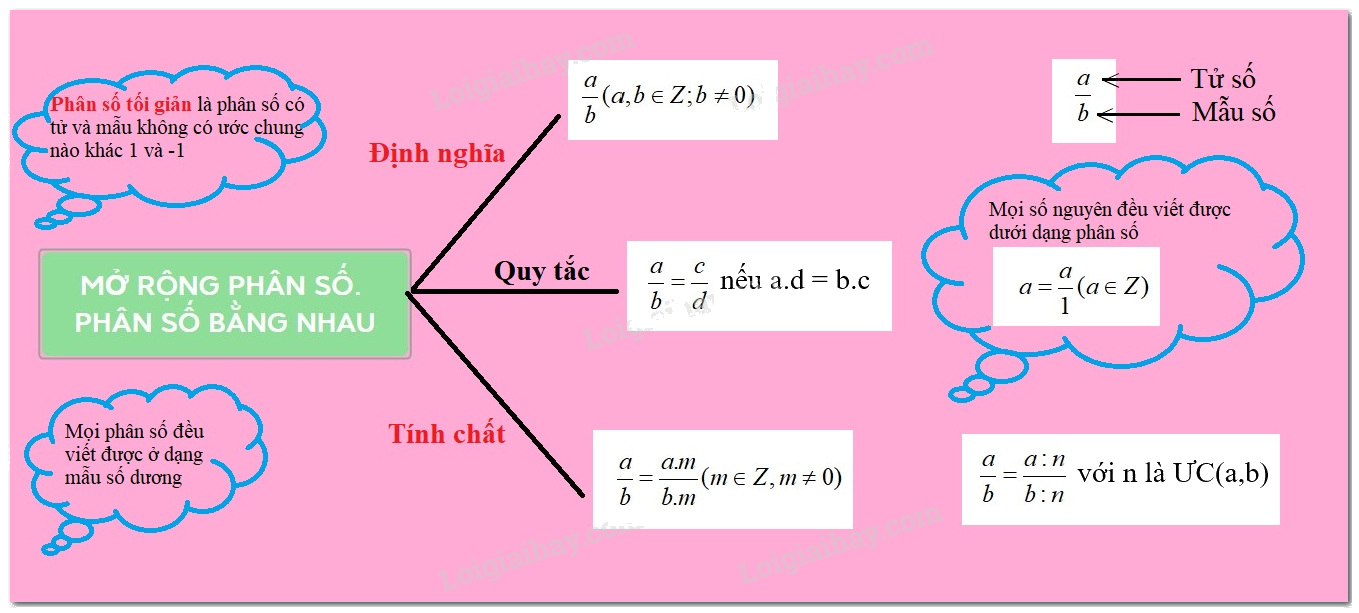
Lý thuyết Phân số với tử và mẫu là số nguyên Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
1. Khái niệm phân số
Ta gọi \(\frac{a}{b}\), trong đó \(a,\;b \in \mathbb{Z},\;b \ne 0\) là phân số, a là tử số (tử) và b là mẫu số (mẫu) của phân số. Phân số \(\frac{a}{b}\) đọc là a phần b.
2. Phân số bằng nhau
Hai phân số \(\frac{a}{b}\) và \(\frac{c}{d}\) được gọi là bằng nhau, viết là \(\frac{a}{b} = \frac{c}{d}\), nếu \(a.d = b.c\).
Chú ý: Điều kiện \(a.d = b.c\) gọi là điều kiện bằng nhau của hai phân số \(\frac{a}{b}\) và \(\frac{c}{d}\).
3. Tính chất cơ bản của phân số
* Nếu ta nhân cả tử và mẫu của một phân số với cùng 1 số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.
* Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.
Phương pháp rút gọn về phân số tối giản
Bước 1: Tìm ƯCLN của tử và mẫu sau khi đã bỏ dấu – (nếu có)
Bước 2: Chia cả tử và mẫu cho ước chung lớn nhất vừa tìm được, ta có phân số tối giản cần tìm
Để quy đồng nhiều phân số, ta thường làm như sau:
Bước 1: Viết các phân số đã cho dưới dạng phân số có mẫu dương. Tìm BCNN của các mẫu dương đó để làm mẫu số chung
Bước 2: Tìm thừa số phụ của mỗi mẫu, bằng cách chia mẫu chung cho từng mẫu
Bước 3: Nhân tử và mẫu của mỗi phân số ở Bước 1 với thừa số phụ tương ứng
Chú ý:
Mỗi số nguyên n có thể coi là phân số \(\frac{n}{1}\) (viết \(\frac{n}{1} = n\)). Khi đó số nguyên n được biểu diễn ở dạng phân số \(\frac{n}{1}.\)
Lời giải hay
Phân số là một khái niệm toán học cơ bản, xuất hiện từ rất sớm trong chương trình học. Hiểu rõ về phân số là nền tảng quan trọng để học tốt các kiến thức toán học nâng cao hơn. Bài viết này sẽ trình bày chi tiết lý thuyết về phân số với tử và mẫu là số nguyên, theo chương trình Toán 6 Cánh diều.
Một phân số là một biểu thức toán học được viết dưới dạng a/b, trong đó:
Mẫu số của phân số không được bằng 0.
Có nhiều loại phân số khác nhau, dựa trên mối quan hệ giữa tử số và mẫu số:
Tính chất cơ bản của phân số là một công cụ quan trọng để đơn giản hóa phân số và so sánh các phân số:
Việc sử dụng tính chất này giúp chúng ta rút gọn phân số về dạng đơn giản nhất.
Có nhiều cách để so sánh hai phân số:
Dưới đây là một số bài tập vận dụng để giúp các em hiểu rõ hơn về lý thuyết phân số:
Lý thuyết phân số với tử và mẫu là số nguyên là một phần quan trọng trong chương trình Toán 6. Việc nắm vững kiến thức này sẽ giúp các em học tốt các bài học tiếp theo và giải quyết các bài toán một cách hiệu quả. Hãy luyện tập thường xuyên và đừng ngần ngại hỏi thầy cô giáo nếu gặp bất kỳ khó khăn nào.
Hy vọng bài viết này đã cung cấp cho các em những kiến thức hữu ích về phân số. Chúc các em học tập tốt!