Chào mừng các em học sinh đến với bài học lý thuyết về hai bài toán phân số trong chương trình Toán 6 Cánh diều.
Bài học này sẽ cung cấp cho các em những kiến thức cơ bản và quan trọng nhất về phân số, giúp các em giải quyết các bài toán liên quan một cách hiệu quả.
Lý thuyết Hai bài toán về phân số Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
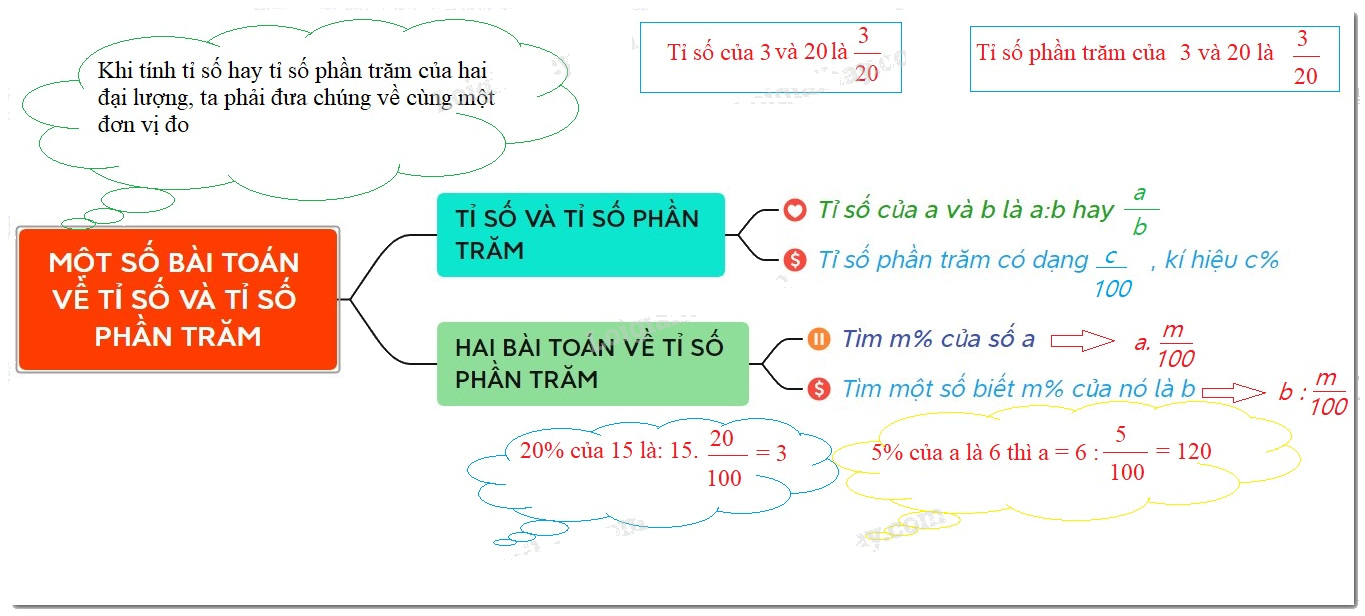
Muốn tìm $\dfrac{m}{n}$ của số $b$ cho trước, ta tính $b.\dfrac{m}{n}$ $\left( {m,n \in \mathbb{N},n \ne 0} \right)$
Ví dụ:
a) $\dfrac{2}{3}$ của $8,7$ là: $8,7.\dfrac{2}{3} = \left( {8,7:3} \right).2 = 2,9.2 = 5,8$.
b) $\dfrac{2}{3}$ của $\dfrac{{ - 15}}{2}$ là: $\dfrac{2}{3}.\dfrac{{ - 15}}{2} = - 5$.
Muốn tìm một số khi biết giá trị $\dfrac{m}{n}$ của nó bằng $a$, ta tính $a:\dfrac{m}{n}$ $\left( {m,n \in {\mathbb{N}^*}} \right)$.
Ví dụ:
Tìm một số biết $\dfrac{2}{3}$ của nó bằng $7,2$
Số cần tìm là: $7,2:\dfrac{2}{3} = 7,2.\dfrac{3}{2} = 10,8.$
Muốn tìm giá trị $a\% $ của số b, ta tính: $b.\,a\% = b.\dfrac{a}{{100}}$
Ví dụ:
$99,99\% $ của $3,75$ là: $3,75.\dfrac{{99,99}}{{100}} = 3,749625$
Muốn tìm mốt số khi biết $m\% $ của số đó là $b$, ta tính: $b:\dfrac{m}{{100}}$
Ví dụ:
Số có giá trị $2,5\% $ bằng $200$ là số: $200:\dfrac{{2,5}}{{100}} = 8\,000$
Tỉ số phần trăm thường được sử dụng trong đời sống để giải quyết một số bài toán như:- Mua bán hàng ngày
- Lãi suất tín dụng
- Thành phần các chất hóa học.
Phân số là một khái niệm toán học cơ bản, xuất hiện từ rất sớm trong chương trình học. Hiểu rõ về phân số là nền tảng quan trọng để học tốt các môn học khác như Đại số, Hình học và các ứng dụng thực tế.
Một phân số là một biểu thức toán học được viết dưới dạng a/b, trong đó:
Phân số biểu thị một phần của một đơn vị hoặc một tập hợp.
Có ba loại phân số chính:
Các phép toán cơ bản trên phân số bao gồm:
Để cộng hoặc trừ các phân số, ta cần quy đồng mẫu số. Sau khi quy đồng, ta cộng hoặc trừ các tử số và giữ nguyên mẫu số.
Ví dụ: Tính 1/2 + 1/3
Quy đồng mẫu số: 1/2 = 3/6 và 1/3 = 2/6
Cộng hai phân số: 3/6 + 2/6 = 5/6
Để nhân hai phân số, ta nhân các tử số với nhau và nhân các mẫu số với nhau.
Để chia hai phân số, ta nhân phân số thứ nhất với nghịch đảo của phân số thứ hai.
Ví dụ: Tính 2/3 * 1/4
Nhân hai phân số: (2 * 1) / (3 * 4) = 2/12 = 1/6
Phân số được sử dụng rộng rãi trong cuộc sống hàng ngày, ví dụ:
Để nắm vững kiến thức về phân số, các em cần luyện tập thường xuyên. Dưới đây là một số bài tập để các em tham khảo:
Lý thuyết về phân số là một phần quan trọng trong chương trình Toán 6. Việc hiểu rõ các khái niệm và phép toán trên phân số sẽ giúp các em học tốt môn Toán và ứng dụng kiến thức vào thực tế.
Chúc các em học tập tốt!