Chào mừng các em học sinh đến với bài học về Lý thuyết Số thập phân trong chương trình Toán 6 Cánh diều. Đây là một phần kiến thức quan trọng, đặt nền móng cho các khái niệm toán học phức tạp hơn ở các lớp trên.
Tại giaitoan.edu.vn, chúng tôi cung cấp bài giảng chi tiết, dễ hiểu cùng với các bài tập thực hành đa dạng, giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán liên quan đến số thập phân.
Lý thuyết Số thập phân Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu
1. Số thập phân
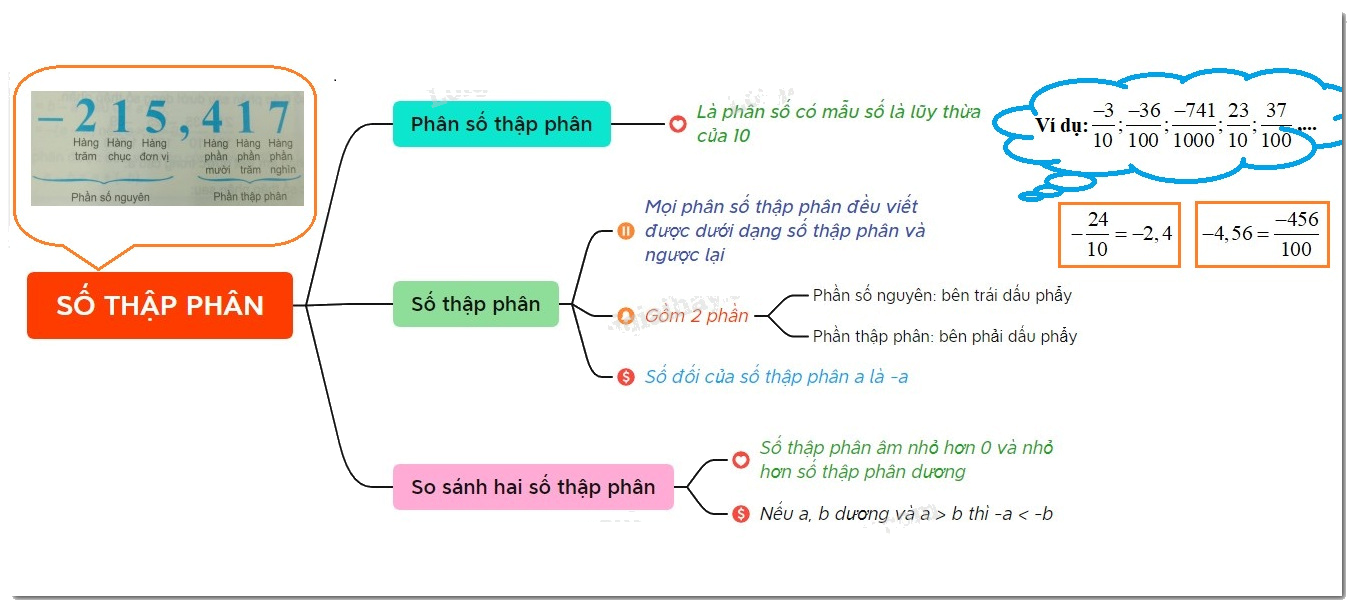
*Phân số thập phân là phân số có mẫu là lũy thừa của 10 với tử số nguyên
*Phân số thập phân có thể viết được dưới dạng số thập phân
*Số thập phân gồm 2 phần:
+ Phần số nguyên được viết bên trái dấu phẩy;
+ Phần thập phân được viết bên phải dấu phẩy
Hai số thập phân gọi là đối nhau khi chúng biểu diễn hai phân số thập phân đối nhau.
Ví dụ:
Số đối của $ - 1,5$ là $1,5$.
Số đối của $24,3$ là $ - 24,3$
2. So sánh các số thập phân
a) So sánh 2 số thập phân
Cũng như số nguyên, trong 2 số thập phân khác nhau luôn có một số lớn hơn số kia
*Nếu số thập phân a nhỏ hơn số thập phân b thì ta viết a< b hay b>a
*Số thập phân lớn hơn 0 gọi là số thập phân dương
*Số thập phân nhỏ hơn 0 gọi là số thập phân âm
b) Cách so sánh 2 số thập phân
* So sánh 2 số thập phân khác dấu: Số thập phân âm luôn nhỏ hơn số thập phân dương
* So sánh 2 số thập phân dương:
Bước 1: So sánh phần số nguyên của 2 số thập phân đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn
Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng( sau dấu ","), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữu số đó lớn hơn
* So sánh 2 số thập phân âm:
Nếu a< b thì -a> -b
Ví dụ:
a) $2,34 < 5,21$
b) Do $2,3 > 1,5$ nên $ - 2,3 < - 1,5$.
Chú ý:
Nếu $a < b$ và $b < c$ thì $a < c$.
Số thập phân là một phần quan trọng trong chương trình Toán 6, giúp học sinh làm quen với việc biểu diễn các số không nguyên bằng phần thập phân. Hiểu rõ lý thuyết số thập phân là bước đệm quan trọng để học sinh tiếp cận các phép toán phức tạp hơn như cộng, trừ, nhân, chia số thập phân.
Số thập phân là cách biểu diễn các số không nguyên bằng cách sử dụng dấu phẩy (,) để phân tách phần nguyên và phần thập phân. Ví dụ: 3,5; 0,75; 12,01 là các số thập phân.
Một số thập phân có thể được phân tích thành tổng của các phân số thập phân. Ví dụ:
3,5 = 3 + 0,5 = 3 + 5/10
0,75 = 0 + 0,75 = 0 + 75/100
Để so sánh hai số thập phân, ta thực hiện theo các bước sau:
Ví dụ: 3,5 > 3,2; 0,75 < 0,8; 12,01 = 12,01
Để biểu diễn một số thập phân trên trục số, ta thực hiện theo các bước sau:
Làm tròn số thập phân là việc thay thế số thập phân bằng một số thập phân gần nhất với một số chữ số thập phân nhất định.
Ví dụ: Làm tròn số 3,14159 đến hai chữ số thập phân ta được 3,14.
Các phép toán cộng, trừ, nhân, chia số thập phân được thực hiện tương tự như các phép toán với số nguyên, nhưng cần chú ý đến việc đặt dấu phẩy và căn chỉnh các chữ số thập phân.
Số thập phân được ứng dụng rộng rãi trong đời sống hàng ngày, ví dụ như:
Để củng cố kiến thức về lý thuyết số thập phân, các em có thể thực hành giải các bài tập sau:
Lý thuyết Số thập phân Toán 6 Cánh diều là một phần kiến thức cơ bản và quan trọng. Việc nắm vững lý thuyết này sẽ giúp các em học tốt môn Toán và ứng dụng vào thực tế một cách hiệu quả. Chúc các em học tập tốt!