Bài 2.30 trang 37 sách bài tập Toán 6 Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các phép tính với số nguyên. Bài giải chi tiết dưới đây sẽ giúp các em hiểu rõ phương pháp và cách giải bài tập này.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách bài tập Toán 6 Kết nối tri thức với cuộc sống.
Cho 6 hình vuông đơn vị, ta có hai cách xếp chúng để tạo thành các hình chữ nhật như hình dưới đây: a) Nếu cho 7 hình vuông đơn vị thì ta có mấy cách xếp chúng thành các hình chữ nhật? b) Nếu cho 12 hình vuông đơn vị thì ta có mấy cách xếp chúng thành các hình chữ nhật? c) Cho n hình vuông đơn vị (n > 1). Với những số n nào thì ta chỉ có một cách xếp chúng thành hình chữ nhật? Với những số n nào thì ta có nhiều hơn một cách xếp chúng thành hình chữ nhật?
Đề bài
Cho 6 hình vuông đơn vị, ta có hai cách xếp chúng để tạo thành các hình chữ nhật như hình dưới đây:
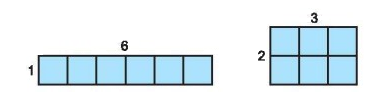
a) Nếu cho 7 hình vuông đơn vị thì ta có mấy cách xếp chúng thành các hình chữ nhật?
b) Nếu cho 12 hình vuông đơn vị thì ta có mấy cách xếp chúng thành các hình chữ nhật?
c) Cho n hình vuông đơn vị (n > 1). Với những số n nào thì ta chỉ có một cách xếp chúng thành hình chữ nhật? Với những số n nào thì ta có nhiều hơn một cách xếp chúng thành hình chữ nhật?
Phương pháp giải - Xem chi tiết
+Số hình vuông đơn vị bằng diện tích của hình chữ nhật xếp được. Do đó, ta cần tìm các bộ gồm 2 số có tích là số hình vuông
+Có bao nhiêu bộ số thì có bấy nhiêu cách xếp hình chữ nhật
Lời giải chi tiết
a) Ta có 7 = 7. 1
Do vậy ta có 1 cách xếp chúng thành hình chữ nhật.
Vậy ta xếp 1 hàng 7 hình vuông đơn vị
b) Ta có 12 = 12. 1 = 6. 2 = 4. 3
Do vậy ta có 3 cách xếp chúng thành hình chữ nhật.: Xếp 1 hàng 12 hình vuông đơn vị; 2 hàng mỗi hàng có 6 hình vuông đơn vị hoặc 3 hàng có 4 hình vuông đơn vị.
c) +Nếu n là số nguyên tố, ta chỉ có một cách xếp chúng thành hình chữ nhật vì n = n. 1
Khi đó ta xếp 1 hàng n hình vuông đơn vị.
+ Nếu n là hợp số thì n có nhiều hơn 1 cách phân tích thành tích của các số nên có nhiều hơn 1 cách sắp xếp chúng thành hình chữ nhật.
Vậy khi n là số nguyên tố, ta chỉ có một cách xếp chúng thành hình chữ nhật. Khi n là hợp số thì n có nhiều hơn 1 cách sắp xếp chúng thành hình chữ nhật.
Bài 2.30 trang 37 sách bài tập Toán 6 Kết nối tri thức với cuộc sống yêu cầu học sinh thực hiện các phép tính cộng, trừ, nhân, chia số nguyên. Để giải bài tập này một cách chính xác, học sinh cần nắm vững các quy tắc về dấu của số nguyên và thứ tự thực hiện các phép tính.
Bài tập 2.30 bao gồm một loạt các biểu thức số học, yêu cầu học sinh tính giá trị của chúng. Các biểu thức này có thể chứa các số nguyên dương, số nguyên âm, và các phép tính cộng, trừ, nhân, chia.
Ví dụ 1: Tính giá trị của biểu thức: 5 + (-3)
Giải:
5 + (-3) = 5 - 3 = 2
Ví dụ 2: Tính giá trị của biểu thức: (-4) x 2
Giải:
(-4) x 2 = -8
Để củng cố kiến thức và kỹ năng giải bài tập về số nguyên, học sinh có thể luyện tập thêm với các bài tập tương tự trong sách bài tập Toán 6 Kết nối tri thức với cuộc sống hoặc trên các trang web học toán online.
Kiến thức về số nguyên có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như:
Bài 2.30 trang 37 sách bài tập Toán 6 Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh nắm vững kiến thức về số nguyên và rèn luyện kỹ năng giải toán. Bằng cách nắm vững các quy tắc và phương pháp giải, học sinh có thể tự tin giải quyết các bài tập tương tự và ứng dụng kiến thức vào thực tế.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải Bài 2.30 trang 37 sách bài tập Toán 6 Kết nối tri thức với cuộc sống. Chúc các em học tập tốt!