Bài 6.9 trang 6 sách bài tập Toán 6 Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các phép tính với số nguyên. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để thực hiện các phép cộng, trừ, nhân, chia số nguyên một cách chính xác.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 6.9 trang 6, giúp các em học sinh nắm vững phương pháp giải và tự tin làm bài tập.
Tần số của các nốt nhạc tính theo đơn vị Hertz (Hz) được cho như sau: Em hãy viết phân số thể hiện tỉ số giữa tần số nốt Đô (C) và nốt Mi (E), rồi rút gọn về phân số tối giản.
Đề bài
Tần số của các nốt nhạc tính theo đơn vị Hertz (Hz) được cho như sau:
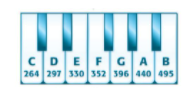
Em hãy viết phân số thể hiện tỉ số giữa tần số nốt Đô (C) và nốt Mi (E), rồi rút gọn về phân số tối giản.
Phương pháp giải - Xem chi tiết
Tần số nốt Đô là tử số, tần số nốt Mi là mẫu số của phân số
Lời giải chi tiết
Phân số thể hiện tỉ số giữa tần số nốt Đô (C) và nốt Mi (E) là:
\(\frac{{264}}{{330}} = \frac{{264:66}}{{330:66}} = \frac{4}{5}\)
Bài 6.9 trang 6 sách bài tập Toán 6 Kết nối tri thức với cuộc sống yêu cầu học sinh thực hiện các phép tính với số nguyên, bao gồm cộng, trừ, nhân, chia. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các quy tắc về dấu của số nguyên và thứ tự thực hiện các phép tính.
Trước khi bắt đầu giải bài tập, học sinh cần đọc kỹ đề bài để hiểu rõ yêu cầu. Đề bài thường yêu cầu tính giá trị của một biểu thức hoặc giải một bài toán thực tế liên quan đến số nguyên. Việc phân tích đề bài giúp học sinh xác định được các thông tin cần thiết và lựa chọn phương pháp giải phù hợp.
Quy tắc dấu của số nguyên là một kiến thức cơ bản mà học sinh cần nắm vững để giải các bài tập về số nguyên. Cụ thể:
Để đảm bảo tính chính xác của kết quả, học sinh cần thực hiện các phép tính theo đúng thứ tự sau:
Giả sử đề bài yêu cầu tính giá trị của biểu thức: (-5) + 3 - (-2) * 4
Giải:
(-5) + 3 - (-2) * 4 = (-5) + 3 + 8 = -2 + 8 = 6
Vậy, giá trị của biểu thức là 6.
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về số nguyên, học sinh có thể thực hiện các bài tập sau:
Để giải bài tập về số nguyên một cách hiệu quả, học sinh nên:
Số nguyên được ứng dụng rộng rãi trong thực tế, ví dụ như:
Việc hiểu rõ về số nguyên và các phép tính với số nguyên giúp học sinh ứng dụng kiến thức vào giải quyết các bài toán thực tế một cách dễ dàng.
Bài 6.9 trang 6 sách bài tập Toán 6 Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về số nguyên. Bằng cách nắm vững các quy tắc và phương pháp giải, học sinh có thể tự tin giải quyết các bài tập tương tự và ứng dụng kiến thức vào thực tế.