Bài 5 trang 92 sách bài tập Toán 6 Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các phép tính với số nguyên. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho Bài 5 trang 92, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Trên một trục số gốc O, hai điểm A và B lần lượt biểu diễn hai số nguyên a và b. a) Hãy tính khoảng cách AB trong mỗi trường hợp sau đây: ·a = 3 và b = 7; ·a = -3 và b = 7; ·a = -7 và b = -3; b) Tại sao có thể kết luận rằng ta luôn có AB = b - a nếu a < b. HD:Với mọi trường hợp sau, hāy vẽ hình minh họa (trên trục số nằm ngang với chiều dương từ trái sang phải) và chú ý rằng điểm biểu diễn số nguyên âm nằm cách gốc O một khoảng bằng -a (chằng hạn điểm -3 nằm cách gốc O một khoảng bằng 3 =-(-
Đề bài
Trên một trục số gốc O, hai điểm A và B lần lượt biểu diễn hai số nguyên a và b.
a) Hãy tính khoảng cách AB trong mỗi trường hợp sau đây:
·a = 3 và b = 7;
·a = -3 và b = 7;
·a = -7 và b = -3;
b) Tại sao có thể kết luận rằng ta luôn có AB = b - a nếu a < b.
HD:Với mọi trường hợp sau, hāy vẽ hình minh họa (trên trục số nằm ngang với chiều dương từ trái sang phải) và chú ý rằng điểm biểu diễn số nguyên âm nằm cách gốc O một khoảng bằng -a (chằng hạn điểm -3 nằm cách gốc O một khoảng bằng 3 =-(-3):
·Điểm O trùng với một trong hai điểm A và B.
·Điểm O nằm giữa hai điểm A và B
·Điểm O nằm trưóc (bên phải) cả hai điểm A và B
· Điểm O nằm sau (bên trái) cả hai điểm A và B.
Phương pháp giải - Xem chi tiết
Biểu diễn các số trên trục số
Lời giải chi tiết
a)
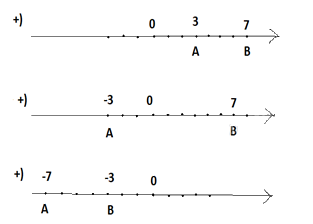
+ Với a = 3 và b = 7 thì AB = 7 – 3 = 4
+ Với a = -3 và b = 7 thì AB = 7 – (-3) = 11
+ Với a = -3 và b = -7 thì AB = (-3) – (-7) = 4
b) Ta xét các trường hợp sau:
+ Điểm O trùng điểm A: Khi đó, a = 0 nên AB = OB = b = b – 0 = b – a
+ Điểm O trùng điểm B . Khi đó, b = 0, mà a < 0 nên AB = AO = OA = -a = 0 – a = b – a
+ Điểm O nằm giữa A và B. Khi đó, a < 0 < b
Vì A biểu diễn số nguyên âm nên OA = -a; B biểu diễn số nguyên dương nên OB = b.
Ta có: O nằm giữa A và B nên AB = OB + OA = b + (-a) = b – a
+ Điểm A nằm giữa O và B:
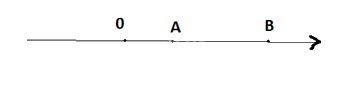
Khi đó, A, B đều biểu diễn số nguyên dương nên OA = a, OB = b
Ta có A nằm giữa O và B nên AO + AB = OB nên AB = OB – AO = b – a
+ Điểm B nằm giữa A và O
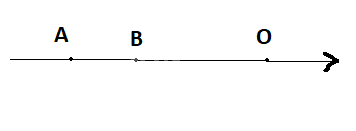
Khi đó, A, B đều biểu diễn số nguyên âm nên OA = -a ; OB = -b
Ta có B nằm giữa A và O nên AB + BO = AO nên AB =AO – BO = -a – (-b) = b –a .
Vậy ta có thể kết luận rằng ta luôn có AB = b - a nếu a < b.
Bài 5 trang 92 sách bài tập Toán 6 Kết nối tri thức với cuộc sống tập trung vào việc vận dụng các quy tắc cộng, trừ, nhân, chia số nguyên trong các bài toán thực tế. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về số nguyên, bao gồm:
Dưới đây là hướng dẫn chi tiết giải Bài 5 trang 92 sách bài tập Toán 6 Kết nối tri thức với cuộc sống:
Trước khi bắt đầu giải, hãy đọc kỹ đề bài và tóm tắt các thông tin quan trọng. Xác định rõ các số liệu, các phép tính cần thực hiện và yêu cầu của bài toán.
Áp dụng các quy tắc cộng, trừ, nhân, chia số nguyên để giải quyết bài toán. Lưu ý thực hiện các phép tính theo đúng thứ tự ưu tiên (nhân, chia trước; cộng, trừ sau). Kiểm tra lại kết quả để đảm bảo tính chính xác.
Để giúp các em học sinh hiểu rõ hơn, chúng ta sẽ cùng xem xét một ví dụ minh họa:
Ví dụ: Tính (-5) + 3 - (-2) * 4
Giải:
Vậy, kết quả của phép tính là -10.
Để củng cố kiến thức và kỹ năng giải toán, các em học sinh nên luyện tập thêm với các bài tập tương tự. Dưới đây là một số bài tập luyện tập:
Lời khuyên:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải Bài 5 trang 92 sách bài tập Toán 6 Kết nối tri thức với cuộc sống và đạt kết quả tốt trong môn Toán.
Ngoài việc giải Bài 5 trang 92, các em học sinh có thể tìm hiểu thêm về các ứng dụng của số nguyên trong thực tế. Ví dụ, số nguyên được sử dụng để biểu diễn nhiệt độ, độ cao, số tiền nợ, v.v. Việc hiểu rõ các ứng dụng này sẽ giúp các em học sinh thấy được tính hữu ích của môn Toán trong cuộc sống.
Để học tập và ôn luyện môn Toán hiệu quả, các em học sinh có thể tham khảo các nguồn tài liệu sau:
Chúc các em học tập tốt!