Bài 8.25 trang 46 sách bài tập Toán 6 Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các phép tính với số nguyên. Bài giải chi tiết dưới đây sẽ giúp các em hiểu rõ phương pháp và tự tin giải các bài tập tương tự.
giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và đạt kết quả tốt trong môn Toán.
Người ta coi mỗi hình là một tập hợp điểm. Nếu P và Q là hai điểm phân biệt đã cho thì mỗi tập hợp điểm sau đây là hình nào? Hãy vẽ hình đó. G = {X| X là điểm P, hoặc X là điểm nằm khác phía với Q đối với P}
Đề bài
Người ta coi mỗi hình là một tập hợp điểm. Nếu P và Q là hai điểm phân biệt đã cho thì mỗi tập hợp điểm sau đây là hình nào? Hãy vẽ hình đó.
G = {X| X là điểm P, hoặc X là điểm nằm khác phía với Q đối với P}
Phương pháp giải - Xem chi tiết
Vẽ hình
Lời giải chi tiết
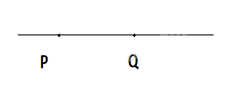
Tập hợp G là tia đối của tia PQ.
Bài 8.25 trang 46 sách bài tập Toán 6 Kết nối tri thức với cuộc sống yêu cầu học sinh thực hiện các phép tính với số nguyên, bao gồm cộng, trừ, nhân, chia và sử dụng dấu ngoặc để thay đổi thứ tự thực hiện các phép tính. Để giải bài tập này một cách chính xác, học sinh cần nắm vững các quy tắc về thứ tự thực hiện các phép tính và các quy tắc về dấu của số nguyên.
Bài tập 8.25 bao gồm một loạt các biểu thức số học khác nhau. Các biểu thức này có thể chứa các số nguyên dương, số nguyên âm, và các phép toán cộng, trừ, nhân, chia. Một số biểu thức có thể chứa dấu ngoặc, đòi hỏi học sinh phải thực hiện các phép tính trong ngoặc trước.
Để giải bài tập 8.25, học sinh có thể áp dụng các bước sau:
Giả sử một biểu thức trong bài tập 8.25 là: (-2) + 3 * (-4) - 5
Để giải biểu thức này, ta thực hiện các bước sau:
3 * (-4) = -12(-2) + (-12) - 5(-2) + (-12) = -14-14 - 5 = -19Vậy, kết quả của biểu thức (-2) + 3 * (-4) - 5 là -19.
Để nắm vững kiến thức và kỹ năng giải bài tập về các phép tính với số nguyên, học sinh nên luyện tập thêm với các bài tập tương tự. giaitoan.edu.vn cung cấp một loạt các bài tập luyện tập khác nhau, giúp học sinh rèn luyện kỹ năng và tự tin giải các bài tập khó hơn.
Kiến thức về số nguyên là nền tảng quan trọng cho việc học toán ở các lớp trên. Việc nắm vững kiến thức về số nguyên giúp học sinh hiểu rõ hơn về các khái niệm toán học khác, chẳng hạn như đại số, hình học, và giải tích. Do đó, học sinh nên dành thời gian để học tập và luyện tập về số nguyên một cách nghiêm túc.
Kiến thức về số nguyên không chỉ quan trọng trong môn toán mà còn có nhiều ứng dụng trong thực tế. Ví dụ, số nguyên được sử dụng để biểu diễn nhiệt độ, độ cao, và các khoản nợ. Do đó, việc nắm vững kiến thức về số nguyên giúp học sinh hiểu rõ hơn về thế giới xung quanh.
Khi giải bài tập về số nguyên, học sinh nên:
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài tập 8.25 trang 46 sách bài tập Toán 6 Kết nối tri thức với cuộc sống và đạt kết quả tốt trong môn Toán.