Bài 8.45 trang 54 sách bài tập Toán 6 Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các phép tính với số nguyên. Bài giải chi tiết dưới đây sẽ giúp các em hiểu rõ phương pháp và cách giải bài tập này.
giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Vẽ góc xOy không bẹt và điểm M là điểm trong của góc đó. Qua M, vẽ một đường thẳng cắt hai cạnh của góc tại A và B sao cho A thuộc Ox và B thuộc Oy. Hỏi trong ba điểm A, B và M, điểm nào nằm giữa hai điểm còn lại?
Đề bài
Vẽ góc xOy không bẹt và điểm M là điểm trong của góc đó. Qua M, vẽ một đường thẳng cắt hai cạnh của góc tại A và B sao cho A \( \in \) Ox và B \( \in \) Oy. Hỏi trong ba điểm A, B và M, điểm nào nằm giữa hai điểm còn lại?
Phương pháp giải - Xem chi tiết
Vẽ theo mô tả
Lời giải chi tiết
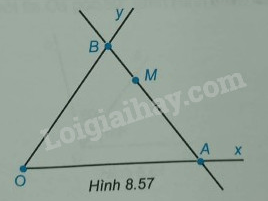
Điểm M nằm giữa hai điểm còn lại.
Bài 8.45 yêu cầu chúng ta thực hiện các phép tính với số nguyên, bao gồm cộng, trừ, nhân, chia và sử dụng dấu ngoặc để đảm bảo thứ tự thực hiện các phép toán. Để giải bài tập này một cách chính xác, chúng ta cần nắm vững các quy tắc về thứ tự thực hiện các phép toán và các quy tắc về dấu của số nguyên.
Bài tập 8.45 thường bao gồm các biểu thức số học phức tạp, đòi hỏi học sinh phải phân tích và áp dụng đúng các quy tắc toán học. Ví dụ, một biểu thức có thể có dạng:
Để giải các biểu thức này, chúng ta thực hiện theo các bước sau:
Ví dụ 1: Tính giá trị của biểu thức (12 + 3) x 4 - 15 : 3
Giải:
Ví dụ 2: Tính giá trị của biểu thức -5 x (8 - 2) + 10 : 2
Giải:
Số nguyên bao gồm các số dương, số âm và số 0. Các số nguyên được sử dụng rộng rãi trong toán học và các lĩnh vực khác của đời sống. Để hiểu rõ hơn về số nguyên, chúng ta cần nắm vững các khái niệm sau:
Để củng cố kiến thức và kỹ năng giải bài tập về số nguyên, các em có thể luyện tập thêm các bài tập tương tự sau:
Kết luận: Bài 8.45 trang 54 sách bài tập Toán 6 Kết nối tri thức với cuộc sống là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về các phép tính với số nguyên. Bằng cách nắm vững các quy tắc và thực hành thường xuyên, các em sẽ tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.