Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 6. Bài viết này sẽ hướng dẫn bạn giải bài 30 trang 95 sách bài tập Toán 6 – Cánh Diều Tập 2 một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập mới. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn nắm vững kiến thức và tự tin hơn trong học tập.
a) Vẽ đoạn thẳng AB có độ dài 8 cm và trung điểm C của đoạn thẳng đó. b) Vẽ các điểm P, Q lần lượt là trung điểm của các đoạn thẳng AC và CB c) Tính độ dài các đoạn thẳng AP, QB và PQ.
Đề bài
a) Vẽ đoạn thẳng AB có độ dài 8 cm và trung điểm C của đoạn thẳng đó.
b) Vẽ các điểm P, Q lần lượt là trung điểm của các đoạn thẳng AC và CB
c) Tính độ dài các đoạn thẳng AP, QB và PQ.
Phương pháp giải - Xem chi tiết
Trung điểm O của đoạn thẳng AB là điểm nằm giữa A và B sao cho \(OA = OB\)
Nếu O là trung điểm của đoạn thẳng AB thì \(OA = OB = \frac{{AB}}{2}\)
Lời giải chi tiết
a) Đoạn thẳng AB có độ dài 8 cm và C là trung điểm của đoạn thẳng đó.
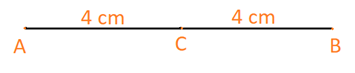
Vì C là trung điểm AB nên \(CA = CB = \frac{{AB}}{2} = \frac{8}{2}= 4\,cm\)
b) P, Q lần lượt là trung điểm của các đoạn thẳng AC và CB
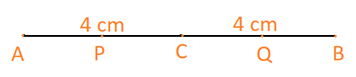
c) Ta có:
P là trung điểm AC nên \(PA = PC = \frac{{AC}}{2} = \frac{4}{2}= 2\,cm\)
Q là trung điểm BC nên \(QB = QC = \frac{{BC}}{2} = \frac{4}{2}=2\,cm\)
Mà: \(PQ = PC + CQ\)(vì C nằm giữa P và Q)
\( \Rightarrow PQ = 2 + 2 = 4\,(cm)\)
Vậy \(AP = 2\,cm;\;QB = 2\,cm;\;PQ = 4\,cm\)
Bài 30 trang 95 sách bài tập Toán 6 – Cánh Diều Tập 2 thuộc chương trình học Toán 6, tập trung vào việc ôn tập và củng cố kiến thức về các phép tính với số nguyên, phân số, và các bài toán thực tế liên quan. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các vấn đề cụ thể, rèn luyện tư duy logic và kỹ năng giải toán.
Bài 30 bao gồm các dạng bài tập sau:
Để giải bài tập 1, bạn cần nắm vững các quy tắc về thứ tự thực hiện các phép tính: trong ngoặc trước, ngoài ngoặc sau; nhân chia trước, cộng trừ sau. Ngoài ra, cần chú ý đến dấu của các số nguyên và phân số.
Ví dụ:
Tính: 2 + 3 x 4 - 5
Khi giải bài toán thực tế, bạn cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yếu tố cần tìm. Sau đó, vận dụng các kiến thức đã học để lập phương trình hoặc biểu thức toán học phù hợp, và giải để tìm ra kết quả.
Ví dụ:
Một cửa hàng bán được 25 kg gạo với giá 15.000 đồng/kg. Hỏi cửa hàng thu được bao nhiêu tiền?
Giải:
Số tiền cửa hàng thu được là: 25 x 15.000 = 375.000 đồng
Vậy, cửa hàng thu được 375.000 đồng.
Để tìm x trong các phương trình đơn giản, bạn cần thực hiện các phép biến đổi tương đương để đưa x về một vế của phương trình. Sau đó, thực hiện các phép tính để tìm ra giá trị của x.
Ví dụ:
Tìm x: x + 5 = 10
Giải:
x = 10 - 5
x = 5
Vậy, x = 5
Bài 30 trang 95 sách bài tập Toán 6 – Cánh Diều Tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong việc giải bài tập và đạt kết quả tốt trong học tập.