Chào mừng các em học sinh đến với lời giải chi tiết Bài 8 trang 106 sách bài tập Toán 6 Cánh Diều. Bài viết này sẽ cung cấp đáp án, hướng dẫn giải bài tập một cách dễ hiểu, giúp các em tự tin hơn trong quá trình học tập môn Toán.
giaitoan.edu.vn luôn đồng hành cùng các em học sinh, cung cấp tài liệu học tập chất lượng và hỗ trợ giải đáp mọi thắc mắc.
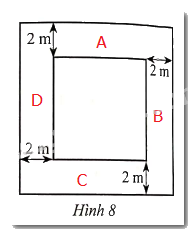
Nhà trường mở rộng một khu vườn có dạng hình vuông vê cả bốn phía, mỗi phía thêm 2 m, nên diện tích tăng thêm 80 m2 (Hình 8). Độ dài mỗi cạnh sau khi mở rộng là bao nhiêu mét?
Đề bài
Nhà trường mở rộng một khu vườn có dạng hình vuông về cả bốn phía, mỗi phía thêm 2 m, nên diện tích tăng thêm 80 m2 (Hình 8). Độ dài mỗi cạnh sau khi mở rộng là bao nhiêu mét?

Phương pháp giải - Xem chi tiết
Gọi a là chiều dài cạnh của khu vườn
Biểu diễn diện tích tăng thêm của khu vườn theo a
Tìm a.
Lời giải chi tiết
Gọi a (m) là chiều dài cạnh của khu vườn ( a > 0 )
Diện tích tăng thêm là tổng diện tích của 4 mảnh A,B,C,D. Mỗi mảnh là một hình chữ nhật có chiều dài a + 2 (cm), chiều rộng là 2 (cm). Do đó:
Diện tích tăng thêm của khu vườn là 4. 2. (a+2). Theo đề bài ta có:
4. 2. (a+2) = 80
8. (a+2) = 80
a + 2 = 80 : 8
a + 2 = 10
a = 8 (Thỏa mãn)
Vậy độ dài mỗi cạnh sau khi mở rộng là: a + 2 + 2 = 8 + 2 + 2 = 12 (m)
Bài 8 trang 106 sách bài tập Toán 6 Cánh Diều thuộc chương trình học Toán 6, tập trung vào việc ôn tập và củng cố kiến thức về các phép tính với số tự nhiên, các khái niệm về bội và ước số. Việc nắm vững kiến thức này là nền tảng quan trọng cho các bài học tiếp theo.
Bài 8 bao gồm các dạng bài tập khác nhau, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các vấn đề thực tế. Cụ thể, bài tập thường xoay quanh các chủ đề sau:
Để giúp các em học sinh giải bài tập một cách hiệu quả, chúng tôi sẽ cung cấp hướng dẫn chi tiết cho từng câu hỏi trong bài 8 trang 106 sách bài tập Toán 6 Cánh Diều.
Để tìm BCNN của 12 và 18, ta có thể sử dụng phương pháp phân tích ra thừa số nguyên tố:
Vậy, BCNN của 12 và 18 là 36.
Để tìm UCLN của 24 và 36, ta cũng sử dụng phương pháp phân tích ra thừa số nguyên tố:
Vậy, UCLN của 24 và 36 là 12.
Để giải bài toán này, ta cần tìm UCLN của 24 và 36, vì số nhóm nhiều nhất có thể chia chính là UCLN của số học sinh nam và số học sinh nữ.
Như đã tính ở câu 2, UCLN(24, 36) = 12. Vậy, số nhóm nhiều nhất có thể chia là 12 nhóm.
Khi giải các bài tập về BCNN và UCLN, các em cần lưu ý những điều sau:
BCNN và UCLN không chỉ là kiến thức lý thuyết mà còn có nhiều ứng dụng thực tế trong đời sống. Ví dụ:
Bài 8 trang 106 sách bài tập Toán 6 Cánh Diều là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về BCNN, UCLN và các phép tính với số tự nhiên. Hy vọng với hướng dẫn chi tiết này, các em sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt.
giaitoan.edu.vn luôn sẵn sàng hỗ trợ các em trong quá trình học tập. Chúc các em học tốt!