Chào mừng các em học sinh đến với lời giải chi tiết bài 1.10 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán, cung cấp các bài giải chuẩn xác và đầy đủ.
Dùng com-pa, thước kẻ, bút, hãy vẽ lại các nét thẳng và tròn trong Hình 1.19.
Đề bài
Dùng com-pa, thước kẻ, bút, hãy vẽ lại các nét thẳng và tròn trong Hình 1.19.
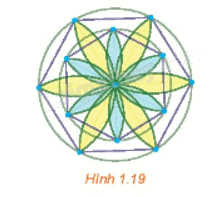
Phương pháp giải - Xem chi tiết
Có một đường thẳng chia hình thành hai phần bằng nhau mà nếu “gấp” hình theo đường thẳng thì hai phần đó “chồng khít” lên nhau. Được gọi là hình có trục đối xứng và đường thẳng là trục đối xứng của nó
Lời giải chi tiết
Sử dụng tính đối xứng trục, ta vẽ được hình:
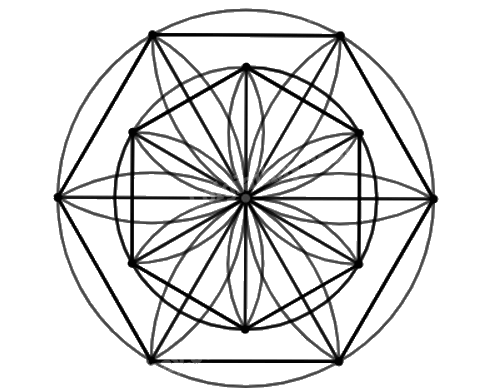
Bài 1.10 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về giới hạn của hàm số để giải quyết các bài toán thực tế. Bài tập này yêu cầu học sinh phải hiểu rõ định nghĩa giới hạn, các tính chất của giới hạn và các phương pháp tính giới hạn.
Bài 1.10 thường bao gồm các dạng bài tập sau:
Để giải quyết bài tập 1.10 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức một cách hiệu quả, học sinh cần nắm vững các phương pháp sau:
(Giả sử bài tập cụ thể là: Tính lim (x->2) (x^2 - 4) / (x - 2))
Lời giải:
Ta có:
lim (x->2) (x^2 - 4) / (x - 2) = lim (x->2) [(x - 2)(x + 2)] / (x - 2)
= lim (x->2) (x + 2)
= 2 + 2 = 4
Vậy, lim (x->2) (x^2 - 4) / (x - 2) = 4
(Giả sử bài tập cụ thể là: Tính lim (x->0) sin(x) / x)
Lời giải:
Đây là một giới hạn lượng giác cơ bản. Ta có thể sử dụng định lý giới hạn đặc biệt:
lim (x->0) sin(x) / x = 1
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về giới hạn, các em có thể tham khảo các bài tập sau:
Bài 1.10 trang 15 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về khái niệm giới hạn và các ứng dụng của nó. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày trong bài viết này, các em sẽ tự tin hơn trong quá trình học tập và giải quyết các bài toán tương tự.