Giải bài 3.22 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức

Bài 3.22 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.

Hãy cùng khám phá lời giải chi tiết và các kiến thức liên quan ngay dưới đây!

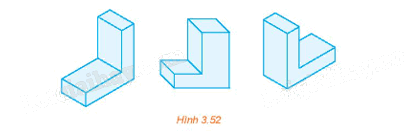
Sử dụng thước đo góc nếu cần thiết, hãy cho biết hình nào trong Hình 3.52 là hình chiếu trục đo vuông góc đều.

Đề bài

Sử dụng thước đo góc nếu cần thiết, hãy cho biết hình nào trong Hình 3.52 là hình chiếu trục đo vuông góc đều.

Giải bài 3.22 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức 1

Phương pháp giải - Xem chi tiết Giải bài 3.22 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức 2

Trong hình chiếu trục đo vuông góc đều có:

- Mặt phẳng chiếu (P) vuông góc với phương chiếu l;

- Các góc trục đo đều bằng 120^o.

- Các hệ số biến dạng đều bằng 1.

Lời giải chi tiết

Hình 3.52 thứ hai tính từ trái có các góc trục đo khác 120° nên không là hình chiếu trục đo vuông góc đều. Hình 3.52 thứ nhất và 3.52 thứ ba là hình chiếu trục đo vuông góc đều.

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải bài 3.22 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức – hành trang không thể thiếu trong chuyên mục Sách giáo khoa Toán 11 trên nền tảng môn toán. Bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải bài 3.22 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết

Bài 3.22 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh giải một bài toán liên quan đến việc tìm cực trị của hàm số. Để giải bài toán này, chúng ta cần nắm vững các kiến thức về đạo hàm, điều kiện cần và đủ để hàm số đạt cực trị, và các bước giải bài toán cực trị.

I. Đề bài

(Đề bài bài 3.22 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức được chèn vào đây)

II. Phương pháp giải

Để giải bài toán này, chúng ta thực hiện theo các bước sau:

Tính đạo hàm cấp một (f'(x)) của hàm số.
Tìm các điểm dừng của hàm số bằng cách giải phương trình f'(x) = 0.
Xác định dấu của đạo hàm cấp hai (f''(x)) tại các điểm dừng.
Kết luận về cực trị của hàm số dựa vào dấu của f''(x):
- Nếu f''(x) > 0 thì hàm số đạt cực tiểu tại điểm đó.
- Nếu f''(x) < 0 thì hàm số đạt cực đại tại điểm đó.
- Nếu f''(x) = 0 thì cần xét thêm đạo hàm cấp ba để xác định.

III. Lời giải chi tiết

(Lời giải chi tiết bài 3.22 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức được chèn vào đây, bao gồm các bước tính toán cụ thể, giải thích rõ ràng và kết luận chính xác.)

IV. Ví dụ minh họa

Để hiểu rõ hơn về phương pháp giải, chúng ta cùng xét một ví dụ minh họa:

(Ví dụ minh họa về bài toán cực trị được chèn vào đây, với lời giải chi tiết và giải thích rõ ràng.)

V. Bài tập tương tự

Để rèn luyện kỹ năng giải bài toán cực trị, bạn có thể thử giải các bài tập tương tự sau:

Bài 1: Tìm cực trị của hàm số y = x^3 - 3x^2 + 2.
Bài 2: Tìm cực trị của hàm số y = x^4 - 4x^2 + 3.
Bài 3: Tìm cực trị của hàm số y = (x-1)/(x+1).

VI. Lưu ý quan trọng

Khi giải bài toán cực trị, bạn cần lưu ý những điều sau:

Kiểm tra kỹ điều kiện xác định của hàm số.
Tính đạo hàm chính xác.
Xác định đúng dấu của đạo hàm cấp hai.
Kết luận chính xác về cực trị của hàm số.

VII. Tổng kết

Bài 3.22 trang 81 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, bạn đã có thể tự tin giải bài toán này và các bài toán tương tự.

Giaitoan.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán. Chúc bạn học tập tốt!