Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn cách giải bài 2.6 trang 40 trong Chuyên đề học tập Toán 11 Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
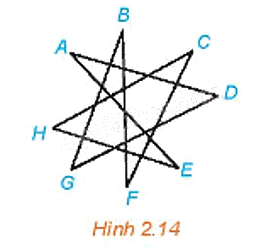
Cho đồ thị G như Hình 2.14.
Đề bài
Cho đồ thị G như Hình 2.14.
a) Tìm một đường đi từ đỉnh A đến đỉnh B.
b) G có liên thông không?
c) Trong G có chu trình sơ cấp nào không?
Phương pháp giải - Xem chi tiết
Một đồ thị được gọi là liên thông nếu hai đỉnh bất kì của đồ thị đều được nối với nhau bằng một đường đi.
Lời giải chi tiết
a) Một đường đi từ đỉnh A đến đỉnh B là: ADGB.
b) Ta thấy hai đỉnh bất kì của đồ thị đều liên thông (tức là đều có đường đi nối chúng), nên G liên thông.
c) Chu trình sơ cấp trong G là: AEHCFBGDA.
Bài 2.6 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức thuộc chương trình học Toán 11, tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Bài tập 2.6 thường bao gồm các dạng bài sau:
Để giải quyết bài tập 2.6 trang 40 một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
Ví dụ: Cho hàm số y = x3 - 3x2 + 2. Tìm cực đại và cực tiểu của hàm số.
Giải:
Để củng cố kiến thức và kỹ năng giải bài tập 2.6 trang 40, bạn có thể luyện tập thêm với các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Ngoài ra, bạn cũng có thể tìm kiếm các bài giải trực tuyến trên các trang web học toán uy tín như giaitoan.edu.vn.
Để học tốt môn Toán 11, bạn cần:
Bài 2.6 trang 40 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, bạn sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!