Bài 3.15 trang 79 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài giải chi tiết dưới đây sẽ cung cấp phương pháp tiếp cận và lời giải chính xác, giúp bạn hiểu rõ hơn về kiến thức và kỹ năng cần thiết.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, cùng với các bài tập tương tự để bạn có thể luyện tập và củng cố kiến thức. Hãy cùng khám phá lời giải bài 3.15 này ngay nhé!
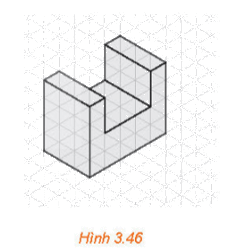
Tính thể tích của vật thể được biểu diễn trên giấy kẻ ô tam giác đều trong Hình 3.46.
Đề bài
Tính thể tích của vật thể được biểu diễn trên giấy kẻ ô tam giác đều trong Hình 3.46. Quy ước mỗi cạnh của tam giác đều có chiều dài là 1 cm.
Phương pháp giải - Xem chi tiết
Quan sát hình 3.46 để làm
Lời giải chi tiết
Ta có: Thể tích vật thể giá chữ U này bằng hiệu thể tích của hình hộp chữ nhật bao ngoài vật thể và thể tích rãnh hộp chữ nhật.
Hình hộp chữ nhật bao ngoài có chiều dài 5 cm, chiều rộng 3 cm, chiều cao 4 cm.
Suy ra, thể tích hình hộp chữ nhật bao ngoài là: 5 . 3 . 4 = 60 (cm3).
Rãnh hộp chữ nhật có chiều dài 3 cm, chiều rộng 3 cm, chiều cao 2 cm.
Suy ra, thể tích rãnh hộp chữ nhật là: 3 . 3 . 2 = 18 (cm3).
Vậy thể tích vật thể giá chữ U là: 60 – 18 = 42 (cm3).
Bài 3.15 trang 79 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến việc khảo sát hàm số. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các bước sau:
Đề bài: (Giả sử đề bài cụ thể ở đây, ví dụ: Cho hàm số y = x3 - 3x2 + 2. Khảo sát hàm số.)
Giải:
Hàm số y = x3 - 3x2 + 2 xác định trên tập số thực R.
y' = 3x2 - 6x
y'' = 6x - 6
Giải phương trình y' = 0:
3x2 - 6x = 0
3x(x - 2) = 0
=> x = 0 hoặc x = 2
Vậy hàm số có hai điểm cực trị: x1 = 0 và x2 = 2
Giải phương trình y'' = 0:
6x - 6 = 0
=> x = 1
Vậy hàm số có điểm uốn tại x = 1
Hàm số y = x3 - 3x2 + 2 có:
Đồ thị hàm số có dạng:
(Mô tả đồ thị hàm số, ví dụ: Đồ thị hàm số đi qua các điểm (0, 2), (1, 0), (2, -2). Hàm số đồng biến trên (-∞, 0) và (2, +∞), nghịch biến trên (0, 2). Hàm số lõm trên (-∞, 1) và lồi trên (1, +∞).)
Để nắm vững kiến thức về khảo sát hàm số bằng đạo hàm, bạn nên luyện tập thêm với các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo. Giaitoan.edu.vn sẽ cung cấp thêm nhiều bài tập và lời giải chi tiết để bạn có thể tự tin hơn trong quá trình học tập.
Đạo hàm không chỉ là một công cụ quan trọng trong toán học mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác như vật lý, kinh tế, kỹ thuật,... Ví dụ, đạo hàm có thể được sử dụng để tính vận tốc, gia tốc, tối ưu hóa lợi nhuận, phân tích sự thay đổi của các đại lượng,...