Bài 1.31 trang 33 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải chi tiết của bài tập này ngay dưới đây!
Cho đường thẳng d và hai điểm A, B cùng thuộc một nửa mặt phẳng bờ d.
Đề bài
Cho đường thẳng d và hai điểm A, B cùng thuộc một nửa mặt phẳng bờ d. Hai điểm E, F thay đổi trên d sao cho \(\overrightarrow {EF} \) không đổi. Xác định vị trí của hai điểm E, F để AE + BF nhỏ nhất.
Phương pháp giải - Xem chi tiết
Dựa vào kiến thức đã học về phép biến hình để làm
Lời giải chi tiết
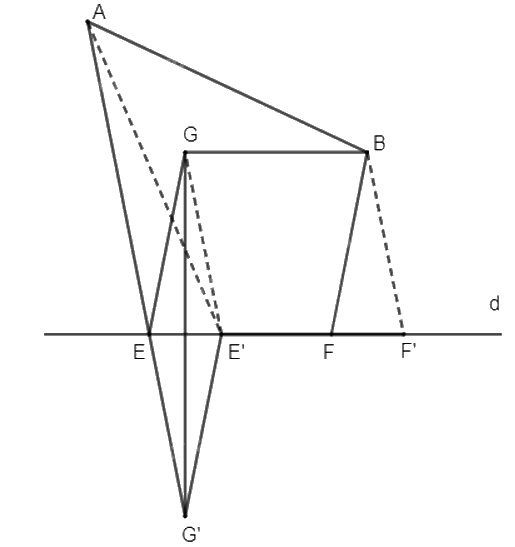
Ta có: \(\left| {\overrightarrow {EF} } \right| = m\,\,(m > 0)\) không đổi.
Đặt \(\vec u = \overrightarrow {EF\;} \left( {\vec u \ne \vec 0} \right),\,\vec u\) không đổi, khi đó \(\mid \overrightarrow u \mid = m\) không đổi.
Gọi G là ảnh của điểm B qua phép tịnh tiến theo vectơ \(\vec u\). Khi đó \(\overrightarrow {BG} = - \vec u\). Vì B cố định và \(\overrightarrow u \) không đổi nên G cố định. Gọi G' là ảnh của G qua phép đối xứng trục d thì G' cố định.
Gọi giao điểm của AG' và đường thẳng d là E, trên d lấy điểm F thỏa mãn EF = m và \(\overrightarrow {EF} = \vec u = - \overrightarrow {BG} \) hay \(\overrightarrow {EF} = \overrightarrow {GB} \). Khi đó BGEF là hình bình hành nên BF = GE.
Mà G và G' đối xứng nhau qua d nên GE = G'E. Do đó BF = GE = G'E.
Ta có: AE + BF = AE + G'E = AG' (1).
Ta có E và F như trên là hai điểm cần tìm để AE + BF nhỏ nhất.
Thật vậy, gọi E' và F' là 2 điểm trên d, khác E và F sao cho \(\overrightarrow {E'F'} = \vec u\) và \(\left| {\overrightarrow {E'F'} } \right| = \left| {\vec u} \right| = m\).
Ta có: AE' + BF' = AE' + GE' = AE' + G'E' > AG' (2) (bất đẳng thức trong tam giác AG'E').
Từ (1) và (2) suy ra AE + BF < AE' + BF'. Từ đó suy ra điều phải chứng minh.
Bài 1.31 trang 33 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để tìm cực trị của hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
Đề bài: (Giả sử đề bài cụ thể của bài 1.31 được đưa ra ở đây. Ví dụ: Tìm cực đại, cực tiểu của hàm số f(x) = x^3 - 3x^2 + 2)
Giải:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Việc giải bài 1.31 trang 33 Chuyên đề học tập Toán 11 Kết nối tri thức không chỉ giúp học sinh nắm vững kiến thức về đạo hàm mà còn là nền tảng để giải quyết các bài toán thực tế liên quan đến tối ưu hóa, tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Các ứng dụng của đạo hàm rất rộng rãi trong các lĩnh vực như kinh tế, kỹ thuật, vật lý,...
Ngoài sách giáo khoa và chuyên đề học tập, học sinh có thể tham khảo thêm các tài liệu trực tuyến, video bài giảng, và các diễn đàn học tập để nâng cao kiến thức và kỹ năng giải bài tập về đạo hàm. Giaitoan.edu.vn luôn cập nhật và cung cấp các lời giải chi tiết, dễ hiểu cho các bài tập Toán 11, giúp bạn học tập hiệu quả hơn.
Để củng cố kiến thức, bạn có thể thử giải các bài tập tương tự sau: