Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Trong chuyên đề này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục 2 trang 6, 7, 8 của sách Chuyên đề học tập Toán 11 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Trên mặt phẳng tọa độ Oxy, cho phép biến hình f biến mỗi điểm (Mleft( {x;{rm{ }}y} right)) thành điểm (M'left( {x{rm{ }} + {rm{ }}1;{rm{ }}y{rm{ }} + {rm{ }}2} right).)
Trên mặt phẳng tọa độ Oxy, cho phép biến hình f biến mỗi điểm \(M\left( {x;{\rm{ }}y} \right)\) thành điểm \(M'\left( {x{\rm{ }} + {\rm{ }}1;{\rm{ }}y{\rm{ }} + {\rm{ }}2} \right).\)
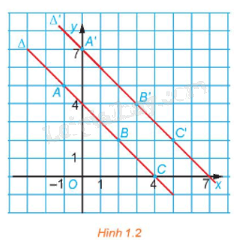
a) Xét các điểm \(A\left( {-{\rm{ }}1;{\rm{ }}5} \right),{\rm{ }}B\left( {2;{\rm{ }}2} \right),{\rm{ }}C\left( {4;{\rm{ }}0} \right)\) thuộc \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\). Xác định các ảnh của chúng qua f.
b) Chứng minh rằng nếu \(M\left( {{x_0};{\rm{ }}{y_0}} \right)\) là điểm thuộc đường thẳng \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\) thì ảnh \(M'\left( {{x_0}\; + {\rm{ }}1;{\rm{ }}{y_0}\; + {\rm{ }}2} \right)\) của nó thuộc đường thẳng \(\Delta ':{\rm{ }}x + {\rm{ }}y{\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0.\;\;\)
Phương pháp giải:
Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).
Lời giải chi tiết:
a) Ảnh của điểm A(– 1; 5) qua phép biến hình f là điểm \(A'\left( {-{\rm{ }}1{\rm{ }} + {\rm{ }}1;{\rm{ }}5{\rm{ }} + {\rm{ }}2} \right)\) hay \(A'\left( {0;{\rm{ }}7} \right).\)
Ảnh của điểm B(2; 3) qua phép biến hình f là điểm \(B'\left( {2{\rm{ }} + {\rm{ }}1;{\rm{ }}3{\rm{ }} + {\rm{ }}2} \right)\) hay \(B'\left( {3;{\rm{ }}5} \right).\)
Ảnh của điểm C(4; 0) qua phép biến hình f là điểm \(C'\left( {4{\rm{ }} + {\rm{ }}1;{\rm{ }}0{\rm{ }} + {\rm{ }}2} \right)\) hay \(C'\left( {5;{\rm{ }}2} \right).\)
b) Vì \(M\left( {{x_0};{\rm{ }}{y_0}} \right)\) thuộc \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\) nên \({x_0}\; + {\rm{ }}{y_0}\;-{\rm{ }}4{\rm{ }} = {\rm{ }}0\) hay \({x_0}\; + {\rm{ }}{y_{0\;}} = {\rm{ }}4\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow \;{x_0}\; + {\rm{ }}{y_0}\; + {\rm{ }}3{\rm{ }} = {\rm{ }}4{\rm{ }} + {\rm{ }}3}\\{ \Leftrightarrow \;\left( {{x_0}\; + {\rm{ }}1} \right){\rm{ }} + {\rm{ }}\left( {{y_{0\;}} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }}7}\\{ \Leftrightarrow \;\left( {{x_0}\; + {\rm{ }}1} \right){\rm{ }} + {\rm{ }}\left( {{y_{0\;}} + {\rm{ }}2} \right){\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0}\end{array}\)
Suy ra \(M'\left( {{x_0}\; + {\rm{ }}1;{\rm{ }}{y_0}\; + {\rm{ }}2} \right)\) thuộc đường thẳng \(\Delta ':{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0.\)
Quan sát ba tấm ảnh hoa hồng ở Hình 1.4, hãy cho biết hình nào giống ảnh của hình ở giữa qua một phép co về trục.

Phương pháp giải:
Quan sát hình vẽ để trả lời
Lời giải chi tiết:
Quan sát Hình 1.4, ta thấy hình phía bên phải hình ở giữa giống ảnh của hình ở giữa qua một phép co về trục.
Trên mặt phẳng tọa độ Oxy, cho phép biến hình f biến mỗi điểm \(M\left( {x;{\rm{ }}y} \right)\) thành điểm \(M'\left( {x{\rm{ }} + {\rm{ }}1;{\rm{ }}y{\rm{ }} + {\rm{ }}2} \right).\)
a) Xét các điểm \(A\left( {-{\rm{ }}1;{\rm{ }}5} \right),{\rm{ }}B\left( {2;{\rm{ }}2} \right),{\rm{ }}C\left( {4;{\rm{ }}0} \right)\) thuộc \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\). Xác định các ảnh của chúng qua f.
b) Chứng minh rằng nếu \(M\left( {{x_0};{\rm{ }}{y_0}} \right)\) là điểm thuộc đường thẳng \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\) thì ảnh \(M'\left( {{x_0}\; + {\rm{ }}1;{\rm{ }}{y_0}\; + {\rm{ }}2} \right)\) của nó thuộc đường thẳng \(\Delta ':{\rm{ }}x + {\rm{ }}y{\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0.\;\;\)

Phương pháp giải:
Phép biến hình f trong mặt phẳng là một quy tắc cho tương ứng với mỗi điểm M với duy nhất một điểm M’. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình f, kí hiệu \(M' = f(M)\).
Lời giải chi tiết:
a) Ảnh của điểm A(– 1; 5) qua phép biến hình f là điểm \(A'\left( {-{\rm{ }}1{\rm{ }} + {\rm{ }}1;{\rm{ }}5{\rm{ }} + {\rm{ }}2} \right)\) hay \(A'\left( {0;{\rm{ }}7} \right).\)
Ảnh của điểm B(2; 3) qua phép biến hình f là điểm \(B'\left( {2{\rm{ }} + {\rm{ }}1;{\rm{ }}3{\rm{ }} + {\rm{ }}2} \right)\) hay \(B'\left( {3;{\rm{ }}5} \right).\)
Ảnh của điểm C(4; 0) qua phép biến hình f là điểm \(C'\left( {4{\rm{ }} + {\rm{ }}1;{\rm{ }}0{\rm{ }} + {\rm{ }}2} \right)\) hay \(C'\left( {5;{\rm{ }}2} \right).\)
b) Vì \(M\left( {{x_0};{\rm{ }}{y_0}} \right)\) thuộc \(\Delta :{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}4{\rm{ }} = {\rm{ }}0\) nên \({x_0}\; + {\rm{ }}{y_0}\;-{\rm{ }}4{\rm{ }} = {\rm{ }}0\) hay \({x_0}\; + {\rm{ }}{y_{0\;}} = {\rm{ }}4\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow \;{x_0}\; + {\rm{ }}{y_0}\; + {\rm{ }}3{\rm{ }} = {\rm{ }}4{\rm{ }} + {\rm{ }}3}\\{ \Leftrightarrow \;\left( {{x_0}\; + {\rm{ }}1} \right){\rm{ }} + {\rm{ }}\left( {{y_{0\;}} + {\rm{ }}2} \right){\rm{ }} = {\rm{ }}7}\\{ \Leftrightarrow \;\left( {{x_0}\; + {\rm{ }}1} \right){\rm{ }} + {\rm{ }}\left( {{y_{0\;}} + {\rm{ }}2} \right){\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0}\end{array}\)
Suy ra \(M'\left( {{x_0}\; + {\rm{ }}1;{\rm{ }}{y_0}\; + {\rm{ }}2} \right)\) thuộc đường thẳng \(\Delta ':{\rm{ }}x{\rm{ }} + {\rm{ }}y{\rm{ }}-{\rm{ }}7{\rm{ }} = {\rm{ }}0.\)
Quan sát ba tấm ảnh hoa hồng ở Hình 1.4, hãy cho biết hình nào giống ảnh của hình ở giữa qua một phép co về trục.

Phương pháp giải:
Quan sát hình vẽ để trả lời
Lời giải chi tiết:
Quan sát Hình 1.4, ta thấy hình phía bên phải hình ở giữa giống ảnh của hình ở giữa qua một phép co về trục.
Mục 2 của Chuyên đề học tập Toán 11 - Kết nối tri thức tập trung vào các kiến thức về hàm số bậc hai. Đây là một phần quan trọng trong chương trình Toán 11, đòi hỏi học sinh phải nắm vững các khái niệm cơ bản như định nghĩa hàm số bậc hai, đồ thị hàm số bậc hai, các tính chất của hàm số bậc hai, và cách giải các bài toán liên quan.
Các bài tập trên trang 6 chủ yếu xoay quanh việc xác định các hệ số a, b, c của hàm số bậc hai y = ax2 + bx + c, xác định đỉnh, trục đối xứng, và giao điểm với các trục tọa độ. Việc hiểu rõ các yếu tố này là nền tảng để vẽ đồ thị hàm số bậc hai và giải các bài toán liên quan.
Trang 7 tập trung vào việc vẽ đồ thị hàm số bậc hai dựa trên các yếu tố đã xác định ở trang 6. Học sinh cần nắm vững cách xác định các điểm đặc biệt trên đồ thị như đỉnh, giao điểm với trục hoành, giao điểm với trục tung, và sử dụng các điểm này để vẽ đồ thị một cách chính xác.
Các bài tập trên trang 8 yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai để giải các bài toán thực tế, chẳng hạn như tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số, hoặc giải các phương trình bậc hai. Đây là phần quan trọng để đánh giá khả năng áp dụng kiến thức vào thực tế của học sinh.
Bài 6: Tìm giá trị lớn nhất của hàm số y = -x2 + 6x - 5.
Bài 7: Giải phương trình x2 - 5x + 6 = 0.
Để giải các bài tập về hàm số bậc hai một cách hiệu quả, bạn nên:
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết và hướng dẫn từng bước cho tất cả các bài tập trong mục 2 trang 6, 7, 8 Chuyên đề học tập Toán 11 - Kết nối tri thức. Bạn có thể tham khảo lời giải để hiểu rõ hơn về cách giải bài tập và rèn luyện kỹ năng giải toán của mình.
Để học tốt hơn về hàm số bậc hai, bạn có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với những kiến thức và lời giải chi tiết mà chúng tôi cung cấp, bạn sẽ tự tin hơn trong việc giải các bài tập về hàm số bậc hai và đạt kết quả tốt nhất trong học tập. Chúc bạn học tốt!