Bài 3.11 trang 66 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài giải chi tiết dưới đây sẽ cung cấp phương pháp tiếp cận và lời giải chính xác, giúp bạn hiểu rõ hơn về kiến thức đã học.
Giaitoan.edu.vn cung cấp lời giải bài tập Toán 11 Kết nối tri thức đầy đủ, chính xác, giúp bạn tự học hiệu quả và đạt kết quả cao trong các kỳ thi.
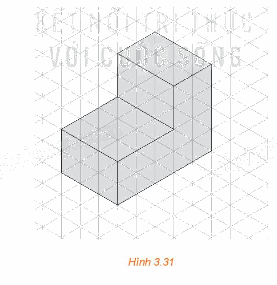
Hình chiếu trục đo của một vật thể được vẽ trên giấy kẻ ô tam giác đều như trong Hình 3.31.
Đề bài
Hình chiếu trục đo của một vật thể được vẽ trên giấy kẻ ô tam giác đều như trong Hình 3.31. Quy ước độ dài mỗi cạnh của tam giác đều là 10 cm, tính thể tích của vật thể đó.
Phương pháp giải - Xem chi tiết
Quan sát hình vẽ để trả lời
Lời giải chi tiết
Chia vật thể thành hai hình hộp chữ nhật A và B (hình vẽ dưới).

Hình hộp chữ nhật A có: Chiều dài đáy 50 cm, chiều rộng đáy 30 cm, chiều cao 20 cm.
Thể tích hình hộp chữ nhật A là: 50 . 30 . 20 = 30 000 (cm3).
Hình hộp chữ nhật B có: Chiều dài đáy 30 cm, chiều rộng đáy 20 cm, chiều cao 20 cm.
Thể tích hình hộp chữ nhật B là: 30 . 20 . 20 = 12 000 (cm3).
Do đó, thể tích vật thể là: 30 000 + 12 000 = 42 000 (cm3).
Bài 3.11 trang 66 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh xét hàm số và tìm các điểm cực trị. Để giải bài này, chúng ta cần nắm vững các bước sau:
Đề bài: Xét hàm số f(x) = x3 - 3x2 + 2.
Lời giải:
f'(x) = 3x2 - 6x
f'(x) = 0 ⇔ 3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy, các điểm dừng là x = 0 và x = 2.
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Lưu ý:
Mở rộng:
Ngoài việc tìm các điểm cực trị, chúng ta còn có thể sử dụng đạo hàm để khảo sát tính đơn điệu, giới hạn và vẽ đồ thị hàm số. Việc nắm vững các kiến thức này sẽ giúp bạn giải quyết các bài toán phức tạp hơn một cách hiệu quả.
Bài tập tương tự:
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự trong sách giáo khoa và các tài liệu tham khảo khác. Hãy chú trọng vào việc hiểu bản chất của bài toán và áp dụng các phương pháp giải phù hợp.
Giaitoan.edu.vn hy vọng với lời giải chi tiết này, bạn đã hiểu rõ cách giải bài 3.11 trang 66 Chuyên đề học tập Toán 11 Kết nối tri thức. Chúc bạn học tập tốt!