Bài 1.18 trang 24 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải chi tiết của bài 1.18 này ngay bây giờ!
Cho một mảnh giấy hình thang cân ABCD (AB // CD). Hãy chỉ ra một cách cắt mảnh giấy đó thành hai mảnh giấy bằng nhau.
Đề bài
Cho một mảnh giấy hình thang cân ABCD (AB // CD). Hãy chỉ ra một cách cắt mảnh giấy đó thành hai mảnh giấy bằng nhau.
Phương pháp giải - Xem chi tiết
Có một đường thẳng chia hình thành hai phần bằng nhau mà nếu “gấp” hình theo đường thẳng thì hai phần đó “chồng khít” lên nhau. Được gọi là hình có trục đối xứng và đường thẳng là trục đối xứng của nó.
Lời giải chi tiết
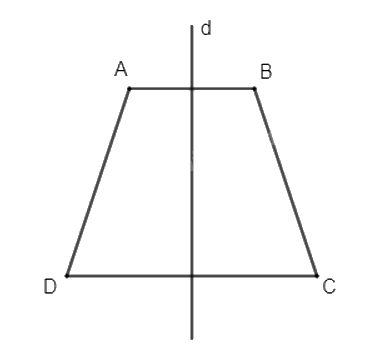
Gọi d là đường trung trực của đoạn thẳng AB. Vì ABCD là hình thang cân có AB // CD nên d cũng là đường trung trực của đoạn thẳng CD.
Khi đó, sử dụng phép đối xứng trục d ta chia hình thang cân ABCD thành 2 hình bằng nhau.
Vậy ta có thể cắt mảnh giấy hình thang cân ABCD theo trục d là đường trung trực của đoạn thẳng AB thì ta được hai mảnh giấy bằng nhau.
Bài 1.18 trang 24 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh giải một bài toán liên quan đến việc tìm đạo hàm và sử dụng đạo hàm để khảo sát hàm số. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về đạo hàm, bao gồm:
Để giải bài 1.18 trang 24 Chuyên đề học tập Toán 11 Kết nối tri thức, chúng ta thực hiện các bước sau:
Giả sử hàm số cần khảo sát là f(x) = x3 - 3x2 + 2. Chúng ta thực hiện các bước sau:
Khi giải bài 1.18 trang 24 Chuyên đề học tập Toán 11 Kết nối tri thức, bạn cần chú ý:
Bài 1.18 trang 24 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm. Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin giải bài toán này một cách hiệu quả.