Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 11 của giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho các bài tập trong Chuyên đề học tập Toán 11 - Kết nối tri thức, đặc biệt là mục 1 trang 35, 36, 37.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Có bốn bạn học sinh khối 11 là An, Bình, Cường và Dung, trong đó: An là bạn của Bình và Cường
Có bốn bạn học sinh khối 11 là An, Bình, Cường và Dung, trong đó: An là bạn của Bình và Cường, nhưng không là bạn của Dung; Dung là bạn của Cường, nhưng không là bạn của Bình; Bình là bạn của Cường.
a) Hãy biểu diễn mỗi bạn An, Bình, Cường, Dung bằng một điểm trên mặt phẳng và dùng chữ cái đầu (in hoa) trong tên của họ để đặt tên cho các điểm này.
b) Nếu hai người là bạn của nhau, hãy nối các điểm biểu diễn tương ứng bằng một đoạn thẳng (hay đoạn đường cong).
c) Từ hình vẽ thu được ở HĐ1b, hãy cho biết: ai có nhiều bạn nhất và ai có ít bạn nhất?
Phương pháp giải:
Vẽ hình theo yêu cầu đề bài
Lời giải chi tiết:
a) Lần lượt biểu diễn mỗi bạn An, Bình, Cường, Dung bằng các điểm A, B, C, D trên mặt phẳng (hình vẽ).
b) Nếu hai người là bạn của nhau, nối các điểm biểu diễn tương ứng (hình vẽ).
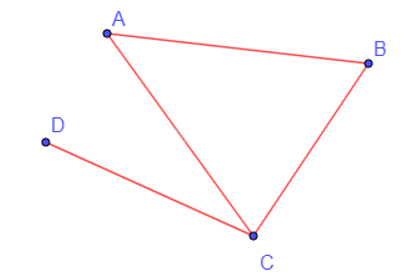
c) Từ hình vẽ thu được, ta thấy Cường có nhiều bạn nhất vì từ điểm C đều có đoạn thẳng nối tới cả 3 điểm A, B, D và Dung có ít bạn nhất vì từ điểm D chỉ có 1 đoạn thẳng nối đến điểm C.
Xét đồ thị nhận được trong Luyện tập 1. Có cặp đỉnh nào của đồ thị này mà không có cạnh nào nối chúng không?
Phương pháp giải:
Quan sát hình vẽ để trả lời
Lời giải chi tiết:
Quan sát đồ thị có được từ Luyện tập 1, ta thấy không có bất kì cặp đỉnh nào của đồ thị mà không có cạnh nối chúng với nhau hay mỗi cặp đỉnh của đồ thị đều được nối với nhau bằng một cạnh.
Vẽ đồ thị G với các đỉnh và các cạnh như sau:
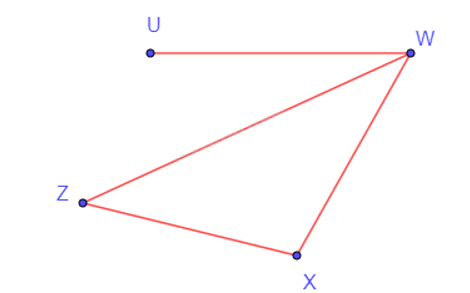
V(G) = {U, W, X, Z} và E(G) = {UW, WX, WZ, XZ}.
G có phải là một đơn đồ thị không?
Phương pháp giải:
Đồ thị G được gọi là đồ thị đơn nếu với mỗi cặp đỉnh của đồ thị chỉ có không quá một cạnh nối chúng và không có đỉnh nào nối với chính nó bởi một cạnh của đồ thị.
Lời giải chi tiết:
G là một đơn đồ thị, do hai đỉnh bất kì đều nối với nhau bởi không quá một cạnh.
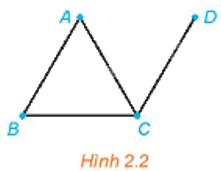
Xét đồ thị cho trong Hình 2.2.
a) Đồ thị trên có khuyên không?
b) Có hai đỉnh nào của đồ thị được nối với nhau bằng nhiều hơn một cạnh không?
Phương pháp giải:
Nếu hai đầu mút của cạnh trùng nhau tại đỉnh M thì ta gọi cạnh ấy là một khuyên, kí hiệu MM.
Lời giải chi tiết:
a) Đồ thị trên không có khuyên vì không có cạnh nào có hai đầu mút trùng nhau tại một đỉnh.
b) Không có hai đỉnh nào của đồ thị được nối với nhau bằng nhiều hơn một cạnh
Vẽ các đồ thị đầy đủ có 5 đỉnh, có 6 đỉnh.
Phương pháp giải:
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết:
+) Đồ thị đầy đủ có 5 đỉnh:
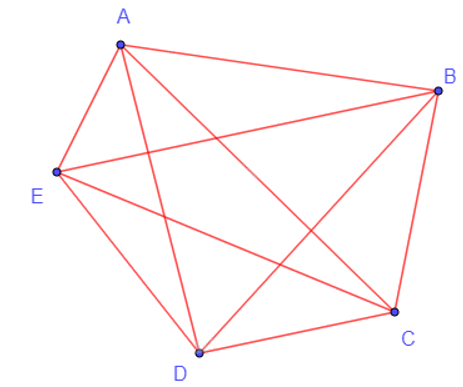
+) Đồ thị đầy đủ có 6 đỉnh:
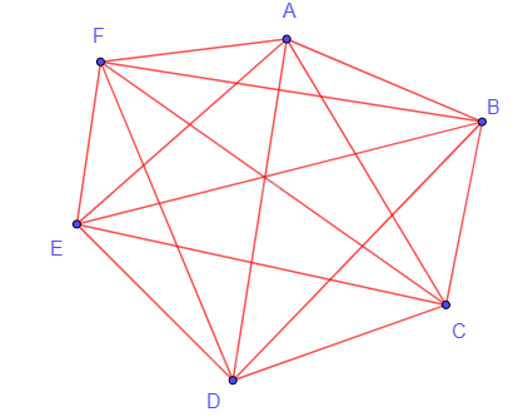
Bảng F của giải vô địch bóng đá thế giới World Cup 2018 gồm bốn đội: Đức, Hàn Quốc, Mexico và Thuỵ Điển. Biểu diễn các đội này bằng các điểm phân biệt kí hiệu lần lượt là D, H, M, T (vẽ sao cho không có ba điểm nào thẳng hàng để dễ quan sát) và nếu hai đội nào đấu với nhau thì ta nối hai điểm tương ứng bằng một đoạn thẳng, ta sẽ được một đồ thị G.
Viết tập hợp các đỉnh và tập hợp các cạnh của đồ thị G.
Phương pháp giải:
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết:
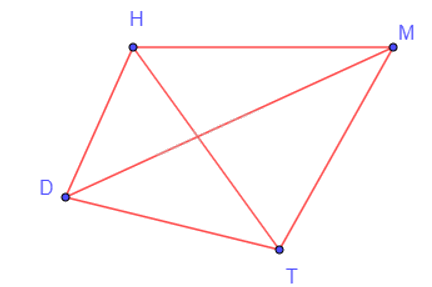
Trong một bảng đấu, các đội sẽ thi đấu vòng tròn, có nghĩa là mỗi một đội sẽ lần lượt thi đấu với ba đội còn lại. Do đó, từ mỗi điểm D, H, M, T, ta vẽ các đoạn thẳng đến các điểm còn lại ta được đồ thị G như hình vẽ dưới đây.
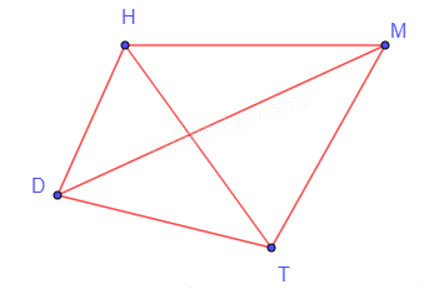
Khi đó ta có: V(G) = {D; H; M; T}.
E(G) = {DH; DT; DM; HT; HM; MT}.
Có bốn bạn học sinh khối 11 là An, Bình, Cường và Dung, trong đó: An là bạn của Bình và Cường, nhưng không là bạn của Dung; Dung là bạn của Cường, nhưng không là bạn của Bình; Bình là bạn của Cường.
a) Hãy biểu diễn mỗi bạn An, Bình, Cường, Dung bằng một điểm trên mặt phẳng và dùng chữ cái đầu (in hoa) trong tên của họ để đặt tên cho các điểm này.
b) Nếu hai người là bạn của nhau, hãy nối các điểm biểu diễn tương ứng bằng một đoạn thẳng (hay đoạn đường cong).
c) Từ hình vẽ thu được ở HĐ1b, hãy cho biết: ai có nhiều bạn nhất và ai có ít bạn nhất?
Phương pháp giải:
Vẽ hình theo yêu cầu đề bài
Lời giải chi tiết:
a) Lần lượt biểu diễn mỗi bạn An, Bình, Cường, Dung bằng các điểm A, B, C, D trên mặt phẳng (hình vẽ).
b) Nếu hai người là bạn của nhau, nối các điểm biểu diễn tương ứng (hình vẽ).
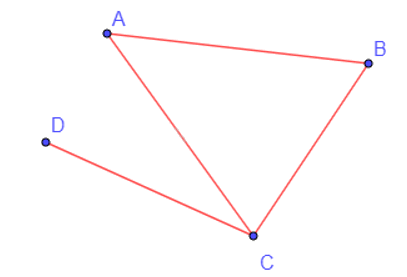
c) Từ hình vẽ thu được, ta thấy Cường có nhiều bạn nhất vì từ điểm C đều có đoạn thẳng nối tới cả 3 điểm A, B, D và Dung có ít bạn nhất vì từ điểm D chỉ có 1 đoạn thẳng nối đến điểm C.
Bảng F của giải vô địch bóng đá thế giới World Cup 2018 gồm bốn đội: Đức, Hàn Quốc, Mexico và Thuỵ Điển. Biểu diễn các đội này bằng các điểm phân biệt kí hiệu lần lượt là D, H, M, T (vẽ sao cho không có ba điểm nào thẳng hàng để dễ quan sát) và nếu hai đội nào đấu với nhau thì ta nối hai điểm tương ứng bằng một đoạn thẳng, ta sẽ được một đồ thị G.
Viết tập hợp các đỉnh và tập hợp các cạnh của đồ thị G.
Phương pháp giải:
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết:
Trong một bảng đấu, các đội sẽ thi đấu vòng tròn, có nghĩa là mỗi một đội sẽ lần lượt thi đấu với ba đội còn lại. Do đó, từ mỗi điểm D, H, M, T, ta vẽ các đoạn thẳng đến các điểm còn lại ta được đồ thị G như hình vẽ dưới đây.
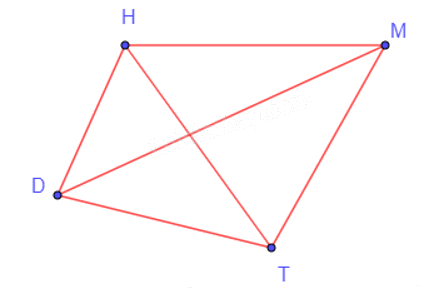
Khi đó ta có: V(G) = {D; H; M; T}.
E(G) = {DH; DT; DM; HT; HM; MT}.
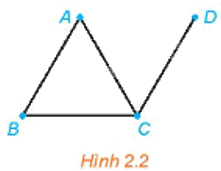
Xét đồ thị cho trong Hình 2.2.
a) Đồ thị trên có khuyên không?
b) Có hai đỉnh nào của đồ thị được nối với nhau bằng nhiều hơn một cạnh không?
Phương pháp giải:
Nếu hai đầu mút của cạnh trùng nhau tại đỉnh M thì ta gọi cạnh ấy là một khuyên, kí hiệu MM.
Lời giải chi tiết:
a) Đồ thị trên không có khuyên vì không có cạnh nào có hai đầu mút trùng nhau tại một đỉnh.
b) Không có hai đỉnh nào của đồ thị được nối với nhau bằng nhiều hơn một cạnh
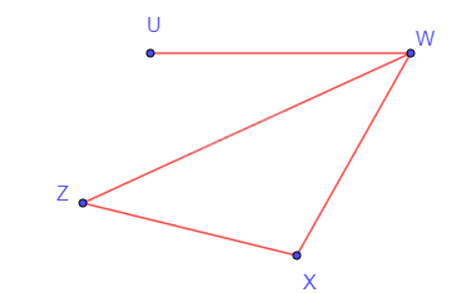
Vẽ đồ thị G với các đỉnh và các cạnh như sau:
V(G) = {U, W, X, Z} và E(G) = {UW, WX, WZ, XZ}.
G có phải là một đơn đồ thị không?
Phương pháp giải:
Đồ thị G được gọi là đồ thị đơn nếu với mỗi cặp đỉnh của đồ thị chỉ có không quá một cạnh nối chúng và không có đỉnh nào nối với chính nó bởi một cạnh của đồ thị.
Lời giải chi tiết:
G là một đơn đồ thị, do hai đỉnh bất kì đều nối với nhau bởi không quá một cạnh.
Xét đồ thị nhận được trong Luyện tập 1. Có cặp đỉnh nào của đồ thị này mà không có cạnh nào nối chúng không?
Phương pháp giải:
Quan sát hình vẽ để trả lời
Lời giải chi tiết:
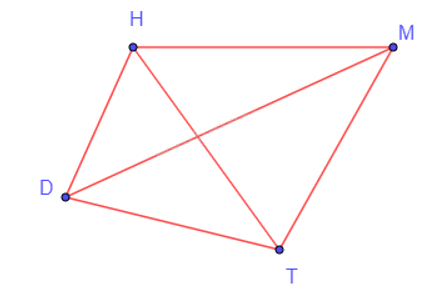
Quan sát đồ thị có được từ Luyện tập 1, ta thấy không có bất kì cặp đỉnh nào của đồ thị mà không có cạnh nối chúng với nhau hay mỗi cặp đỉnh của đồ thị đều được nối với nhau bằng một cạnh.
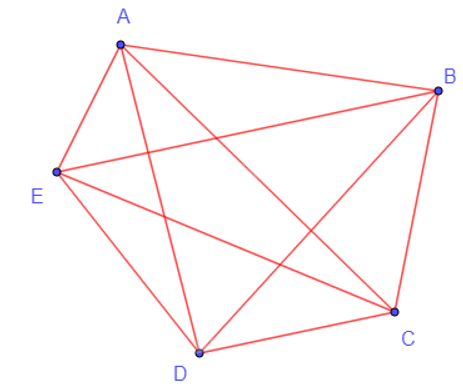
Vẽ các đồ thị đầy đủ có 5 đỉnh, có 6 đỉnh.
Phương pháp giải:
Đồ thị G là hình bao gồm:
- Tập hợp hữu hạn các điểm, mỗi điểm gọi là một đỉnh của đồ thị.
- Tập hợp các đoạn (cong hoặc thẳng), mỗi đoạn nối 2 đỉnh gọi là cạnh của đồ thị.
Lời giải chi tiết:
+) Đồ thị đầy đủ có 5 đỉnh:
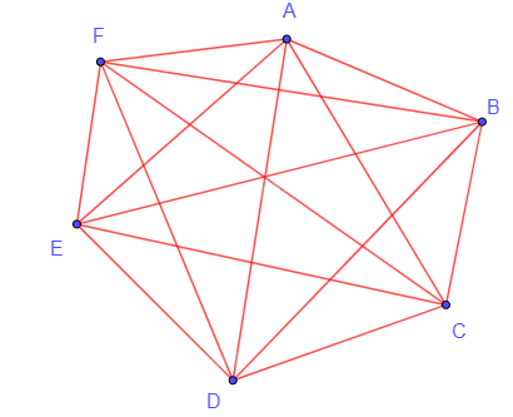
+) Đồ thị đầy đủ có 6 đỉnh:
Mục 1 của Chuyên đề học tập Toán 11 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng linh hoạt các công thức, định lý đã học. Việc giải các bài tập trang 35, 36, 37 là cơ hội để củng cố kiến thức và rèn luyện kỹ năng giải toán. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập, đồng thời phân tích phương pháp giải và những điểm cần lưu ý.
Trước khi đi vào giải bài tập, chúng ta cần nắm vững nội dung chính của Mục 1. Thông thường, mục này sẽ giới thiệu về một khái niệm mới, một định lý quan trọng hoặc một phương pháp giải toán mới. Việc hiểu rõ lý thuyết là nền tảng để giải quyết các bài tập một cách hiệu quả.
Bài tập 1 thường là những bài tập cơ bản, giúp học sinh làm quen với khái niệm mới. Để giải bài tập này, các em cần:
Ví dụ, nếu bài tập yêu cầu tính giá trị của một biểu thức, các em cần thay các giá trị đã cho vào biểu thức và thực hiện các phép tính theo đúng thứ tự ưu tiên.
Bài tập 2 có thể phức tạp hơn bài tập 1, đòi hỏi học sinh phải vận dụng kiến thức đã học một cách linh hoạt. Để giải bài tập này, các em cần:
Ví dụ, nếu bài tập yêu cầu chứng minh một đẳng thức, các em cần biến đổi một vế của đẳng thức để đưa về vế còn lại.
Bài tập 3 thường là những bài tập nâng cao, đòi hỏi học sinh phải có khả năng tư duy và sáng tạo. Để giải bài tập này, các em cần:
Ví dụ, nếu bài tập yêu cầu giải một bài toán thực tế, các em cần xây dựng mô hình toán học và giải mô hình đó.
Để giải bài tập Toán 11 một cách hiệu quả, các em cần lưu ý những điều sau:
Do giới hạn về độ dài, chúng tôi sẽ chỉ cung cấp lời giải chi tiết cho một bài tập minh họa:
Bài tập: Cho hàm số y = x2 - 4x + 3. Tìm tọa độ đỉnh của parabol.
Lời giải:
Hàm số y = x2 - 4x + 3 có dạng y = ax2 + bx + c, với a = 1, b = -4, c = 3.
Tọa độ đỉnh của parabol là:
xđỉnh = -b / (2a) = -(-4) / (2 * 1) = 2
yđỉnh = a * xđỉnh2 + b * xđỉnh + c = 1 * 22 - 4 * 2 + 3 = -1
Vậy, tọa độ đỉnh của parabol là (2; -1).
Việc giải bài tập mục 1 trang 35, 36, 37 Chuyên đề học tập Toán 11 - Kết nối tri thức là một bước quan trọng trong quá trình học tập môn Toán. Hy vọng rằng, với những lời giải chi tiết và phương pháp giải hiệu quả mà chúng tôi cung cấp, các em sẽ tự tin hơn trong việc giải quyết các bài tập và đạt kết quả tốt nhất.