Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 26, 27 Chuyên đề học tập Toán 11 - Kết nối tri thức. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và đạt kết quả tốt trong môn Toán.
Chúng tôi cung cấp các bước giải bài tập rõ ràng, kèm theo giải thích chi tiết để các em có thể tự học và hiểu sâu sắc vấn đề.
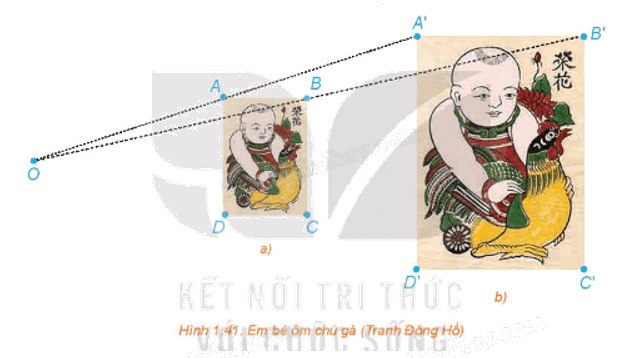
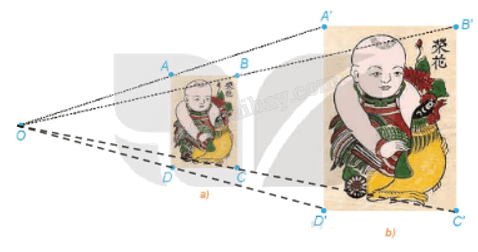
Trong hai bức tranh ở Hình 1.41, các hình chữ nhật ABCD, A'B'C'D' có các cạnh tương ứng song song, bức tranh lớn có kích thước gấp đôi bức tranh nhỏ.
Phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm O thành điểm nào? Nếu phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm M thành điểm M' thì phép vị tự \({V_{\left( {O,\frac{1}{k}} \right)}}\) biến điểm M' thành điểm nào?
Phương pháp giải:
Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết:
- Phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm O thành điểm O.
- Nếu phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm M thành điểm M' thì phép vị tự \({V_{\left( {O,\frac{1}{k}} \right)}}\) biến điểm M' thành điểm M.
Thật vậy, nếu M' là ảnh M qua phép vị tự \({V_{(O,{\rm{ }}k)}}\) thì \(\overrightarrow {OM'} = k\overrightarrow {OM} \Leftrightarrow \overrightarrow {OM} = \frac{1}{k}\overrightarrow {OM'} \). Điều này có nghĩa là M là ảnh của M' qua phép vị tự \({V_{\left( {O,\frac{1}{k}} \right)}}\).
Chứng minh rằng, phép vị tự \({V_{(O,{\rm{ }}1)}}\) là phép đồng nhất, phép vị tự \({V_{\left( {o,-1} \right)}}\;\) là phép đối xứng tâm O.
Phương pháp giải:
Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết:
+ Phép vị tự \({V_{(O,{\rm{ }}1)}}\) biến điểm M thành điểm M' thỏa mãn \(\overrightarrow {OM'} = \overrightarrow {OM} \). Khi đó M' trùng với M. Do đó, phép vị tự \({V_{(O,{\rm{ }}1)}}\) là phép đồng nhất.
+ Phép vị tự \({V_{\left( {o,-1} \right)}}\;\) biến điểm M thành điểm M" thỏa mãn . Khi đó O là trung điểm của MM". Do đó, M" là ảnh của M qua phép đối xứng tâm O hay phép vị tự \({V_{\left( {o,-1} \right)}}\;\) là phép đối xứng tâm O.
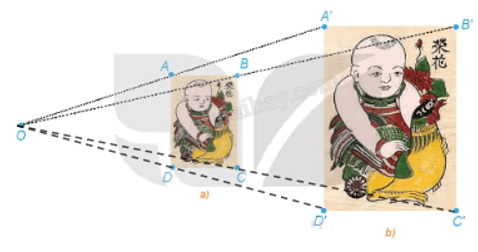
Trong hai bức tranh ở Hình 1.41, các hình chữ nhật ABCD, A'B'C'D' có các cạnh tương ứng song song, bức tranh lớn có kích thước gấp đôi bức tranh nhỏ.
a) Giải thích vì sao các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O.
b) Hãy tính các tỉ số \(\frac{{OA}}{{OA'}},\,\frac{{OB}}{{OB'}},\,\frac{{OC}}{{OC'}},\,\frac{{OD}}{{OD'}}\).
c) Dùng thước thẳng nối hai điểm tương ứng nào đó trên hai bức tranh (chẳng hạn, đầu mỏ trên của chú gà ở hai bức tranh). Đường thẳng đó có đi qua O hay không?
Phương pháp giải:
Dựa vào định lí Thalès để chứng minh A, B, C, D lần lượt là trung điểm của A’O, B’O, C’O, D’O.
Lời giải chi tiết:
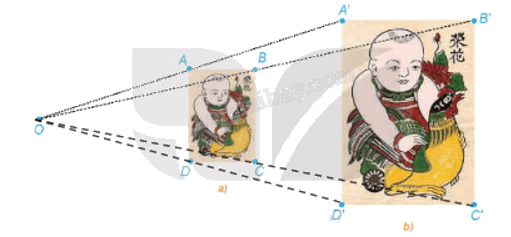
a) Gọi O là giao điểm của AA' và BB'.
Xét tam giác OA'B' có AB // A'B', theo định lý Thales, ta có:
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{2}\)
Từ đó suy ra A, B lần lượt là trung điểm của OA' và OB'.
Gọi C" là giao điểm của BC và OC'. Vì BC // B'C' nên BC" // B'C'.
Xét tam giác OB'C' có BC" // B'C' và B là trung điểm của OB' nên BC" là đường trung bình của tam giác OB'C'. Suy ra và C" là trung điểm của OC'.
Mặt khác theo giả thiết ta có \(BC = \frac{1}{2}B'C'\). Do vậy C" trùng với C và C là trung điểm của OC'.
Chứng minh tương tự, ta được D là trung điểm của OD'.
Vậy các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O.
b) Vì A, B, C, D lần lượt là trung điểm của OA', OB', OC', OD' nên
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{2}\).
c) Dùng thước thẳng nối hai điểm tương ứng trên hai bức tranh, cụ thể, đầu mỏ trên của chú gà ở hai bức tranh, ta thấy đường thẳng này đi qua điểm O.
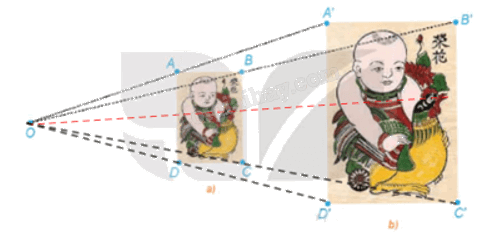
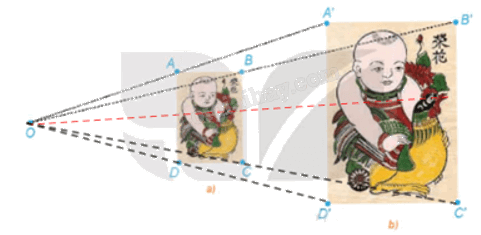
Quan sát hai bức tranh em bé ôm chú gà ở phần mở đầu bài học và chỉ ra phép vị tự biến bức tranh nhỏ thành bức tranh lớn và phép vị tự biến bức tranh lớn thành bức tranh nhỏ.
Phương pháp giải:
Quan sát hình ảnh và tìm tỉ số k
Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết:
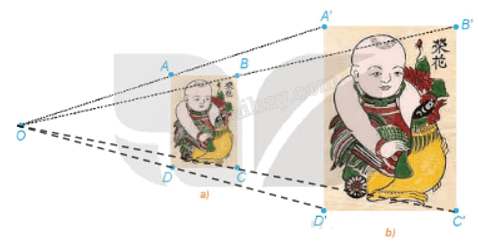
Ta có: \(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{OC}}{{OC'}} = \frac{{OD}}{{OD'}} = \frac{1}{2}\) (theo HĐ1).
Suy ra \(\overrightarrow {OA'} = 2\overrightarrow {OA} ;\,\overrightarrow {OB'} = 2\overrightarrow {OB} ;\,\overrightarrow {OC'} = 2\overrightarrow {OC} ;\,\overrightarrow {OD'} = 2\overrightarrow {OD} \).
Từ đó ta có các điểm A', B', C', D' lần lượt là ảnh của các điểm A, B, C, D qua phép vị tự \({V_{\left( {O,2} \right)}}\). Do đó, phép vị tự V(O, 2) biến hình chữ nhật ABCD thành hình chữ nhật A'B'C'D'.
Vậy phép vị tự \({V_{\left( {O,2} \right)}}\) biến bức tranh nhỏ thành bức tranh lớn. Khi đó, phép vị tự \({V_{\left( {O,\frac{1}{2}} \right)}}\) biến bức tranh lớn thành bức tranh nhỏ.
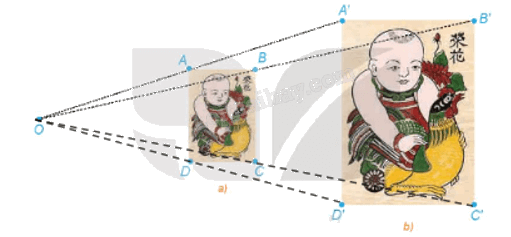
Trong hai bức tranh ở Hình 1.41, các hình chữ nhật ABCD, A'B'C'D' có các cạnh tương ứng song song, bức tranh lớn có kích thước gấp đôi bức tranh nhỏ.
a) Giải thích vì sao các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O.
b) Hãy tính các tỉ số \(\frac{{OA}}{{OA'}},\,\frac{{OB}}{{OB'}},\,\frac{{OC}}{{OC'}},\,\frac{{OD}}{{OD'}}\).
c) Dùng thước thẳng nối hai điểm tương ứng nào đó trên hai bức tranh (chẳng hạn, đầu mỏ trên của chú gà ở hai bức tranh). Đường thẳng đó có đi qua O hay không?
Phương pháp giải:
Dựa vào định lí Thalès để chứng minh A, B, C, D lần lượt là trung điểm của A’O, B’O, C’O, D’O.
Lời giải chi tiết:
a) Gọi O là giao điểm của AA' và BB'.
Xét tam giác OA'B' có AB // A'B', theo định lý Thales, ta có:
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{2}\)
Từ đó suy ra A, B lần lượt là trung điểm của OA' và OB'.
Gọi C" là giao điểm của BC và OC'. Vì BC // B'C' nên BC" // B'C'.
Xét tam giác OB'C' có BC" // B'C' và B là trung điểm của OB' nên BC" là đường trung bình của tam giác OB'C'. Suy ra và C" là trung điểm của OC'.
Mặt khác theo giả thiết ta có \(BC = \frac{1}{2}B'C'\). Do vậy C" trùng với C và C là trung điểm của OC'.
Chứng minh tương tự, ta được D là trung điểm của OD'.
Vậy các đường thẳng AA', BB', CC', DD' cùng đi qua một điểm O.
b) Vì A, B, C, D lần lượt là trung điểm của OA', OB', OC', OD' nên
\(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{AB}}{{A'B'}} = \frac{1}{2}\).
c) Dùng thước thẳng nối hai điểm tương ứng trên hai bức tranh, cụ thể, đầu mỏ trên của chú gà ở hai bức tranh, ta thấy đường thẳng này đi qua điểm O.
Phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm O thành điểm nào? Nếu phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm M thành điểm M' thì phép vị tự \({V_{\left( {O,\frac{1}{k}} \right)}}\) biến điểm M' thành điểm nào?
Phương pháp giải:
Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết:
- Phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm O thành điểm O.
- Nếu phép vị tự \({V_{(O,{\rm{ }}k)}}\) biến điểm M thành điểm M' thì phép vị tự \({V_{\left( {O,\frac{1}{k}} \right)}}\) biến điểm M' thành điểm M.
Thật vậy, nếu M' là ảnh M qua phép vị tự \({V_{(O,{\rm{ }}k)}}\) thì \(\overrightarrow {OM'} = k\overrightarrow {OM} \Leftrightarrow \overrightarrow {OM} = \frac{1}{k}\overrightarrow {OM'} \). Điều này có nghĩa là M là ảnh của M' qua phép vị tự \({V_{\left( {O,\frac{1}{k}} \right)}}\).
Chứng minh rằng, phép vị tự \({V_{(O,{\rm{ }}1)}}\) là phép đồng nhất, phép vị tự \({V_{\left( {o,-1} \right)}}\;\) là phép đối xứng tâm O.
Phương pháp giải:
Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết:
+ Phép vị tự \({V_{(O,{\rm{ }}1)}}\) biến điểm M thành điểm M' thỏa mãn \(\overrightarrow {OM'} = \overrightarrow {OM} \). Khi đó M' trùng với M. Do đó, phép vị tự \({V_{(O,{\rm{ }}1)}}\) là phép đồng nhất.
+ Phép vị tự \({V_{\left( {o,-1} \right)}}\;\) biến điểm M thành điểm M" thỏa mãn . Khi đó O là trung điểm của MM". Do đó, M" là ảnh của M qua phép đối xứng tâm O hay phép vị tự \({V_{\left( {o,-1} \right)}}\;\) là phép đối xứng tâm O.
Quan sát hai bức tranh em bé ôm chú gà ở phần mở đầu bài học và chỉ ra phép vị tự biến bức tranh nhỏ thành bức tranh lớn và phép vị tự biến bức tranh lớn thành bức tranh nhỏ.
Phương pháp giải:
Quan sát hình ảnh và tìm tỉ số k
Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết:
Ta có: \(\frac{{OA}}{{OA'}} = \frac{{OB}}{{OB'}} = \frac{{OC}}{{OC'}} = \frac{{OD}}{{OD'}} = \frac{1}{2}\) (theo HĐ1).
Suy ra \(\overrightarrow {OA'} = 2\overrightarrow {OA} ;\,\overrightarrow {OB'} = 2\overrightarrow {OB} ;\,\overrightarrow {OC'} = 2\overrightarrow {OC} ;\,\overrightarrow {OD'} = 2\overrightarrow {OD} \).
Từ đó ta có các điểm A', B', C', D' lần lượt là ảnh của các điểm A, B, C, D qua phép vị tự \({V_{\left( {O,2} \right)}}\). Do đó, phép vị tự V(O, 2) biến hình chữ nhật ABCD thành hình chữ nhật A'B'C'D'.
Vậy phép vị tự \({V_{\left( {O,2} \right)}}\) biến bức tranh nhỏ thành bức tranh lớn. Khi đó, phép vị tự \({V_{\left( {O,\frac{1}{2}} \right)}}\) biến bức tranh lớn thành bức tranh nhỏ.
Mục 1 trang 26, 27 trong Chuyên đề học tập Toán 11 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và kỹ năng giải bài tập liên quan. Việc giải các bài tập trong mục này không chỉ giúp học sinh củng cố kiến thức mà còn rèn luyện tư duy logic và khả năng áp dụng kiến thức vào thực tế.
Để hiểu rõ hơn về Mục 1 trang 26, 27, chúng ta cần xem xét các nội dung chính sau:
Đề bài: (Giả định một bài tập cụ thể từ trang 26, 27)
Lời giải:
Đề bài: (Giả định một bài tập cụ thể từ trang 26, 27)
Lời giải: (Giải chi tiết tương tự như Bài 1)
Đề bài: (Giả định một bài tập cụ thể từ trang 26, 27)
Lời giải: (Giải chi tiết tương tự như Bài 1)
Để giải các bài tập trong Mục 1 trang 26, 27 một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
Kiến thức và kỹ năng thu được từ việc giải Mục 1 trang 26, 27 có thể được ứng dụng trong nhiều lĩnh vực khác nhau, chẳng hạn như:
Việc giải Mục 1 trang 26, 27 Chuyên đề học tập Toán 11 - Kết nối tri thức là một bước quan trọng trong quá trình học tập môn Toán. Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập hiệu quả mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc chinh phục môn Toán.
| Bài tập | Độ khó | Lời giải |
|---|---|---|
| Bài 1 | Dễ | Xem chi tiết ở trên |
| Bài 2 | Trung bình | Xem chi tiết ở trên |
| Bài 3 | Khó | Xem chi tiết ở trên |