Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Trong bài viết này, chúng tôi sẽ cùng bạn giải quyết các bài tập trong mục 1 trang 30, 31 của Chuyên đề học tập Toán 11 - Kết nối tri thức.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Hai tấm ảnh Dinh Thống Nhất ở hình trên giống nhau về hình dạng, chỉ khác nhau về kích thước.
Phép dời hình và phép vị tự tỉ số t có phải là các phép đồng dạng hay không? Nếu có thì tỉ số đồng dạng là bao nhiêu?
Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:
+ Phép dời hình cũng là phép đồng dạng với tỉ số k = 1.
Thật vậy, ta chứng minh như sau:
Cho hai điểm M, N bất kì và ảnh M', N' tương ứng của nó qua phép dời hình. Khi đó M'N' = MN (phép dời hình bảo toàn khoảng cách giữa hai điểm bất kì). Do đó, M', N' là ảnh của hai điểm M, N bất kì qua phép đồng dạng tỉ số 1.
+ Phép vị tự với tỉ số k là phép đồng dạng với tỉ số đồng dạng \(\left| k \right|\).
Thật vậy, ta chứng minh như sau:
Cho hai điểm M, N bất kì và ảnh M', N' tương ứng của nó qua phép vị tự tỉ số k. Khi đó \(\overrightarrow {M'N'} = k\overrightarrow {MN} \). Do đó, M', N' là ảnh của hai điểm M, N bất kì qua phép đồng dạng tỉ số \(\left| k \right|{\rm{ }}\left( {\left| k \right| > 0} \right).\)
Chứng minh rằng phép biến hình có được bằng cách thực hiện liên tiếp phép đồng dạng f với tỉ số k1 và phép đồng dạng g với tỉ số k2 là một phép đồng dạng với tỉ số k1.k2.
Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:
Lấy hai điểm M, N bất kì. Gọi M', N' tương ứng là ảnh của M, N qua phép đồng dạng f với tỉ số k1 thì ta có M'N' = k1MN.
Gọi M", N" tương ứng là ảnh của M', N' qua phép đồng dạng g với tỉ số k2 thì ta có M"N" = k2M'N'.
Khi đó ta có M"N" = k2 M'N' = k2 . (k1MN) = (k1.k2)MN.
Do đó, M", N" tương ứng là ảnh của M, N qua phép đồng dạng với tỉ số k1.k2.
Từ đó suy ra điều phải chứng minh.
Hai tấm ảnh Dinh Thống Nhất ở hình trên giống nhau về hình dạng, chỉ khác nhau về kích thước.
a) Hãy đo và cho biết chiều dài, chiều rộng của tấm ảnh lớn tương ứng gấp mấy lần chiều dài, chiều rộng của tấm ảnh nhỏ.
b) Nếu lấy hai vị trí A, B bất kì thuộc tấm ảnh nhỏ và các vị trí A', B' tương ứng với chúng trên tấm ảnh lớn thì khoảng cách giữa A' và B' gấp mấy lần khoảng cách giữa A và B? Hãy lấy ví dụ cụ thể các vị trí và đo để kiểm tra câu trả lời của bạn.
Phương pháp giải:
Quan sát hình ảnh Dinh Thống Nhất để làm
Lời giải chi tiết:
a) Qua đo đạc, ta thấy chiều dài và chiều rộng của tấm ảnh lớn tương ứng gấp 2 lần chiều dài và chiều rộng của tấm ảnh nhỏ.
b) Lấy các điểm A, B và A', B' tương ứng như hình vẽ.
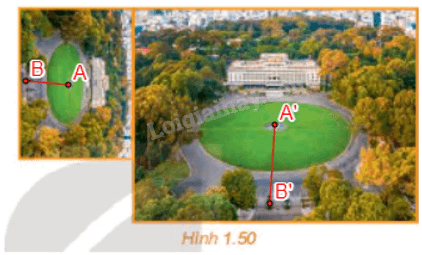
Qua đo đạc ta thấy A'B' = 2AB.
Cho đường thẳng d và hai điểm phân biệt A, B. Điểm M thay đổi trên đường thẳng d. Gọi N là điểm đối xứng của M qua đường thẳng AB và P là trung điểm của đoạn thẳng BN. Chứng minh rằng P thuộc một đường thẳng cố định.
Phương pháp giải:
Dựa vào kiến thức phép đối xứng, phép vị tự để trả lời
Lời giải chi tiết:
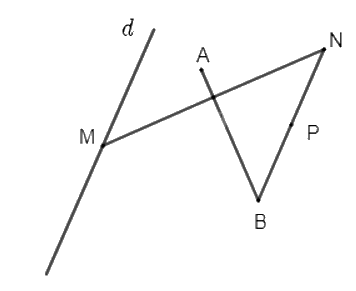
Vì N là điểm đối xứng của M qua đường thẳng AB nên ta có phép đối xứng trục AB biến điểm M thành điểm N.
Ta có P là trung điểm của BN nên \(\overrightarrow {BP} = \frac{1}{2}\overrightarrow {BN} \), do đó ta có phép vị tự tâm B, tỉ số \(\frac{1}{2}\) biến điểm N thành điểm P.
Như vậy, phép đồng dạng có được bằng các thực hiện liên tiếp phép đối xứng trục AB và phép vị tự \({V_{\left( {B,\frac{1}{2}} \right)}}\)biến điểm M thành điểm P.
Mặt khác M thuộc đường thẳng d cố định, A và B cố định, do đó P thuộc đường thẳng d' cố định là ảnh của đường thẳng d qua phép đồng dạng có được bằng các thực hiện liên tiếp phép đối xứng trục AB và phép vị tự \({V_{\left( {B,\frac{1}{2}} \right)}}\).
Vậy P thuộc một đường thẳng cố định.
Trong hai hình Dinh Thống Nhất ở Hình 1.50, hãy chỉ ra phép đồng dạng biến hình nhỏ thành hình lớn.

Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:

Phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc quay 90° và phép vị tự tâm O, tỉ số 2 biến hình Dinh Thống Nhất nhỏ thành hình Dinh Thống Nhất lớn với O là điểm trên hình vẽ.
Hai tấm ảnh Dinh Thống Nhất ở hình trên giống nhau về hình dạng, chỉ khác nhau về kích thước.
a) Hãy đo và cho biết chiều dài, chiều rộng của tấm ảnh lớn tương ứng gấp mấy lần chiều dài, chiều rộng của tấm ảnh nhỏ.
b) Nếu lấy hai vị trí A, B bất kì thuộc tấm ảnh nhỏ và các vị trí A', B' tương ứng với chúng trên tấm ảnh lớn thì khoảng cách giữa A' và B' gấp mấy lần khoảng cách giữa A và B? Hãy lấy ví dụ cụ thể các vị trí và đo để kiểm tra câu trả lời của bạn.
Phương pháp giải:
Quan sát hình ảnh Dinh Thống Nhất để làm
Lời giải chi tiết:
a) Qua đo đạc, ta thấy chiều dài và chiều rộng của tấm ảnh lớn tương ứng gấp 2 lần chiều dài và chiều rộng của tấm ảnh nhỏ.
b) Lấy các điểm A, B và A', B' tương ứng như hình vẽ.

Qua đo đạc ta thấy A'B' = 2AB.
Phép dời hình và phép vị tự tỉ số t có phải là các phép đồng dạng hay không? Nếu có thì tỉ số đồng dạng là bao nhiêu?
Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:
+ Phép dời hình cũng là phép đồng dạng với tỉ số k = 1.
Thật vậy, ta chứng minh như sau:
Cho hai điểm M, N bất kì và ảnh M', N' tương ứng của nó qua phép dời hình. Khi đó M'N' = MN (phép dời hình bảo toàn khoảng cách giữa hai điểm bất kì). Do đó, M', N' là ảnh của hai điểm M, N bất kì qua phép đồng dạng tỉ số 1.
+ Phép vị tự với tỉ số k là phép đồng dạng với tỉ số đồng dạng \(\left| k \right|\).
Thật vậy, ta chứng minh như sau:
Cho hai điểm M, N bất kì và ảnh M', N' tương ứng của nó qua phép vị tự tỉ số k. Khi đó \(\overrightarrow {M'N'} = k\overrightarrow {MN} \). Do đó, M', N' là ảnh của hai điểm M, N bất kì qua phép đồng dạng tỉ số \(\left| k \right|{\rm{ }}\left( {\left| k \right| > 0} \right).\)
Chứng minh rằng phép biến hình có được bằng cách thực hiện liên tiếp phép đồng dạng f với tỉ số k1 và phép đồng dạng g với tỉ số k2 là một phép đồng dạng với tỉ số k1.k2.
Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:
Lấy hai điểm M, N bất kì. Gọi M', N' tương ứng là ảnh của M, N qua phép đồng dạng f với tỉ số k1 thì ta có M'N' = k1MN.
Gọi M", N" tương ứng là ảnh của M', N' qua phép đồng dạng g với tỉ số k2 thì ta có M"N" = k2M'N'.
Khi đó ta có M"N" = k2 M'N' = k2 . (k1MN) = (k1.k2)MN.
Do đó, M", N" tương ứng là ảnh của M, N qua phép đồng dạng với tỉ số k1.k2.
Từ đó suy ra điều phải chứng minh.
Cho đường thẳng d và hai điểm phân biệt A, B. Điểm M thay đổi trên đường thẳng d. Gọi N là điểm đối xứng của M qua đường thẳng AB và P là trung điểm của đoạn thẳng BN. Chứng minh rằng P thuộc một đường thẳng cố định.
Phương pháp giải:
Dựa vào kiến thức phép đối xứng, phép vị tự để trả lời
Lời giải chi tiết:

Vì N là điểm đối xứng của M qua đường thẳng AB nên ta có phép đối xứng trục AB biến điểm M thành điểm N.
Ta có P là trung điểm của BN nên \(\overrightarrow {BP} = \frac{1}{2}\overrightarrow {BN} \), do đó ta có phép vị tự tâm B, tỉ số \(\frac{1}{2}\) biến điểm N thành điểm P.
Như vậy, phép đồng dạng có được bằng các thực hiện liên tiếp phép đối xứng trục AB và phép vị tự \({V_{\left( {B,\frac{1}{2}} \right)}}\)biến điểm M thành điểm P.
Mặt khác M thuộc đường thẳng d cố định, A và B cố định, do đó P thuộc đường thẳng d' cố định là ảnh của đường thẳng d qua phép đồng dạng có được bằng các thực hiện liên tiếp phép đối xứng trục AB và phép vị tự \({V_{\left( {B,\frac{1}{2}} \right)}}\).
Vậy P thuộc một đường thẳng cố định.
Trong hai hình Dinh Thống Nhất ở Hình 1.50, hãy chỉ ra phép đồng dạng biến hình nhỏ thành hình lớn.

Phương pháp giải:
Phép biến hình f gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm bất kì M, N có ảnh lần lượt là M’, N’ ta có: \(M'N' = k.MN\)
Lời giải chi tiết:

Phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc quay 90° và phép vị tự tâm O, tỉ số 2 biến hình Dinh Thống Nhất nhỏ thành hình Dinh Thống Nhất lớn với O là điểm trên hình vẽ.
Mục 1 của Chuyên đề học tập Toán 11 - Kết nối tri thức thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và áp dụng vào giải quyết các bài toán thực tế. Việc giải các bài tập trang 30, 31 là bước quan trọng để củng cố kiến thức và đánh giá khả năng hiểu bài của học sinh.
Để giải quyết hiệu quả các bài tập trong mục này, trước tiên học sinh cần nắm vững các kiến thức sau:
Đề bài: (Giả định một bài tập cụ thể)
Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng và kết luận)
Đề bài: (Giả định một bài tập cụ thể)
Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng và kết luận)
Đề bài: (Giả định một bài tập cụ thể)
Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng và kết luận)
Đề bài: (Giả định một bài tập cụ thể)
Lời giải: (Giải chi tiết bài tập, bao gồm các bước thực hiện, giải thích rõ ràng và kết luận)
Trong mục 1 này, học sinh có thể gặp các dạng bài tập sau:
Để giải các bài tập Toán 11 một cách hiệu quả, bạn có thể áp dụng các mẹo sau:
Ngoài sách giáo khoa, bạn có thể tham khảo thêm các tài liệu sau để học Toán 11 hiệu quả hơn:
Việc giải các bài tập mục 1 trang 30, 31 Chuyên đề học tập Toán 11 - Kết nối tri thức là một bước quan trọng trong quá trình học tập môn Toán. Hy vọng rằng với những hướng dẫn chi tiết và các mẹo giải toán hiệu quả mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong việc giải quyết các bài tập và đạt kết quả tốt nhất.