Bài 3.19 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài giải chi tiết dưới đây sẽ cung cấp phương pháp giải bài tập hiệu quả và dễ hiểu.
Giaitoan.edu.vn cung cấp lời giải chi tiết, chính xác, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Trong không gian cho điểm A và ba mặt phẳng đôi một vuông góc (P1), (P2) và (P3) giao nhau tại O
Đề bài
Trong không gian cho điểm A và ba mặt phẳng đôi một vuông góc (P1), (P2) và (P3) giao nhau tại O. Gọi A1, A2, A3 lần lượt là hình chiếu vuông góc của A trên các mặt phẳng (P1), (P2) và (P3). Gọi M, N, P lần lượt là chân đường vuông góc hạ từ A xuống các giao tuyến của (P1) và (P2), (P2) và (P3), (P3) và (P1).
a) Chứng minh \(O{A^2}\; = {\rm{ }}O{M^2}\; + {\rm{ }}O{N^2}\; + {\rm{ }}O{P^2}.\)
b) Áp dụng ý a để chứng minh \(OA = \sqrt {\frac{{OA_1^2 + OA_2^2 + OA_3^2}}{2}} \)
Sử dụng kết quả trên để tính độ dài của một đoạn thẳng mà ba hình chiếu có độ dài lần lượt là 1 cm, 2 cm và 3 cm.
Phương pháp giải - Xem chi tiết
Vẽ hình và sử dụng định lý Pytago để làm
Lời giải chi tiết
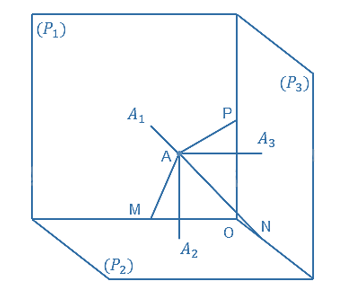
a) Áp dụng định lí Pythagore cho các tam giác vuông.
Tam giác OMA vuông tại M có: OA2 = OM2 + AM2 (1)
Tam giác ONA vuông tại N có: OA2 = ON2 + AN2 (2)
Tam giác OPA vuông tại P có: OA2 = OP2 + AP2 (3)
Cộng vế theo vế của (1), (2), (3) ta được:
3OA2 = (OM2 + ON2 + OP2) + (AM2 + AN2 + AP2)
Ta chứng minh được: AM2 + AN2 + AP2 = 2OA2. (4)
Suy ra: OA2 = OM2 + ON2 + OP2.
b) Vì AM vuông góc OM, OM // AA3 nên AM vuông góc AA3
Mà AA3 vuông góc với OA3
Suy ra: AM // OA3 và AA3 // OM nên AMOA3 là hình bình hành.
Do đó: AM = OA3.
Chứng minh tương tự ta được: AN = OA1, AP = OA2.
Thay kết quả trên vào (4) ta được: \(OA_3^2 + OA_2^2 + OA_1^2 = 2O{A_2}\).
Suy ra \(OA = \sqrt {\frac{{OA_1^2 + OA_2^2 + OA_3^2}}{2}} \).
Ba hình chiếu có độ dài lần lượt là 1 cm, 2 cm và 3 cm.
Thay số vào kết quả trên ta được: \(OA = \sqrt {\frac{{{1^2} + {2^2} + {3^2}}}{2}} = \sqrt 7 \) (cm).
Bài 3.19 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh xét hàm số f(x) = x3 - 3x2 + 2 và thực hiện các yêu cầu sau:
Ta có: f(x) = x3 - 3x2 + 2
Suy ra: f'(x) = 3x2 - 6x
Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:
3x2 - 6x = 0
⇔ 3x(x - 2) = 0
⇔ x = 0 hoặc x = 2
Ta có bảng xét dấu f'(x):
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | NB | ĐC | NC |
Vậy hàm số đạt cực đại tại x = 0, f(0) = 2 và đạt cực tiểu tại x = 2, f(2) = -2.
Hàm số f(x) = x3 - 3x2 + 2 có:
Từ đó, ta có thể kết luận về sự biến thiên của hàm số:
Dựa vào kết quả khảo sát, ta có thể vẽ đồ thị của hàm số f(x) = x3 - 3x2 + 2. Đồ thị đi qua các điểm quan trọng như (0; 2), (2; -2) và có tính chất đồng biến, nghịch biến như đã phân tích.
Bài giải chi tiết trên đã cung cấp cho học sinh phương pháp giải bài 3.19 trang 80 Chuyên đề học tập Toán 11 Kết nối tri thức một cách hiệu quả. Việc nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm là rất quan trọng để giải quyết các bài toán tương tự trong chương trình học.
Hy vọng với lời giải này, các em học sinh sẽ hiểu rõ hơn về bài toán và tự tin hơn trong quá trình học tập môn Toán.