Giải bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức

Bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về dãy số, cấp số cộng và cấp số nhân. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức lý thuyết và áp dụng linh hoạt vào giải quyết các bài toán thực tế.

Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài 1.12 trang 20, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

Cho hình vuông ABCD có tâm O. Trên đường tròn ngoại tiếp hình vuông, theo chiều dương (ngược chiều kim đồng hồ)

Đề bài

Cho hình vuông ABCD có tâm O. Trên đường tròn ngoại tiếp hình vuông, theo chiều dương (ngược chiều kim đồng hồ), thứ tự các đỉnh hình vuông là A, B, C, D.

a) Tìm ảnh của các điểm A, B, C, D qua phép quay tâm O góc quay \(\;\frac{\pi }{2}\).

b) Mỗi phép quay \({Q_{(O,{\rm{ }}o)}},\)\({Q_{\left( {O,\,\frac{\pi }{2}} \right)}},\,{Q_{\left( {O,\,\pi } \right)}},\,{Q_{\left( {O,\,\frac{{3\pi }}{2}} \right)}}\) biến hình vuông ABCD thành hình nào?

Phương pháp giải - Xem chi tiết Giải bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức 1

Vẽ hình, dựa vào định nghĩa: Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\varphi \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \varphi \) được gọi là phép quay tâm O với góc quay \(\varphi \), kí hiệu \({Q_{\left( {O,\varphi } \right)}}\). O gọi là tâm quay, \(\varphi \) gọi là góc quay.

Lời giải chi tiết

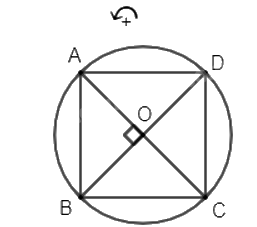
Giải bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức 2

a) Vì ABCD là hình vuông nên hai đường chéo AC và BD vuông góc với nhau tại tâm O và OA = OB = OC = OD.

Khi đó, phép quay \({Q_{\left( {O,\,\frac{\pi }{2}} \right)}}\) biến các điểm A, B, C, D tương ứng thành các điểm B, C, D, A.

b) Phép quay \({Q_{(O,{\rm{ }}o)}}\) biến hình vuông ABCD thành hình vuông ABCD.

Từ câu a, suy ra phép quay \({Q_{\left( {O,\,\frac{\pi }{2}} \right)}}\) biến hình vuông ABCD thành hình vuông BCDA.

Phép quay \({Q_{\left( {O,\,\pi } \right)}}\) biến các điểm A, B, C, D tương ứng thành các điểm C, D, A, B. Do đó phép quay Q_{(O, π)}biến hình vuông ABCD thành hình vuông CDAB.

Phép quay \({Q_{\left( {O,\,\frac{{3\pi }}{2}} \right)}}\) biến các điểm A, B, C, D tương ứng thành các điểm D, A, B, C. Do đó phép quay \({Q_{\left( {O,\,\frac{{3\pi }}{2}} \right)}}\) biến hình vuông ABCD thành hình vuông DABC.

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức – hành trang không thể thiếu trong chuyên mục Giải bài tập Toán 11 trên nền tảng tài liệu toán. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức: Hướng dẫn chi tiết và lời giải

Bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh tìm hiểu về dãy số và các tính chất của nó. Để giải bài tập này một cách hiệu quả, trước hết chúng ta cần nắm vững các khái niệm cơ bản như dãy số, số hạng tổng quát, cấp số cộng, cấp số nhân và các công thức liên quan.

I. Tóm tắt lý thuyết cần nắm vững

Dãy số: Một dãy số là một hàm số được xác định trên tập hợp các số tự nhiên hoặc một tập con của nó.
Số hạng tổng quát: Số hạng thứ n của dãy số, ký hiệu là u_n.
Cấp số cộng: Dãy số mà mỗi số hạng sau đều lớn hơn (hoặc nhỏ hơn) số hạng trước một lượng không đổi, gọi là công sai (d). Công thức: u_n = u₁ + (n-1)d
Cấp số nhân: Dãy số mà mỗi số hạng sau đều bằng số hạng trước nhân với một lượng không đổi, gọi là công bội (q). Công thức: u_n = u₁ * q^(n-1)

II. Phân tích đề bài 1.12 trang 20

Đề bài 1.12 thường yêu cầu học sinh xác định xem một dãy số cho trước có phải là cấp số cộng hay cấp số nhân hay không, hoặc tìm số hạng tổng quát của dãy số đó. Đôi khi, đề bài còn yêu cầu tính tổng của một số lượng hữu hạn các số hạng đầu tiên của dãy số.

III. Lời giải chi tiết bài 1.12 trang 20

(Ở đây sẽ là lời giải chi tiết cho bài 1.12, bao gồm các bước giải, giải thích rõ ràng và ví dụ minh họa. Ví dụ, nếu bài toán yêu cầu xác định dãy số là cấp số cộng hay cấp số nhân, cần trình bày cách tính công sai hoặc công bội. Nếu yêu cầu tìm số hạng tổng quát, cần trình bày công thức và cách áp dụng.)

Ví dụ minh họa:

Giả sử đề bài cho dãy số: 2, 6, 18, 54,...

Bước 1: Tính tỉ số giữa hai số hạng liên tiếp: 6/2 = 3; 18/6 = 3; 54/18 = 3
Bước 2: Vì tỉ số giữa hai số hạng liên tiếp là một hằng số (q = 3), nên dãy số này là một cấp số nhân.
Bước 3: Số hạng đầu tiên là u₁ = 2.
Bước 4: Số hạng tổng quát của dãy số là u_n = 2 * 3^(n-1)

IV. Mở rộng và bài tập tương tự

Để củng cố kiến thức về dãy số và cấp số cộng, cấp số nhân, các em có thể tự giải thêm các bài tập tương tự. Hãy chú ý đến việc phân tích đề bài, xác định đúng loại dãy số và áp dụng các công thức phù hợp.

Một số bài tập tương tự:

Tìm số hạng thứ 10 của cấp số cộng có số hạng đầu u₁ = 3 và công sai d = 2.
Tìm số hạng thứ 5 của cấp số nhân có số hạng đầu u₁ = 1 và công bội q = -2.
Tính tổng của 10 số hạng đầu tiên của cấp số cộng có u₁ = 1 và d = 3.

V. Kết luận

Bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về dãy số và các tính chất của nó. Bằng cách nắm vững lý thuyết, phân tích đề bài và áp dụng các công thức phù hợp, các em có thể giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tốt!