Bài 2.20 trang 50 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hãy cùng khám phá lời giải chi tiết của bài tập này ngay dưới đây!
Vẽ đồ thị G = (V, E) với các đỉnh và các cạnh như sau:
Đề bài
Vẽ đồ thị G = (V, E) với các đỉnh và các cạnh như sau:
V = {1; 2; 3; 4; 5; 6; 7; 8} và E = {12; 13; 23; 34; 35; 67; 68; 78}.
Đồ thị này có phải là đơn đồ thị không? Có phải là đồ thị đầy đủ không?
Phương pháp giải - Xem chi tiết
- Một đồ thị không có khuyên, trong đó hai đỉnh được nối bằng nhiều nhất một cạnh (không có hai cạnh nào cùng nối một cặp đỉnh) gọi là một đơn đồ thị.
- Một đồ thị là đầy đủ khi và chỉ khi mỗi cặp đỉnh của nó đều được nối bằng một cạnh.
Lời giải chi tiết
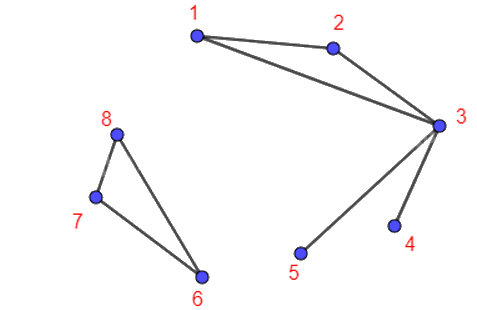
Ta vẽ được đồ thị G như hình trên.
Đồ thị G này không có khuyên và hai đỉnh chỉ được nối với nhau bằng nhiều nhất một cạnh nên là một đơn đồ thị.
Đồ thị G không phải đồ thị đầy đủ vì không phải tất cả các cặp đỉnh của nó đều được nối với nhau bằng một cạnh.
Bài 2.20 trang 50 Chuyên đề học tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết một bài toán thực tế liên quan đến việc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Để giải bài toán này một cách hiệu quả, chúng ta cần thực hiện các bước sau:
Giả sử bài toán yêu cầu tìm giá trị lớn nhất của hàm số f(x) = -x2 + 4x - 3 trên khoảng [0; 3]. Chúng ta sẽ thực hiện các bước sau:
Khi giải các bài tập về đạo hàm, cần lưu ý một số điểm sau:
Bài 2.20 trang 50 Chuyên đề học tập Toán 11 Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm. Hy vọng với hướng dẫn chi tiết và ví dụ minh họa trên, bạn đã có thể tự tin giải quyết bài toán này một cách hiệu quả. Chúc bạn học tập tốt!